Hurwitzquaternion

Eine Hurwitzquaternion (oder Hurwitz-Ganzzahl) in der Mathematik ist eine Quaternion, deren vier Koeffizienten entweder alle (rational-)ganzzahlig oder alle halbzahlig (Hälften ungerader ganzer Zahlen) sind – Mischungen von Ganzzahlen und Halbzahlen sind also unzulässig. Die Menge aller Hurwitzquaternionen ist

$H:=\left\{\xi =x_{0}+x_{1}\,{\mathrm i}+x_{2}\,{\mathrm j}+x_{3}\,{\mathrm k}\;\mid \;(x_{0},x_{1},x_{2},x_{3})\in \mathbb{Z } ^{4}\,\cup \,({\tfrac {1}{2}}+\mathbb{Z } )^{4}\right\}$ .

Sie bildet in ihrem Quotientenkörper, dem Divisionsring (Schiefkörper) der Quaternionen mit rationalen Koeffizienten

$S:=\{\xi =x_{0}+x_{1}\,{\mathrm i}+x_{2}\,{\mathrm j}+x_{3}\,{\mathrm k}\;\mid \;x_{0},x_{1},x_{2},x_{3}\in \mathbb{Q} \}$ ,

eine maximale $\mathbb {Z}$ -Ordnung. ist der kleinste Unterkörper des Quaternionenschiefkörpers $\mathbb {H}$ mit nicht-kommutativer Multiplikation. Andererseits ist seine Vervollständigung (Komplettierung) für die Betrags-Metrik gerade wieder $\mathbb {H}$ .

Eine Lipschitzquaternion (oder Lipschitz-Ganzzahl) ist eine Quaternion, deren Koeffizienten alle ganzzahlig sind. Die Menge aller Lipschitzquaternionen

$L:=\{\xi =x_{0}+x_{1}\,{\mathrm i}+x_{2}\,{\mathrm j}+x_{3}\,{\mathrm k}\;\mid \;x_{0},x_{1},x_{2},x_{3}\in \mathbb{Z } \}$

ist ein (nicht-kommutativer) Unterring von (aber kein Ideal!). und haben denselben Quotientenkörper .

Im Unterschied zu ist maximal als Ganzheitsring und zusätzlich ein euklidischer Ring, d.h., kennt eine Division mit kleinem Rest und einen euklidischen Algorithmus.

Der Artikel behandelt die wichtigsten algebraischen Eigenschaften inklusive Symmetrien von und deren geometrische Auswirkungen. Ferner lässt sich exemplarisch verfolgen, inwieweit Begriffe, die man von den kommutativen Ringen her kennt und die häufig nur dort definiert werden, fürs nicht-kommutative Umfeld angepasst werden können.

Inhaltsverzeichnis

1 Erbschaften
2 Gruppeneigenschaften
- 2.1 Additivität
  - 2.1.1 Lipschitz-Gitter
  - 2.1.2 Hurwitz-Gitter
- 2.2 Multiplikativität
3 Geometrische Eigenschaften
4 Parkettierung und Sphärenpackung
5 Euklidizität
6 Automorphismen
7 Assoziierte Elemente
8 Ideale
9 Prime Elemente, Faktorisierung
10 Metrik, Vervollständigung und Potenzreihenentwicklung
- 10.1 Archimedische Bewertung und Metrik
- 10.2 Nichtarchimedische Bewertung und Metrik
12 Literatur
13 Anmerkungen

Erbschaften

Der Schiefkörper „erbt“ die $\mathrm {i}$ , $\mathrm {j}$ , $\mathrm k$ und alle einschlägigen Rechenregeln von $\mathbb {H}$ , den Quaternionen mit reellen Koeffizienten. Bezüglich der Definitionen wird auf den entsprechenden Artikel verwiesen.

ist ein 4-dimensionaler Vektorraum über seinem Skalarkörper $\mathbb {Q}$ , wie es $\mathbb {H}$ über $\mathbb {R}$ ist. Vom Vektorraum gewinnt man die Addition und die Skalarmultiplikation $\colon \mathbb{Q} \times S\to S$ , bei der der Skalar $r\in \mathbb{Q}$ die Quaternion komponentenweise multipliziert. Diese Multiplikation stimmt in ihrem Definitionsbereich mit der Quaternionen-Multiplikation überein, da als $r+0\,{\mathrm i}+0\,{\mathrm j}+0\,{\mathrm k}$ in die Quaternionen eingebettet wird, und sie ist kommutativ.

In diesem Artikel wird die (volle) Quaternionen-Multiplikation mit dem Mittepunkt $\cdot$ und die Skalarmultiplikation durch einfache Juxtaposition notiert, ferner werden die Quaternionen mit griechischen und die Skalare mit lateinischen Buchstaben geschrieben.

Zur Erläuterung der Auswirkungen der Erbschaften auf das Thema des Artikels seien $\xi =x_{0}+x_{1}\,{\mathrm i}+x_{2}\,{\mathrm j}+x_{3}\,{\mathrm k}$ und $\eta =y_{0}+y_{1}\,{\mathrm i}+y_{2}\,{\mathrm j}+y_{3}\,{\mathrm k}$ beliebige Quaternionen (mit rationalen oder ggf. reellen Koeffizienten).

Das Skalarprodukt $\langle {\cdot },{\cdot }\rangle \colon {\mathbb {H}}\times {\mathbb {H}}\to \mathbb{R}$ , definiert durch

$\langle \xi ,\eta \rangle :=x_{0}y_{0}+x_{1}y_{1}+x_{2}y_{2}+x_{3}y_{3}$ ,
ist eine positiv definite symmetrische Bilinearform. Wir haben die Bilder

$\{\langle \xi ,\eta \rangle \mid \xi ,\eta \in H\}\;=\;{\tfrac {1}{2}}\mathbb{Z }$
und

$\{\langle \xi ,\eta \rangle \mid \xi ,\eta \in L\}\;=\;\mathbb{Z }$
und die Bilder

$\{\langle \xi ,\xi \rangle \mid \xi \in H\}\;=\;\{\langle \xi ,\xi \rangle \mid \xi \in L\}\;=\;\mathbb{N} _{0}$ .
Die Konjugation $\xi \mapsto {\bar \xi }$ wirft $\xi$ nach

${\bar \xi }:=x_{0}-x_{1}\,{\mathrm i}-x_{2}\,{\mathrm j}-x_{3}\,{\mathrm k}$ .
Die Norm, gegeben durch

$\|\xi \|:=\xi \cdot {\bar \xi }={\bar \xi }\cdot \xi =x_{0}^{2}+x_{1}^{2}+x_{2}^{2}+x_{3}^{2}$
ist $=\!\langle \xi ,\xi \rangle =\!|\xi |^{2}$ (Quadrat des Betrags), multiplikativ, rein reell, nicht-negativ und bei einer Hurwitzquaternion immer eine ganze Zahl. Gemäß dem Vier-Quadrate-Satz von Lagrange benötigt man für jede nicht-negative ganze Zahl höchstens 4 Quadratzahlen, deren Summe sie ist. Somit ist jede nicht-negative Ganzzahl Norm einer Lipschitz- (oder Hurwitz-)Quaternion.
Die positive Definitheit des Skalarprodukts bedeutet $\|\xi \|>0$ für $\xi \neq 0$ . Daraus folgt die Existenz des Inversen

$\xi ^{{-1}}={\frac {{\bar \xi }}{\|\xi \|}}\in S$ für $\xi \neq 0$ ,
daraus die Nullteilerfreiheit von .

Gruppeneigenschaften

Folgende Notationen seien in diesem Artikel durchgehalten.

Die Menge

${\mathit {\Lambda }}:=\left\{\xi \in H\mid \|\xi \|\equiv 0\;\operatorname {mod}\,2\right\}$
ist wegen der Multiplikativität der Norm additiv und multiplikativ abgeschlossen und Untermenge von , da alle $\xi$ mit $(x_{0},x_{1},x_{2},x_{3})\in (\mathbb{Z } +{\tfrac {1}{2}})^{4}$ eine ungerade Norm haben. Ferner ist für $\xi \in H$ und $\lambda \in {\mathit {\Lambda }}$ sowohl

$\xi \cdot \lambda \,\in \,{\mathit {\Lambda }}$ als auch $\lambda \cdot \xi \,\in \,{\mathit {\Lambda }}$ .
${\mathit {\Lambda }}$ ist bekannt als das Gitter D₄ im $\mathbb {R} ^{4}$ . Es wird der geraden „Quersummen“ $x_{0}+x_{1}+x_{2}+x_{3}$ wegen auch „Schachbrettgitter“ genannt.
$\xi +{\mathit {\Lambda }}$ .
Die Quaternion

$\varepsilon :={\tfrac {1}{2}}(1+{\mathrm i}+{\mathrm j}+{\mathrm k})$
hat zur 6-ten Potenz, und es ist $\varepsilon ^{2}={\tfrac {1}{2}}(-1+{\mathrm i}+{\mathrm j}+{\mathrm k}),\;\varepsilon ^{3}=-1$ und $\varepsilon ^{4}={\tfrac {1}{2}}(-1-{\mathrm i}-{\mathrm j}-{\mathrm k})$ .
Die Menge

$Q_{4}:=\{0,1,\varepsilon ^{4},\varepsilon ^{2}\}$
ist multiplikativ abgeschlossen.

Additivität

Lipschitz-Gitter

Die additive Gruppe wird erzeugt von $\left\{1,{\mathrm i},{\mathrm j},{\mathrm k}\right\}$ und bildet ein Gitter im $\mathbb {R} ^{4}$ , bekannt als das Gitter I₄.

${\mathit {\Lambda }}$ ist ein Untergitter vom Index 2 von . Es ergeben sich die Partitionen

$L={\color {OliveGreen}[0]}\cup {\color {Red}[1]}$ .

Additionstafel
$\pm$			$[\varepsilon ^{4}]$	$[\varepsilon ^{2}]$
	${\color {OliveGreen}[0]}$	${\color {Red}[1]}$	${\color {OliveGreen}[\varepsilon ^{4}]}$	${\color {Red}[\varepsilon ^{2}]}$
	${\color {Red}[1]}$	${\color {OliveGreen}[0]}$	${\color {Red}[\varepsilon ^{2}]}$	${\color {OliveGreen}[\varepsilon ^{4}]}$
$[\varepsilon ^{4}]$	${\color {OliveGreen}[\varepsilon ^{4}]}$	${\color {Red}[\varepsilon ^{2}]}$	${\color {OliveGreen}[0]}$	${\color {Red}[1]}$
$[\varepsilon ^{2}]$	${\color {Red}[\varepsilon ^{2}]}$	${\color {OliveGreen}[\varepsilon ^{4}]}$	${\color {Red}[1]}$	${\color {OliveGreen}[0]}$

Hurwitz-Gitter

Als additive Gruppe ist frei abelsch mit den Erzeugenden $\left\{\varepsilon ,{\mathrm i},{\mathrm j},{\mathrm k}\right\}$ . bildet ebenfalls ein Gitter im $\mathbb {R} ^{4}$ , bekannt als das Gitter F₄.

ist ein Untergitter vom Index 2 von und es ergeben sich die Partitionen

$H\,=\,L\cup (\varepsilon ^{4}\!+L\!)\,=\,L\cup (\varepsilon ^{2}\!+L\!)\,=\,{\color {OliveGreen}[0]}\cup {\color {Red}[1]}\cup {\color {OliveGreen}[\varepsilon ^{4}]}\cup {\color {Red}[\varepsilon ^{2}]}$

(siehe unten stehendes Diagramm). Damit ist $Q_{4}$ ein vollständiges Repräsentantensystem von $H/{\mathit {\Lambda }}$ .

Die Elemente $\xi$ der Nebenklassen ${\color {OliveGreen}[0]},{\color {OliveGreen}[\varepsilon ^{4}]}$ haben gerade, die von ${\color {Red}[1]},{\color {Red}[\varepsilon ^{2}]}$ ungerade „Quersumme“ $x_{0}+x_{1}+x_{2}+x_{3}$ .

Aus den Nebenklassen des Gitters D₄
gebildete Gitter und Ringe
		${\color {OliveGreen}[0]}\cup {\color {Red}[1]}\cup {\color {OliveGreen}[\varepsilon ^{4}]}\cup {\color {Red}[\varepsilon ^{2}]}$ $=L\cup (\varepsilon ^{4}\!+\!L)$ $=H={\mathsf {F}}_{4}$
	$\diagup$	$\mid$	$\diagdown$
${\color {OliveGreen}[0]}\cup {\color {OliveGreen}[\varepsilon ^{4}]}$ $=\varepsilon ^{4}\!\cdot \!L$		${\color {OliveGreen}[0]}\cup {\color {Red}[1]}$ $=L={\mathsf {I}}_{4}$		${\color {OliveGreen}[0]}\cup {\color {Red}[\varepsilon ^{2}]}$ $=\varepsilon ^{2}\!\cdot \!L$
	$\diagdown$	$\mid$	$\diagup$
		${\color {OliveGreen}[0]}$ $=(\varepsilon ^{4}\!\cdot \!L)\cap L\cap (\varepsilon ^{2}\!\cdot \!L)$ $={\mathit {\Lambda }}={\mathsf {D}}_{4}$

Multiplikativität

Lipschitz-Halbgruppe

Es ist klar, dass das Produkt zweier Lipschitz-Zahlen mit ganzzahligen Koeffizienten wieder ganzzahlige Koeffizienten hat. Somit ist die Menge eine Halbgruppe unter der Quaternionen-Multiplikation $\cdot$ .

Lipschitz-Einheiten

Die Einheitengruppe in ist die nicht-abelsche Quaternionengruppe

${\mathsf {Q}}_{8}:=\left\{\xi \in L\mid \|\xi \|=1\right\}\;=\;\left\{\pm 1,\pm {\mathrm i},\pm {\mathrm j},\pm {\mathrm k}\right\}$

von der Ordnung 8 mit dem Zentrum $Z:=\left\{\pm 1\right\}$ . Erzeugende von Q₈ sind z.B. $\mathrm {i}$ und $\mathrm {j}$ mit den Gleichungen

${\mathrm i}^{4}=1$ , ${\mathrm j}^{2}={\mathrm i}^{2}$ und ${\mathrm j}\cdot {\mathrm i}={\mathrm i}^{3}\cdot {\mathrm j}$ .

Multiplikationstafel
$\cdot$	${\color {White}.}[0]{\color {White}.}$		$[\varepsilon ^{4}]$	$[\varepsilon ^{2}]$
	${\color {OliveGreen}[0]}$	${\color {OliveGreen}[0]}$	${\color {OliveGreen}[0]}$	${\color {OliveGreen}[0]}$
	${\color {OliveGreen}[0]}$	${\color {Red}[1]}$	${\color {OliveGreen}[\varepsilon ^{4}]}$	${\color {Red}[\varepsilon ^{2}]}$
$[\varepsilon ^{4}]$	${\color {OliveGreen}[0]}$	${\color {OliveGreen}[\varepsilon ^{4}]}$	${\color {Red}[\varepsilon ^{2}]}$	${\color {Red}[1]}$
$[\varepsilon ^{2}]$	${\color {OliveGreen}[0]}$	${\color {Red}[\varepsilon ^{2}]}$	${\color {Red}[1]}$	${\color {OliveGreen}[\varepsilon ^{4}]}$

Hurwitz-Halbgruppe

Der Beweis der multiplikativen Abgeschlossenheit von $(H,\cdot )$ gelingt ohne große Rechnerei durch Zusammensetzen aus den 4 Nebenklassen.^{[Anm
1]}

Fazit: Die Mengen und sind abgeschlossen unter der Addition und der Multiplikation $\cdot$ , so dass sie (nicht-kommutative) Unterringe in ihrer beider Quotientenkörper bilden, und ${\mathit {\Lambda }}$ ist ein Ideal in beiden Ringen (siehe auch den Abschnitt Ideale).

Hurwitz-Einheiten

Die Einheitengruppe in , auch Gruppe der Hurwitzeinheiten genannt, ist die nicht-abelsche Gruppe

$Q_{{24}}:=\left\{\xi \in H\mid \|\xi \|=1\right\}$

der Ordnung 24, die aus den 8 Elementen der Gruppe Q₈ und den 16 Quaternionen ${\tfrac {1}{2}}(\pm 1\pm {\mathrm i}\pm {\mathrm j}\pm {\mathrm k})$ besteht, bei denen die Vorzeichen in jeder Kombination zu nehmen sind: den Hurwitzeinheiten im engeren Sinn. $Q_{{24}}$ ist isomorph zur binären Tetraedergruppe 2T, einer zentralen Gruppenerweiterung der Tetraedergruppe T = A₄ von der Ordnung 12 mit einer zyklischen Gruppe der Ordnung 2. Ihr Zentrum ist ebenfalls $Z = \left\{\pm 1 \right\}$ und die Faktorgruppe $Q_{{24}}/Z$ ist isomorph zu A₄.

Q₈ ist Normalteiler vom Index 3 von $Q_{{24}}$ , und $Q_{3}:=\{1,\varepsilon ^{2},\varepsilon ^{4}\}$ ist Untergruppe von $Q_{{24}}$ mit $Q_{3}\cong Q_{{24}}/{\mathsf {Q}}_{8}$ und $Q_{3}\cap {\mathsf {Q}}_{8}=\{1\}$ ; also ist $Q_{{24}}$ das semidirekte Produkt ${\mathsf {Q}}_{8}\rtimes Q_{3}$ .^{[Anm
2]}

Erzeugende von $Q_{{24}}$ sind z.B.

$\varepsilon ={\tfrac {1}{2}}(1+{\mathrm i}+{\mathrm j}+{\mathrm k})$ und $\zeta :={\tfrac {1}{2}}(1+{\mathrm i}+{\mathrm j}-{\mathrm k})$

mit den Gleichungen

$\varepsilon ^{3}=\zeta ^{3}=(\varepsilon \cdot \zeta )^{2}$ ,

wobei $\varepsilon \cdot \zeta =\mathrm {j}$ .

Geometrische Eigenschaften

Regulärer 16-Zeller (Hexadekachor)

3D-Projektion des regulären 16-Zellers

Die Elemente der Gruppe Q₈ haben alle die Norm 1 und bilden die Ecken des Kreuzpolytops der vierten Dimension, des regulären sogenannten 16-Zellers, auch Hexadekachōr(on) (das, englisch hexadecachoron, von griechisch ἑξαδεκάχωρον aus hexa ‚sechs‘ und deka ‚zehn‘ und chōros ‚Raum‘) genannt. Er ist eingeschrieben in die Einheits-3-Sphäre, die selbst wieder eine Gruppe ist, nämlich die Lie-Gruppe SU(2). Sein Rand besteht aus 16 Tetraedern mit den Eckenmengen $\{\pm 1,\pm {\mathrm i},\pm {\mathrm j},\pm {\mathrm k}\}$ , wobei jede der 16 Vorzeichenkombinationen für ein Tetraeder steht. Die Mittelpunkte dieser Tetraeder sind gerade die Hälften der Hurwitzeinheiten im engeren Sinn.

Der 16-Zeller ist zum 8-Zeller dual, gehört zu den 6 regulären konvexen 4-Polytopen (Polychora im $\mathbb {R} ^{4}$ ), hat Schläfli-Symbol {3,3,4} und ist berandet von 16 (regulären) Tetraeder-Zellen, 32 (regulären) Dreiecksflächen, 24 Kanten und 8 Ecken. Sein 4-Volumen ist ${\tfrac {2}{3}}$ bei einer Kantenlänge von ${\sqrt {2}}$ und einem Umkreisradius von 1.

Regulärer 8-Zeller (Tesserakt)

3D-Projektion des regulären 8-Zellers

Die restlichen 16 Elemente $\in Q_{{24}}\!\setminus \!{\mathsf {Q}}_{8}$ , d.s. die Hurwitzeinheiten im engeren Sinn, haben ebenfalls die Norm 1 und bilden die Ecken des Hyperwürfels (Maßpolytops) der vierten Dimension, des regulären sogenannten 8-Zellers, auch Tesserakt genannt. Er ist berandet durch 8 Würfel, einer davon hat bspw. die 8 Ecken ${\tfrac {1}{2}}(1\pm {\mathrm i}\pm {\mathrm j}\pm {\mathrm k})$ und ${\tfrac {1}{2}}$ als Mittelpunkt. Die Mittelpunkte der Würfel sind $\in {\tfrac {1}{2}}{\mathsf {Q}}_{8}$ .

Der 8-Zeller ist zum 16-Zeller dual, gehört zu den 6 regulären konvexen 4-Polytopen, hat Schläfli-Symbol {4,3,3} und ist berandet von 8 Zellen (den Würfeln), 24 Quadraten, 32 Kanten und 16 Ecken. Sein 4-Volumen ist 1 bei einer Kantenlänge und einem Umkreisradius von 1.

Regulärer 24-Zeller (Ikositetrachor)

3D-Projektion des regulären 24-Zellers

Schlegeldiagramm des regulären 24-Zellers (Ecken und Kanten)

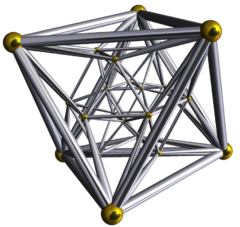
Die Elemente der Gruppe $Q_{{24}}$ haben alle die Norm 1 und bilden die Ecken des sogenannten 24-Zellers, auch Ikositetrachōr(on) (das, englisch icositetrachoron, von griechisch εἰκοσιτετράχωρον aus eikosi ‚zwanzig‘ und tetra, Präfixform von τέτταρα, ‚vier‘ und chōros ‚Raum‘), eingeschrieben in die Einheits-3-Sphäre. Die 6 Quaternionen $1,{\mathrm i},{\tfrac {1}{2}}(1+{\mathrm i}\pm {\mathrm j}\pm {\mathrm k})$ markieren die Ecken eines regulären Oktaeders mit dem Mittelpunkt ${\tfrac {1}{2}}(1+{\mathrm i})$ auf dem Rand dieses 24-Zellers, welches bei (linker wie rechter) Multiplikation mit einem Element $\in Q_{{24}}\!\setminus \!\{1\}$ in ein anderes Oktaeder (auf dem Rand) übergeht. Somit besteht der Rand des 24-Zellers aus 24 (regulären) Oktaeder-Zellen, von denen sich 6 an jeder Ecke und 3 an jeder Kante treffen. Der 24-Zeller gehört zu den 6 regulären konvexen 4-Polytopen, hat 24 Zellen (die Oktaeder), 96 Dreiecksflächen, 96 Kanten und 24 Ecken. Das 4-Volumen ist 2 bei einer Kantenlänge und einem Umkreisradius von 1.

Der 24-Zeller hat Schläfli-Symbol {3,4,3}, ist das einzige selbst-duale reguläre euklidische Polytop, das nicht Simplex oder Polygon ist, und hat insoweit keine Entsprechung in anderen Dimensionen.^{[Anm
3]}

Parkettierung und Sphärenpackung

Zu jedem der 3 oben genannten regulären 4-Polytope gibt es eine reguläre und lückenlose Parkettierung – und diese sind die einzigen – des 4-dimensionalen euklidischen Raums.

Parkettierung mit dem 8-Zeller

Eine Parkettierung des $\mathbb {R} ^{4}$ mit dem Tesserakt lässt sich so einrichten, dass die Mittelpunkte der Tesserakte, der Maschen, genau auf die Lipschitzquaternionen $\in L$ fallen. Das gelingt mit dem oben erwähnten Tesserakt, genauer: dem 4-dimensionalen und für die Disjunktheit der Maschen rechtsoffenen Intervall ${[{-{\tfrac {1}{2}},{\tfrac {1}{2}}}[}^{4}$ als der Grundmasche.

Diese Parkettierung mit dem 8-Zeller sei als die Lipschitz-Parkettierung bezeichnet. Sie hat Schläfli-Symbol {4,3,3,4} und ist zu sich selbst dual, d.h., die Mittelpunkte der einen Parkettierung sind die Ecken der dualen und umgekehrt. Das 4-Volumen der Maschen ist 1 bei einer Kantenlänge und einem Umkreisradius von 1.^{[Anm
4]}

Parkettierung mit dem 24-Zeller

Eine Parkettierung des $\mathbb {R} ^{4}$ mit dem 24-Zeller lässt sich so einrichten, dass die Mittelpunkte der 24-Zeller genau auf die Hurwitzquaternionen $\in H$ fallen. Die Grundmasche ist der 24-Zeller mit dem Mittelpunkt $0$ und den 24 Ecken der Art ${\tfrac {1}{2}}(\pm 1\pm \mathrm {i} ),\dots \,$ .^{[Anm
5]}

Diese Parkettierung mit dem 24-Zeller sei als die Hurwitz-Parkettierung bezeichnet. Ihr Schläfli-Symbol ist {3,4,3,3}. Das 4-Volumen der Maschen ist ${\tfrac {1}{2}}$ bei einer Kantenlänge und einem Umkreisradius von ${\tfrac {1}{{\sqrt {2}}}}$ .^{[Anm
6]}

Parkettierung mit dem 16-Zeller

Es gibt eine Parkettierung mit dem 16-Zeller, die dual ist zur Parkettierung mit dem 24-Zeller, – Schläfli-Symbol also {3,3,4,3}. Das 4-Volumen ihrer Maschen ist ${\tfrac {1}{6}}$ bei einer Kantenlänge von 1 und einem Umkreisradius von ${\tfrac {1}{{\sqrt {2}}}}$ .^{[Anm 7]}

Sphärenpackung

Im Zusammenhang mit diesen letzteren 2 Parkettierungen steht eine maximale (bewiesen für Gitter-Packungen, nicht aber für Nicht-Gitter-Packungen) Packungsdichte von 4-Kugeln (3-Sphären) von ${\tfrac {\pi ^{2}}{16}}\approx 0{,}6168503$ auf dem Hurwitz-Gitter F₄ im $\mathbb {R} ^{4}$ . Diese Sphärenpackung kommt auf eine Kusszahl von 24 (als obere Grenze – auch unter Nicht-Gitter-Packungen – bewiesen).^{[Anm
8]}

Maschenradius

Für die Division mit Rest weiter unten benötigen wir die Gitterweite $|G|_{{\operatorname {m}}}$ eines Gitters und definieren sie als die größte vorkommende Entfernung

$|G|_{{\operatorname {m}}}:=\operatorname {max}\,\left\{|\gamma _{G}(\xi )-\xi |\;\mid \xi \in {\mathbb {H}}\right\}$

eines Punktes $\xi \in {\mathbb {H}}$ zu einem Gitterpunkt $\gamma _{G}(\xi )\in G$ , der ihm am nächsten liegt, d.h.

$|\gamma _{G}(\xi )-\xi |=\operatorname {min}\,\{|\gamma -\xi |\;\mid \gamma \in G\}$ .^{[Anm
9]}

Das Gitter hat den Maschenradius $|L|_{{\operatorname {m}}}=1$ .^{[Anm
10]}

Pseudocode für die Approximation einer Quaternion $\xi$ durch eine Lipschitz-Ganzzahl $\gamma _{L}(\xi )$ :

$\operatorname {RundungZuLipschitz} (\xi )\;\{$	beliebige Quaternion $\xi \in {\mathbb {H}}$
${\mathrm {for}}\;i=0\;{\mathrm {to}}\;3\;\{$	alle 4 Komponenten $x_{0}+x_{1}\,{\mathrm i}+x_{2}\,{\mathrm j}+x_{3}\,{\mathrm k}:=\xi$
$g_{i}=\lfloor x_{i}+{\tfrac {1}{2}}\rfloor \;\}$	Rundung zur nächsten Ganzzahl $g_{i}\in \mathbb{Z }$ per $+{\tfrac {1}{2}}$ und Gaußklammer
${\mathrm {return}}\;\gamma \;\}$	$\gamma :=g_{0}+g_{1}\,{\mathrm i}+g_{2}\,{\mathrm j}+g_{3}\,{\mathrm k}\in L$

Damit ist $\xi$ in der Masche mit Mittelpunkt $\gamma$ , genauer: $\xi \in {[{\gamma -\varepsilon ,\gamma +\varepsilon }[}$ (rechtsoffenes 4-dimensionales Intervall).^{[Anm
11]}

Das Gitter hat den Maschenradius $|H|_{{\operatorname {m}}}={\tfrac {1}{{\sqrt {2}}}}$ .^{[Anm
12]}

Pseudocode für die Approximation einer Quaternion $\xi$ durch eine Hurwitz-Ganzzahl $\gamma _{H}(\xi )$ :

$\operatorname {RundungZuHurwitz} (\xi )\;\{$	beliebige Quaternion $\xi \in {\mathbb {H}}$
$\gamma =\operatorname {RundungZuLipschitz} (\xi )$	Lipschitz-Ganzzahl $\gamma$
$\alpha =0\;$
$s=\\|\gamma -\xi \\|\qquad$	Abweichung der Lipschitz-Näherung
$\mathrm {for} \;\beta \in Q_{24}\setminus Q_{8}\;\{\;$	Alle 16 halbzahligen Hurwitzeinheiten werden durchprobiert.
$t=\\|\gamma +\beta -\xi \\|$	Abweichung einer Hurwitz-Ganzzahl
${\mathrm {if}}\;t<s\;{\mathrm {then}}\;\{$
$\alpha =\beta$	Der Gitterpunkt mit der kleinsten Abweichung wird festgehalten.
$s=t\;\}\}$
$\gamma =\gamma +\alpha$
${\mathrm {return}}\;\gamma \;\}$	$\gamma \in H$

Die normmäßige Abweichung des Ergebnisses ist $\|\gamma -\xi \|=|\gamma -\xi |^{2}\leq |H|_{{\operatorname {m}}}^{2}={\tfrac {1}{2}}$ .^{[Anm 13]} ^{[Anm
14]}

Euklidizität

Der folgende Pseudocode ermittelt zu einer linken Division mit „kleinem“ Rest den Rest:

$\operatorname {DivisionsRest} _{L}(\alpha ,\beta )\;\{$	Dividend $\alpha \in H$ , Divisor $\beta \in H\!\setminus \!\{0\}$
$\mu =\beta ^{{-1}}\cdot \alpha$	Division links ergibt rechten Quotienten.
$\nu =\alpha -\beta \cdot \operatorname {RundungZuHurwitz} (\mu )$	Rest der linken Division
${\mathrm {return}}\;\nu \;\}$	betragsmäßig minimal

Das Suffix ${}_{L}$ kennzeichnet das Ergebnis als einer linken Division entstammend. Damit ist es in einer nachfolgenden komplementären Multiplikation zur Verwendung als linker Faktor (Teiler) geeignet.

Diese Division mit Rest macht den Ring der Hurwitzquaternionen zu einem rechts-euklidischen Ring, d.h., zu 2 Zahlen $\alpha$ und $\beta \in H\!\setminus \!\{0\}$ gibt es $\mu _{R}$ und $\nu _{R}\in H$ mit

$\alpha =\beta \cdot \mu _{R}+\nu _{R}$ und $\|\nu _{R}\|<\|\beta \|$ .^{[Anm
15]}

Wie in kommutativen euklidischen Ringen ist jedes Ideal in ein Hauptideal – nur muss zusätzlich die Seitigkeit (hier zunächst: rechts) des Ideals angegeben werden.^{[Anm
16]}

Der folgende Pseudocode zeigt einen euklidischen Algorithmus zum Auffinden eines linken größten gemeinsamen Teilers (ggT) zweier Hurwitzquaternionen in .

$\operatorname {ggT} _{L}(\alpha ,\beta )\;\{$	Hurwitzquaternionen $\alpha,\beta$
${\mathrm {while}}\;\beta \neq 0\;\{$
$\delta =\beta$
$\beta =\operatorname {DivisionsRest} _{L}(\alpha ,\delta )$	der Rest aus der Division $\delta ^{{-1}}\cdot \alpha$
$\alpha =\delta \,\}$
${\mathrm {return}}\;\alpha \;\}$

Das Ergebnis ist ein linker Teiler $\delta \in H$ von $\alpha$ und $\beta$ , d.h., es gibt $\mu ,\nu \in H$ mit $\alpha =\delta \cdot \mu$ und $\beta =\delta \cdot \nu$ . Er ist bis auf rechtsseitige Multiplikation mit einer Hurwitz-Einheit $\xi \in Q_{24}$ eindeutig bestimmt, bspw. $\delta ':=\delta \cdot \xi$ und $\mu ':=\xi ^{-1}\cdot \mu$ . Man kann also stets eine Lipschitzquaternion als Ergebnis des Algorithmus auswählen. Außerdem ist $\delta$ auch größter Teiler, d.h., es gibt kein betragsmäßig größeres $\delta '\in H$ mit $\|\delta '\|>\|\delta \|$ , das linker Teiler von $\alpha$ und $\beta$ ist. Das bedeutet auch, dass der linke ggT der beiden obigen rechtsseitigen Faktoren von $\delta$ eine Einheit ist: $\operatorname {ggT} _{L}(\mu ,\nu )=1$ .

Generell kann man die beiden Faktoren bei jeder Quaternionenmultiplikation $\cdot$ und gleichzeitig überall die Begriffe „rechts“ und „links“ vertauschen, was zu den Funktionen $\operatorname {DivisionsRest} _{R}(\alpha ,\beta )$ und $\operatorname {ggT} _{R}(\alpha ,\beta )$ führt.

Der Ring ist also auch links-euklidisch, d.h., zu 2 Zahlen $\alpha$ und $\beta \in H\!\setminus \!\{0\}$ gibt es $\mu _{L}$ und $\nu _{L}\in H$ mit

$\alpha =\mu _{L}\cdot \beta +\nu _{L}$ und $\|\nu _{L}\|<\|\beta \|$ .

Und jedes Linksideal in ist ein Links-Hauptideal.

Fazit: ist zweiseitig euklidisch – oder euklidisch schlechthin.

Einige einfache Rechenregeln für den ggT für beliebige $\alpha ,\beta \in H$ , wobei das Suffix ${}_{X}\in \{{}_{L},{}_{R}\}$ für eine der Seitigkeiten des ggT steht:

$\operatorname {ggT} _{X}(\alpha ,0)=\alpha$ und $\operatorname {ggT} _{X}(\alpha ,1)=1$
$\operatorname {ggT} _{X}(\alpha ,\beta )=\operatorname {ggT} _{X}(\beta ,\alpha )$
$\operatorname {ggT} _{L}(\xi \cdot \alpha ,\xi \cdot \beta )=\xi \cdot \operatorname {ggT} _{L}(\alpha ,\beta )$ und analog $\operatorname {ggT} _{R}(\alpha \cdot \xi ,\beta \cdot \xi )=\operatorname {ggT} _{R}(\alpha ,\beta )\cdot \xi$
$\operatorname {ggT} _{R}({\bar {\alpha }},{\bar {\beta }})={\overline {\operatorname {ggT} _{L}(\alpha ,\beta )}}$

Und es gilt auch das beidseitige Lemma von Bézout, d.h., es gibt

$\xi _{R},\eta _{R}\in H$ mit $\operatorname {ggT} _{L}(\alpha ,\beta )=\alpha \cdot \xi _{R}+\beta \cdot \eta _{R}$ (linkes Lemma von Bézout)

$\xi _{L},\eta _{L}\in H$ mit $\operatorname {ggT} _{R}(\alpha ,\beta )=\xi _{L}\cdot \alpha +\eta _{L}\cdot \beta$ (rechtes Lemma von Bézout)

wobei die $\xi _{X},\eta _{X}$ als Nebenprodukte des resp. euklidischen Algorithmus anfallen (und auch aus der Funktion $\operatorname {ggT} _{X}(\alpha ,\beta )$ herausgeführt werden können, s. den Artikel Erweiterter euklidischer Algorithmus).

Automorphismen

Als Automorphismus einer algebraischen Struktur gilt eine bijektive Abbildung $f \colon X \to X$ , bei der alle algebraischen Verknüpfungen homomorph behandelt werden, d.h. bspw.

$f(\xi \cdot \eta )=f(\xi )\cdot f(\eta )$ .

Der Primkörper $\mathbb {Q}$ des Schiefkörpers muss immer fest bleiben. Dagegen können die 3 imaginären Einheiten $\mathrm i , \mathrm j , \mathrm k$ (die die Quaternionengruppe Q₈ erzeugen) in eine jeweils andere überführt werden. Die Automorphismen von Q₈ lassen sich alle zu Automorphismen von (eindeutig) fortsetzen. Die Untergruppen und $Q_{{24}}$ von erben diese Automorphismen durch Einschränkung. Somit sind die Automorphismengruppen $\operatorname {Aut}(S)$ , $\operatorname {Aut}(H)$ und $\operatorname {Aut}(Q_{{24}})$ isomorph zu $\operatorname {Aut}({\mathsf {Q}}_{8})$ und zur Drehgruppe des Oktaeders, die wiederum zur symmetrischen Gruppe S₄ isomorph ist.

Die Automorphismen lassen sich durch (für ) „innere“ Automorphismen realisieren:

Von den 24 Quaternionen

$\lambda \in (1\!+\!{\mathrm i})\cdot Q_{{24}}$

werden auf Automorphismen vermittelt vermöge $\xi \mapsto \lambda ^{{-1}}\cdot \xi \cdot \lambda$ . Die ändern sich nicht, wenn wir die $\lambda$ auf die Einheits-3-Sphäre projizieren. Die Ergebnisse ${\tfrac {1}{{\sqrt {2}}}}\lambda$ erzeugen die Gruppe $Q_{{48}}$ , welche $=Q_{{24}}\cup {\tfrac {1}{{\sqrt {2}}}}(1\!+\!{\mathrm i})\cdot Q_{{24}}$ und isomorph zur binären Oktaedergruppe 2O ist, 48 Elemente und Zentrum $Z = \left\{\pm 1 \right\}$ hat.

Die Faktorgruppe $Q_{{48}}/Z$ hat 24 Elemente und ist damit isomorph zu den hier besprochenen Automorphismengruppen (und zur symmetrischen Gruppe S₄).

Die Konjugation als Spiegelung an der reellen Achse ist involutiv und (wie schon bei Q₈) antihomomorph in der Multiplikation, d.h.

$\overline {\xi \cdot \eta }={\bar \eta }\cdot {\bar \xi }$ ,

und wird deshalb als involutiver Antiautomorphismus bezeichnet.

Assoziierte Elemente

→ Hauptartikel: Assoziierte Elemente

Der Begriff der zueinander assoziierten Elemente kann für nicht-kommutative Ringe etwas weiter gefasst werden: 2 Elemente $\xi$ und $\eta$ sind zueinander erweitert assoziiert, wenn es 2 Einheiten $\alpha ,\beta \in Q_{{24}}$ gibt mit $\eta =\alpha \cdot \xi \cdot \beta$ . Zu einer Hurwitzquaternion gibt es höchstens 24²/2 = 288 erweitert Assoziierte, da auf einer der beiden Seiten die ganze Gruppe $Q_{{24}}$ auf der anderen nur die Faktorgruppe modulo dem Zentrum durchlaufen werden muss. Die Assoziiertheit ist wie im kommutativen Fall eine Äquivalenzrelation.

Ist $\xi \in H\!\setminus \!L$ , so ist entweder $\varepsilon \cdot \xi \in L$ oder ${\bar \varepsilon }\cdot \xi \in L$ (siehe Hurwitz-Gitter), d.h., zu jeder Hurwitzquaternion gibt es links (und genauso rechts) assoziierte Lipschitzquaternionen.

Die Konjugierte ist normalerweise nicht assoziiert.

Ideale

Die Hurwitzquaternionen bilden eine Ordnung (im Sinn der Ringtheorie) in ihrem Quotientenkörper, dem Divisionsring (Schiefkörper) der Quaternionen mit rationalen Koeffizienten. Sie sind dort sogar eine Maximalordnung oder auch Ganzheitsring. Die Lipschitzquaternionen – als auf den ersten Blick näher liegende Kandidaten für das Konzept ganzer Quaternionen – stellen auch eine Ordnung dar, sind aber nicht maximal und haben keine Division mit kleinem Rest. Deshalb sind sie weniger geeignet für die Entwicklung einer Idealtheorie, die mit der algebraischen Zahlentheorie vergleichbar wäre. Adolf Hurwitz hat dies erkannt – ein großer Schritt in der Theorie der Maximalordnungen. Ein anderer war die Feststellung, dass sie – bei einem nicht-kommutativen Ring wie – nicht eindeutig sind (alle rein imaginären Einheitsquaternionen haben zum Quadrat), so dass man sich auf eine festlegen muss, wenn man das Konzept der algebraischen ganzen Zahl auf den Schiefkörper übertragen möchte.

Für $\lambda \in H$ mit $\|\lambda \|=2$ , also $\lambda \in (1\!+\!{\mathrm i})\cdot Q_{{24}}$ , ist der Automorphismus $\xi \mapsto \lambda ^{{-1}}\cdot \xi \cdot \lambda$ von auch ein (äußerer) Automorphismus von . Das Linksideal ${\mathit {\Lambda }}=H\cdot \lambda$ ist gleich

$(\lambda \cdot \lambda ^{{-1}})\cdot H\cdot \lambda =\lambda \cdot (\lambda ^{{-1}}\cdot H\cdot \lambda )=\lambda \cdot H$ ,

somit auch Rechtsideal, also zweiseitig und gleich für alle diese 24 Erzeugenden $\lambda \;$ . Ferner ist es ein maximales Ideal mit Faktorring $H/{\mathit {\Lambda }}$ isomorph zu ${\mathbb {F}}_{{2^{2}}}=GF(2^{2})$ , dem endlichen Körper der Charakteristik 2, dessen multiplikative Gruppe isomorph ist zu $Q_{{24}}/{\mathsf {Q}}_{8}\;$ und der die 3-ten primitiven Einheitswurzeln enthält (siehe Additions- und Multiplikationstafel). ${\mathit {\Lambda }}$ ist genauso maximal in mit Faktorring $L/{\mathit {\Lambda }}\cong {\mathbb {F}}_{{2}}=GF(2)$ .^{[Anm
17]}

Prime Elemente, Faktorisierung

Eine Hurwitzquaternion ist prim in genau dann, wenn ihre Norm prim in $\mathbb {Z}$ ist.

Folgende Besonderheiten der natürlichzahligen (rein reellen) Hurwitzquaternionen sind im Kontext der Primelementzerlegung von Belang:

ist mit jeder anderen Hurwitzquaternion $\xi$ vertauschbar, d.h., $n\cdot \xi =\xi \cdot n$ .
Ein ist niemals prim in .
Ist prim in $\mathbb {Z}$ , dann gibt es nach dem Satz von Jacobi $8\,(n+1)$ prime Hurwitzquaternionen mit ganzzahligen Koeffizienten $(\xi \in L)$ und $16\,(n+1)$ Hurwitzquaternionen mit halbzahligen Koeffizienten $(\xi \in L+\varepsilon )$ , deren Norm ist (und die deshalb nur ausnahmsweise zueinander assoziiert oder konjugiert sein können).^{[Anm
18]}

Jede Hurwitzquaternion lässt sich in Primteiler zerlegen, wobei die Reihenfolge der Primteiler in folgendem Sinn vorgegeben werden kann: Sei $\xi \in H$ eine Hurwitzquaternion und

$\|\xi \|=p_{1}\;p_{2}\;\dots \;p_{n}$

eine Zerlegung ihrer Norm in Primfaktoren $\in \mathbb{N}$ . Dann gibt es zu jeder Reihenfolge dieser Primfaktoren eine Zerlegung von

$\xi =\pi _{1}\cdot \pi _{2}\cdot \ldots \cdot \pi _{n}$

in Primelemente in mit

$\|\pi _{i}\|=p_{i}$ für $i=1,2,\dots ,n$ .^{[Anm
19]}

Bei vorgegebener Primzahlsequenz ist die Faktorisierung bis auf Einheiten zwischen den Primelementen bzw. links und rechts davon und den vielen Aufspaltungsmöglichkeiten eines natürlichen Teilers (dazu muss in der Primzahlsequenz eine Primzahl mindestens 2 Mal vorkommen) eindeutig. Für die Faktorisierung in $\mathbb {Z}$ stehen mehrere Algorithmen zur Verfügung. Ein der Primzahl $p_{1}$ in $\mathbb {Z}$ korrespondierendes Primelement $\pi _{1}$ in kann man bspw. mit der oben beschriebenen Funktion $\operatorname {ggT} _{L}(\xi ,p_{1})$ dingfest machen und dann eben links von $\xi$ abspalten. Ist das Ergebnis von $\operatorname {ggT} _{L}(\xi ,p_{1})=p_{1}$ , dann kommt die Primzahl $p_{1}$ in der Primzahlsequenz mindestens 2 Mal vor, und man kann unter ihren vielen Jacobi-Aufspaltungen ein beliebiges Primelement auswählen.^{[Anm
20]}

Metrik, Vervollständigung und Potenzreihenentwicklung

Archimedische Bewertung und Metrik

Die „natürliche“ Bewertung des Schiefkörpers ist die Betragsbewertung

$|\xi |={\sqrt {\|\xi \|}}$ .

Da jede Größe durch Vervielfachung einer Einheitsgröße betragsmäßig überholt werden kann, wird diese Bewertung archimedisch genannt.^{[Anm
21]} Dieser Betrag induziert die Metrik

$\operatorname {d}_{{\infty }}(\xi ,\eta ):=|\xi -\eta |$ ,

die genau dem euklidischen Abstand im $\mathbb {R} ^{4}$ entspricht. Sie erfüllt bekanntlich die Axiome für Metriken:

(1) Definitheit	$\operatorname {d}_{{\infty }}\left(\xi ,\eta \right)=0\iff \xi =\eta$ ,
(2) Symmetrie	$\operatorname {d}_{{\infty }}\left(\xi ,\eta \right)=\operatorname {d}_{{\infty }}(\eta ,\xi )$ ,
(3) Dreiecksungleichung	$\operatorname {d} _{\infty }\left(\xi ,\eta \right)\leq \operatorname {d} _{\infty }(\xi ,\vartheta )+\operatorname {d} _{\infty }(\vartheta ,\eta )$ .

Die Vervollständigung von für die Metrik $\operatorname {d}_{{\infty }}$ führt zu $\mathbb {H}$ , den Quaternionen mit reellen Koeffizienten. Die Vervollständigung von für die Metrik $\operatorname {d}_{{\infty }}$ führt zu nichts Neuem, da eine diskrete Teilmenge von $\mathbb {H}$ ist.

Zu jeder Hurwitzquaternion $\xi \in H$ gibt es eine eindeutige Darstellung durch jede der zwei endlichen Reihen

$\xi =\sum _{i=0}^{n}\eta _{i}\cdot \varrho ^{i}$ oder $\xi =\sum _{{i=0}}^{n}\varrho ^{i}\cdot \vartheta _{i}$

mit der Basis $\varrho :={\mathrm i}\!-\!1$ , Ziffern $\eta _{i},\vartheta _{i}\in C:=\{0,1,\varepsilon ,\zeta \}$ (s. Abschnitt Hurwitz-Einheiten), Basispotenzen rechts bzw. links davon und einem $n\in \N_0$ mit $\|\varrho \|^{n}=2^{n}\geq \|\xi \|$ .

Dieses Stellenwertsystem, das sich auf ganz $\mathbb {H}$ erweitern lässt, hat folgende Eigenschaften:

Es kommt ohne „Vorzeichen“ aus.
Die Darstellung ist fast überall umkehrbar eindeutig.^{[Anm
22]}
Die Hurwitzquaternionen entsprechen genau den Darstellungen ohne Nachkommastelle.
Die Elemente $\in S$ , und nur diese rationalen Elemente, haben periodische Darstellungen.^{[Anm
23]}

Nichtarchimedische Bewertung und Metrik

Zu einer festen Primzahl sei für jedes $\xi \in S$

$\operatorname {v}_{p}(\xi ):=n$ mit $\|\xi \|={\tfrac {s}{t}}\;p^{n},p\nmid s\in \mathbb{N} ,p\nmid t\in \mathbb{N} ,n\in \mathbb{Z } \cup \{\infty \}$

der -Exponent der Norm. Diese (Exponenten-)Bewertung erfüllt:

(A) Definitheit	$\operatorname {v}_{p}(\xi )=\infty \iff \xi =0$ ,
(B) Multiplikativität	$\operatorname {v}_{p}(\xi \cdot \eta )\;=\;\operatorname {v}_{p}(\xi )+\operatorname {v}_{p}(\eta )$ ,
(C) verschärfte Dreiecksungleichung	$\operatorname {v}_{2}(\xi +\eta )\geq \min \left(\operatorname {v}_{2}(\xi ),\operatorname {v}_{2}(\eta )\right)$ .

Man beachte, dass der -Exponent der Norm zu einer Primzahl p>2 die Bedingung (C) nicht erfüllt.^{[Anm
24]} Dass es bei p=2 klappt, liegt an der Zweiseitigkeit des Ideals ${\mathit {\Lambda }}$ .

Man kann $\operatorname {v}_{p}$ eine Gruppe von „Einheiten“

$U_{p}:=\left\{\xi \in S\mid \operatorname {v}_{p}(\xi )=0\right\}$

zuordnen, zu der es für p=2 einen Bewertungsring gibt.^{[Anm
25]}

Der Bewertungsring zu $\operatorname {v}_{2}$ ist

$A:=\left\{\xi \in S\mid \operatorname {v}_{2}(\xi )\geq 0\right\}=H\cdot U_{2}=HN$ ,

ein lokaler Ring mit dem maximalen Ideal

${\mathfrak m}:=\left\{\xi \in S\mid \operatorname {v}_{2}(\xi )>0\right\}={\mathit {\Lambda }}\cdot U_{2}={\mathit {\Lambda }}N$ ,

wobei $N:=\{{\tfrac {1}{t}}\;\mid \;2\nmid t\in \mathbb{N} \}$ die (skalaren) Normen der Nenner von $U_{2}$ beisteuert. Den Anschluss zu den 2-adisch ganzrationalen Zahlen schafft wegen $\mathbb{Z } _{{(2)}}=\mathbb{Z } \,N$ die Gleichung

$A=\left\{\xi =x_{0}+x_{1}\,\mathrm {i} +x_{2}\,\mathrm {j} +x_{3}\,\mathrm {k} \;\mid \;(x_{0},x_{1},x_{2},x_{3})\in {\mathbb {Z} _{(2)}}^{4}\,\cup \,({\tfrac {1}{2}}+\mathbb {Z} _{(2)})^{4}\right\}$ .^{[Anm
26]}

Die durch $\operatorname {v}_{2}$ definierte Abstandsfunktion

$\operatorname {d}_{2}(\xi ,\eta ):=2^{{-\operatorname {v}_{2}(\xi -\eta )}}$

erfüllt ebenfalls die Axiome für Metriken. Dazu noch die

verschärfte Dreiecksungleichung $\operatorname {d}_{2}\left(\xi ,\eta \right)\leq \max \left(\operatorname {d}_{2}(\xi ,\zeta ),\operatorname {d}_{2}(\zeta ,\eta )\right)$ ,

die $\operatorname {d}_{2}$ zu einer Ultrametrik macht. Die Vervollständigung von für diese Metrik führt zu

${\hat S}:=\left\{\xi =x_{0}+x_{1}\,{\mathrm i}+x_{2}\,{\mathrm j}+x_{3}\,{\mathrm k}\;\mid \;x_{0},x_{1},x_{2},x_{3}\in \mathbb{Q} _{2}\right\}$ ,

den Quaternionen mit 2-adischen Koeffizienten. Der vervollständigte Bewertungsring ist

${\hat A}:=\{\xi \in {\hat S}\mid \operatorname {{\hat v}_{2}}(\xi )\geq 0\}$ ,

der mit der Vervollständigung ${\hat {H}}$ des Rings der Hurwitzquaternionen zusammenfällt, weil in $\operatorname {d}_{2}$ -dicht liegt^{[Anm
27]}. Hierbei ist $\operatorname {{\hat v}_{2}}$ die eindeutige Fortsetzung von $\operatorname {v_{2}}$ auf ${\hat S}$ .

Aus den Nebenklassen
des Ideals ${\mathit {{\hat \Lambda }}}$ zu bildende
Ringe ${\hat L}$ und ${\hat {H}}$
		$\widehat {[0]}\cup \widehat {[1]}\cup \widehat {[\varepsilon ^{4}]}\cup \widehat {[\varepsilon ^{2}]}$ $={\hat L}\cup \widehat {\varepsilon ^{4}\!+\!L}={\hat H}$
		$\mid$
		$\widehat {[0]}\cup \widehat {[1]}$ $={\hat L}$
		$\mid$
		$\widehat {[0]}$ $={\mathit {{\hat \Lambda }}}$

Das vervollständigte Bewertungsideal ist

${\hat {{\mathfrak m}}}:={\mathit {{\hat \Lambda }}}:=\{\xi \in {\hat S}\mid \operatorname {{\hat v}_{2}}(\xi )>0\}={\hat H}\cdot \lambda =\lambda \cdot {\hat H}$ ,

wo $\lambda \in {\hat H}$ mit $\operatorname {{\hat v}_{2}}(\lambda )=1$ , und der Restklassenkörper ${\hat H}/{\mathit {{\hat \Lambda }}}$ ist isomorph zu dem im Abschnitt Ideale erwähnten $H/{\mathit {\Lambda }}\cong {\mathbb {F}}_{{2^{2}}}$ .

Wenn wir ${\hat {{\color {White}\_}}}$ als Vervollständigungsoperator nehmen, erhalten wir das nebenstehende Diagramm für die Vervollständigungen der Nebenklassen von ${\mathit {\Lambda }}$ , die allerdings im Unterschied zu oben keine Gitter mehr sind.

Wie bei den p-adischen Zahlen haben wir, bei einem festen Primelement $\lambda \in (1\!+\!{\mathrm i})\cdot Q_{{24}}$ , eine eindeutige $\lambda$ -adische Darstellbarkeit eines Elementes $\xi \in {\hat S}$ durch jede der zwei $\operatorname {d}_{2}$ -konvergenten Reihen

$\xi =\sum _{i=\operatorname {v} _{2}(\xi )}^{\infty }\lambda ^{i}\cdot \zeta _{i}$ oder $\xi =\sum _{{i=\operatorname {v}_{2}(\xi )}}^{\infty }\vartheta _{i}\cdot \lambda ^{i}$

mit $\zeta _{i},\vartheta _{i}\in Q_{4}$ (s.o. Repräsentantensystem) und Potenzen der Basis links bzw. rechts davon. Die Elemente $\in S$ , und nur diese rationalen Elemente, haben periodische Darstellungen.^{[Anm
28]} ^{[Anm
29]}

Siehe auch

Die 5 Platonischen Körper im $\mathbb {R} ^{3}$

Literatur

John Horton Conway, Derek Alan Smith: On quaternions and octonions: their geometry, arithmetic, and symmetry. A K Peters Ltd., 2003, ISBN 978-1-56881-134-5.

Harold Scott MacDonald Coxeter: Regular Polytopes, 3rd ed. Dover Publications, 1973, ISBN 0-486-61480-8.

Godfrey Harold Hardy, E. M. Wright: Einführung in die Zahlentheorie, Kap. 20. R. Oldenbourg, München 1958.

Anmerkungen

↑ Denn ist $\xi \in L$ , dann ist entweder $\xi \in {\mathit {\Lambda }}$ oder $\xi -1\in {\mathit {\Lambda }}$ ; ist jedoch $\xi \in H\!\setminus \!L$ , dann ist $\xi -\varepsilon ^{4}\in L$ und entweder $\xi -\varepsilon ^{4}\in {\mathit {\Lambda }}$ oder $\xi -\varepsilon ^{4}-1=\xi +\varepsilon ^{2}\in {\mathit {\Lambda }}$ , welch letzteres $\Leftrightarrow \xi -\varepsilon ^{2}\in {\mathit {\Lambda }}$ .     Somit gibt es zu beliebigen $\xi ,\eta \in H$ Repräsentanten $\zeta _{{\xi }},\zeta _{{\eta }}\in Q_{4}$ und Elemente $\lambda _{{\xi }},\lambda _{{\eta }}\in {\mathit {\Lambda }}$ derart, dass $\xi =\zeta _{{\xi }}+\lambda _{{\xi }}$ und $\eta =\zeta _{{\eta }}+\lambda _{{\eta }}$ . Dann ist

$\xi \cdot \eta =(\zeta _{{\xi }}+\lambda _{{\xi }})\cdot (\zeta _{{\eta }}+\lambda _{{\eta }})$

           $=\zeta _{{\xi }}\cdot \zeta _{{\eta }}+\zeta _{{\xi }}\cdot \lambda _{{\eta }}+\lambda _{{\xi }}\cdot \zeta _{{\eta }}+\lambda _{{\xi }}\cdot \lambda _{{\eta }}$

           $\in \zeta _{{\xi }}\cdot \zeta _{{\eta }}+{\mathit {\Lambda }}$ .
Wegen der multiplikativen Abgeschlossenheit von $Q_{4}$ ist auch $\zeta :=\zeta _{{\xi }}\cdot \zeta _{{\eta }}\in Q_{4}$ . Somit ist $\zeta +{\mathit {\Lambda }}=[\zeta ]$ eine der 4 Partitionen von , und es folgt das gesuchte Resultat:

$\xi \cdot \eta \in H$ .
↑ Als das $\theta \colon Q_{3}\to \operatorname {Aut} ({\mathsf {Q}}_{8})$ aus Semidirektes Produkt#Definition ist die Konjugation $\theta (q_{3})(q_{8}):=q_{3}\cdot q_{8}\cdot q_{3}^{-1}$ zu nehmen.
Neben den genannten Normalteilern Q₈ und hat $Q_{{24}}$ nur zyklische Untergruppen der Ordnungen 3, 4 und 6. Die 8 Hurwitzeinheiten ${\tfrac {1}{2}}(1\pm {\mathrm i}\pm {\mathrm j}\pm {\mathrm k})$ haben die Ordnung 6 und die 8 mit multiplizierten ${\tfrac {1}{2}}(-1\pm {\mathrm i}\pm {\mathrm j}\pm {\mathrm k})$ die Ordnung 3. Somit enthält $Q_{{24}}$ (und damit auch und ) neben 6 primitiven 4-ten auch 8 primitive 6-te aber keine primitiven 12-ten Einheitswurzeln.
↑ Im $\mathbb {R} ^{3}$ gibt es 5 reguläre Körper, die sog. Platonischen Körper. Sie haben alle eine Entsprechung im $\mathbb {R} ^{4}$ : Obiger 16-Zeller ist bspw. als Kreuz-4-Polytop das Analogon des Kreuzpolytops Oktaeder und der 8-Zeller als Maß-4-Polytop das des Maßpolytops Würfel. Und nach Coxeter, Table I: Regular polytopes, (iii) The three regular polytopes in n dimensions (n ≥ 5) Seite 294f gibt es in den Dimensionen > 4 als reguläre Polytope nur Simplex, Kreuzpolytop und Maßpolytop.
Der 24-Zeller ist zusammengesetzt aus Kreuzpolychor (16-Zeller) und Maßpolychor (8-Zeller). In jeder Dimension lässt sich Kreuzpolytop und Maßpolytop zusammensetzen, d.h. die Menge der Ecken beider Polytope auf der Einheitssphäre platzieren. Nur in der zweiten, wo es banal ist, und eben in der vierten Dimension lässt sich ein reguläres Ergebnis arrangieren.
↑ Zu jeder Dimension gibt es eine Parkettierung des euklidischen Raums mit dem Maßpolytop. Bei Dimensionen > 4 gibt es keine andere reguläre.
↑ Diese Ecken sind $\in {\tfrac {1}{2}}(1\!+\!{\mathrm i})\cdot Q_{{24}}$ , sind die Mittelpunkte der Oktaeder auf dem Rand des von der Einheitengruppe $Q_{{24}}$ markierten 24-Zellers und markieren damit den zu ihm dualen 24-Zeller. Das Oktaeder auf seinem Rand mit der Eckenkonfiguration ${\tfrac {1}{2}}\left(1+\left\{\pm {\mathrm i},\pm {\mathrm j},\pm {\mathrm k}\right\}\right)$ fällt zusammen mit dem Oktaeder mit der Eckenkonfiguration ${\tfrac {1}{2}}\left(-1+\left\{\pm {\mathrm i},\pm {\mathrm j},\pm {\mathrm k}\right\}\right)$ auf dem Rand des um versetzten 24-Zellers mit Mittelpunkt . Da aber das erstere Oktaeder durch die Multiplikation mit einem Element $\in Q_{{24}}$ in jedes der 24 Oktaeder auf dem Rand der Grundmasche überführt werden kann und dabei in jeden der 24 Gitternachbarn des Ursprungs übergeht, ferner die Elemente $\in Q_{{24}}$ – als Obermenge von $\left\{\varepsilon ,{\mathrm i},{\mathrm j},{\mathrm k}\right\}$ – das ganze Gitter erzeugen, müssen die Mittelpunkte aller Maschen dieser Parkettierung genau aus den Punkten aus bestehen.
↑ Eine Zelle (d.i. ein Oktaeder) gehört 2 Maschen an. An einer Ecke stoßen 8 Maschen zusammen; jeweils 2 Mittelpunkte solcher Maschen sind in derselben Nebenklasse von ${\mathit {\Lambda }}$ , nämlich antipodische. Es gibt keine Nachbarmasche mit nur Kante oder nur Dreieck gemeinsam. Die Maschen sind alle parallel zueinander.
↑ Es kommen also drei 16-Zeller auf einen 24-Zeller der dualen Parkettierung, genauer: 24 facettenartig um die $0$ als Pol angeordnete und an dem Oktaeder in ihrer Äquator-Hyperebene halbierte 16-Zeller füllen exakt den 24-Zeller $Q_{{24}}$ . Die Maschen fallen in 3 Parallelitätsklassen entsprechend der Gruppe $Q_{24}/{\mathsf {Q}}_{8}\cong Q_{3}$ .
↑ Dieses Phänomen hat Ähnlichkeit mit der Packung des Kreises in der Parkettierung der Ebene mit dem regulären 6-Eck bei einer Kusszahl von 6 und einer Packungsdichte von ${\tfrac {\pi }{2{\sqrt {3}}}}\approx 0{,}9068996$ . Im $\mathbb {R} ^{2}$ gibt es die Einheits-1-Sphäre, die auch eine Lie-Gruppe ist, nämlich die U(1). Das entsprechende Gitter sind die Eisenstein-Zahlen.
↑ Für die Bestimmung von $|G|_{{\operatorname {m}}}$ ist es unerheblich, welcher von den qualifizierenden Gitterpunkten $\gamma _{G}(\xi )$ ausgewählt wird, und für $\gamma _{G}(\xi )$ ist es unerheblich, ob zum Vergleichen der Betrag $|\cdot |$ oder die Norm $\|\cdot \|$ herangezogen wird. Bei einem kompakten Polytop werden die Entfernungsextrema in den Ecken angenommen. Bei ausreichender Symmetrie der Masche sind Punkte auf dem Rand von den Mittelpunkten der Maschen, auf deren Rand sie liegen, gleich weit entfernt; innere Punkte einer Masche haben einen eindeutigen nächsten Gitterpunkt, den Mittelpunkt der Masche.
↑ Die Grundmasche der Lipschitz-Parkettierung hat einen Radius von 1. Tatsächlich ergibt eine Umschau unter den 8 Gitterpunkten $\pm 1,\pm {\mathrm i},\pm {\mathrm j},\pm {\mathrm k}$ in der Nachbarschaft, dass die 16 Ecken ${\tfrac {1}{2}}(\pm 1\pm {\mathrm i}\pm {\mathrm j}\pm {\mathrm k})$ der Grundmasche (als Endpunkte der Raumdiagonalen in allen Tesserakten) von ihnen mindestens 1 entfernt sind.
↑ Diese Zuordnung eines Punktes $\xi$ zu einer Masche ist eindeutig, und die Ecke $\gamma -\varepsilon$ ist der einzige Punkt der Masche, der von $\gamma$ einen Abstand 1 hat; alle anderen sind näher.
↑ Die Grundmasche der Hurwitz-Parkettierung hat einen Radius von ${\tfrac {1}{{\sqrt {2}}}}$ . Ihre 24 Ecken von der Art

${\tfrac {1}{2}}(\pm 1\pm \mathrm {i} ),\dots \in {\tfrac {1}{2}}(1\!+\!\mathrm {i} )\cdot Q_{24}$
sind von jedem Gitterpunkt $\in H$ mindestens ${\tfrac {1}{{\sqrt {2}}}}$ entfernt.
↑ Das Ergebnis ist von vornherein eindeutig für Quaternionen, die im Inneren einer Masche der Hurwitz-Parkettierung liegen. Bei Quaternionen auf dem Rand (sie liegen ebenfalls auf dem Rand einer Nachbarmasche) bevorzugt der Pseudocode Maschenmittelpunkte $\in L$ , wodurch die Maschen inkongruent werden. Dem lässt sich abhelfen, indem man im Fall gleicher Abweichung nach lexikographischer Ordnung auswählt.
↑ Der Maschenradius des Gitters

$\mathbb {Z}$ im $\mathbb {R} ^{1}$     beträgt     $|\mathbb{Z } |_{{\operatorname {m}}}={\tfrac {1}{2}}\;$ bei einem 1-Volumen von 1,
der des Gitters der Gaußschen Zahlen

$\mathbb {Z} [\mathrm {i} _{\mathbb {C} }]$ im $\mathbb {R} ^{2}$     ist     $|\mathbb{Z } [{\sqrt[ {4}]{1}}\,]|_{{\operatorname {m}}}={\tfrac {1}{{\sqrt {2}}}}$ bei einem 2-Volumen von 1
und der des Gitters der Eisenstein-Zahlen

$\mathbb{Z } [{\tfrac {{\sqrt {-3}}}{2}}]$ im $\mathbb {R} ^{2}$     ist     $|\mathbb{Z } [{\sqrt[ {6}]{1}}\,]|_{{\operatorname {m}}}={\tfrac {1}{{\sqrt {3}}}}$ bei einem 2-Volumen von ${\tfrac {\sqrt {3}}{2}}$ .
↑ Nach dem unter Maschenradius Gesagten gilt wegen $\nu _{R}=\alpha -\beta \cdot \mu _{R}=\beta \cdot (\beta ^{-1}\cdot \alpha -\mu _{R})$ und $\|\beta ^{-1}\cdot \alpha -\mu _{R}\|\leq {\tfrac {1}{2}}$ sogar

$\|\nu _{R}\|\leq {\tfrac {1}{2}}\|\beta \|$ ,
während der Ring bei Quotienten, die genau auf die Punkte ${\tfrac {1}{2}}(\pm 1\pm {\mathrm i}\pm {\mathrm j}\pm {\mathrm k})$ fallen, die euklidische Bedingung verfehlt. Tatsächlich ist ${\mathit {\Lambda }}$ kein Hauptideal in , denn das (rechte oder linke) Erzeugnis in eines jeden der 3 Primelemente $1\!+\!{\mathrm i}$ , $1\!+\!{\mathrm j}$ oder $1\!+\!{\mathrm k}$ enthält die beiden anderen Primelemente nicht, wogegen sie in miteinander assoziiert sind und ein jedes für sich allein das Ideal ${\mathit {\Lambda }}$ erzeugt.
↑ Ist $I=\{0\}$ , dann ist ein Hauptideal. Ist $I\neq \{0\}$ ein Rechtsideal in , dann gibt es ein $\beta \in I$ mit kleinster positiver Norm. Zu jedem $\alpha \in I$ gibt es wegen der Rechts-Euklidizität $\mu _{R}$ und $\nu _{R}\in H$ mit $\alpha =\beta \cdot \mu _{R}+\nu _{R}$ und $\|\nu _{R}\|<\|\beta \|$ . Da aber $\beta$ minimal ist mit $\|\beta \|>0$ , muss $\nu _{R}=0$ sein. D.h., $\alpha =\beta \cdot \mu _{R}$ ist ein Rechts-Vielfaches von $\beta$ und das Rechts-Hauptideal $\beta \cdot H$ .
↑ Reell erzeugte Hauptideale sind ebenfalls zweiseitig, während die übrigen Nichteinheiten

$\alpha \;\in \;H\setminus \,(\mathbb{Q} \;\cup \;Q_{{24}}\;\cup \;(1\!+\!{\mathrm i})\cdot Q_{{24}})\;$
(sie haben alle eine Norm $\|\alpha \|>2\;$ ) nur einseitige Linksideale $H\cdot \alpha \;$ bzw. Rechtsideale $\alpha \cdot H$ erzeugen. Demnach ist ${\mathit {\Lambda }}$ das einzige maximale Ideal von , welches zweiseitig ist. Dennoch ist der Ring kein lokaler, da er weitere maximale (eben einseitige) Ideale enthält. Modulo einem nur einseitigen Ideal kann man einen Faktorring nicht bilden, da die zu „erbende“ Multiplikation nicht wohldefiniert werden kann (das Ideal müsste dafür Normalteiler sein und nicht nur Untergruppe). Und der Faktorring modulo einem reell erzeugten Hauptideal $\neq H$ hat Nullteiler (die Erzeugende ist nicht prim).
↑ Allgemeiner ist die Anzahl der Quadratsummenzerlegungen einer ungeraden Zahl $u>2$ als $u=a_{0}^{2}+a_{1}^{2}+a_{2}^{2}+a_{3}^{2}$ gleich $8\sigma (u)$ für $a_{i}\in \mathbb {Z}$ und gleich $16\sigma (u)$ für $a_{i}\in \mathbb {Z} +{\tfrac {1}{2}}$ mit $\sigma$ als der Teilbarkeit.
↑ Beispiel für Varianten der Primfaktorzerlegung:
(Die Vektornotation soll u.a. die Beliebigkeit der Zuordnung der Komponenten zu den Einheitsvektoren zum Ausdruck bringen.) Die zu zerlegende Hurwitzquaternion sei (13,13,13, 0) mit einer Norm von 507 = 3·13·13. Die Primzahl 13 wurde gewählt, weil sie die kleinste Primzahl ist, die 2 wesentlich verschiedene, d.h. nicht assoziierte und nicht konjugierte, Zerlegungen
- (3, 2, 0, 0)·(3,-2, 0, 0) = (2, 2, 2, 1)·(2,-2,-2,-1)
jeweils zur Primzahlsequenz 13·13 besitzt. Zur Primzahlsequenz 3·13·13 hat (13,13,13, 0) die Zerlegungen:
- ( 1, 1, 1, 0)·( 3,-2, 0, 0)·( 3, 2, 0, 0)
- ( 1, 1, 1, 0)·( 2,-2,-2,-1)·( 2, 2, 2, 1)
zur Primzahlsequenz 13·3·13
- ( 3, 2, 0, 0)·( 0, 1, 1,-1)·( 2,-2,-2, 1)
- ( 2,-2,-2,-1)·( 0, 1, 1, 1)·( 3, 2, 0, 0)
- ( 2, 2, 2, 1)·( 1,-1,-1, 0)·( 2, 2, 2,-1)
zur Primzahlsequenz 13·13·3
- ( 3, 2, 0, 0)·( 3,-2, 0, 0)·( 1, 1, 1, 0)
- ( 2, 2, 2, 1)·( 2,-2,-2,-1)·( 1, 1, 1, 0)
Es gibt unter den Zerlegungen zur Sequenz 13·3·13 übrigens keine Zerlegung des Typs (3,2,0,0)·(1,1,1,0)·(3,2,0,0).
↑ Bei den Gaußschen Zahlen $\mathbb {Z} [\mathrm {i} _{\mathbb {C} }]$ gibt es rein reelle Primelemente, nämlich die Primzahlen $p\in \mathbb{Z }$ mit $p\equiv 3{\mbox{ mod }}4$ . Die Primzahlen $p\equiv 1{\mbox{ mod }}4$ haben genau 2 Primteiler in $\mathbb {Z} [\mathrm {i} _{\mathbb {C} }]$ , die $p=(a+b\,\mathrm {i} _{\mathbb {C} })\,(a-b\,\mathrm {i} _{\mathbb {C} })$ eindeutig zerlegen und zueinander konjugiert sind.
↑ Man kann ihr eine Gruppe von „Einheiten“

$U_{{\infty }}:=\left\{\xi \in S\mid \|\xi \|=1\right\}$
zuordnen, zu der es allerdings wegen der Archimedizität keinen (Bewertungs-)Ring gibt.
↑ Alle Quaternionen mit mehrfacher Darstellung sind rational aus . Z.B. haben wir drei Darstellungen bei
$\eta :=(1+3\,{\mathrm i})/5\;=\;0{_{{_{\blacktriangleright }}}}\!\overline {010}\;=\;11{_{{_{\blacktriangleright }}}}\!\overline {001}\;=\;1110{_{{_{\blacktriangleright }}}}\!\overline {100}$
und genauso alle $\eta +\xi$ mit $\xi \in H$ , wobei die Periode wie üblich durch eine über die periodischen Ziffern gezogene Linie gekennzeichnet ist.

↑ Mit dem folgenden Pseudocode lassen sich Hurwitzquaternionen in ein Stellenwertsystem zu einer Basis $\varrho \in (1\!+\!{\mathrm i})\cdot Q_{{24}}$ mit 4 Ziffern – alle mit Norm ≤1 – codieren. Nach S. Khmelnik, der die Basis −1±i zum ersten Mal (1964) für die komplexen Zahlen vorgeschlagen hat, hängt die Endlichkeit der Darstellung sowohl von der Basis wie vom Ziffernsatz ab. Für geeignete Stellenwertsysteme sind ${\big \langle }\rho :=\mathrm {i} \!-\!1;\{0,1,\varepsilon ,\zeta \}{\big \rangle }$ mit Erzeugenden $\varepsilon ,\zeta$ von $Q_{{24}}$ (s. Abschnitt Hurwitz-Einheiten). Statt $\mathrm {i}$ kann auch jedes andere Element der Ordnung 4 $\in {\mathsf {Q}}_{8}$ genommen werden.

$\operatorname {EncodeArchim} _{R}(\xi )\;\{$	Hurwitzquaternion $\xi \in H$
" "	die leere Zeichenkette
${\mathrm {while}}\;(\xi \neq 0)\;\{\;$	Die Schleife terminiert für $\xi \in H$ und geeignete Stellenwertsysteme.
${\mathrm {for}}\;k=0\;{\mathrm {to}}\;3\;\{\;$	Genau eine der Ziffern aus dem 4-wertigen Ziffernsatz …
$\eta =\xi -C[k]$	… qualifiziert sich.
${\mathrm {if}}\;{\mathrm {mod}}(\\|\eta \\|,2)=0\;{\mathrm {then}}\;\{\;$	Wenn die Norm gerade ist, …
$\xi =\eta \cdot \varrho ^{{-1}}$	… ist diese Division (eine rechte) ohne Rest.
„ $01\varepsilon \zeta$ “	Der Code für die neue Ziffer …
	… wird dem Ergebnis links vorangestellt.
${\mathrm {break}}\;\}\}\}$
${\mathrm {return}}\;D\;\}$

Eine Überdeckung der Gaußschen Zahlen durch ein Stellenwertsystem zur Basis i-1 mit Ziffernsatz {0,1}

Das Auswahlkriterium für die Ziffern ist eines der Teilbarkeit – also ein nichtarchimedisches. Deshalb werden auch die Ziffern aufsteigend von den niedrigen zu den hohen Potenzen von $\varrho$ geliefert. Die Potenzen sind hier rechte – daher der Funktionsname – Faktoren der Ziffern. Dazu passt das von links nach rechts absteigende Horner-Schema, z. B. $(\zeta \!\cdot \!\varrho +\varepsilon )\!\cdot \!\varrho +1\;=\;\zeta \!\cdot \!\varrho ^{2}+\varepsilon \!\cdot \!\varrho ^{1}+1\!\cdot \!\varrho ^{0}\;=\;\zeta \varepsilon 1{_{{_{\blacktriangleright }}}}\!{_{{_{\varrho }}}}$ .
Üblicherweise sind bei archimedischen Stellenwertsystemen die Terme mit Exponenten ≥ 0 links; Nachkommastellen schließen sich rechts vom optionalen Stellenwert-Trennzeichen » ${\color {White}l}\!\!{_{{_{\blacktriangleright }}}}$ « an, das in seiner Asymmetrie anzeigt, in welcher Richtung die Exponenten unendlich werden können, also den Unterschied zwischen und archimedischer und nichtarchimedischer Darstellung kennzeichnet. (Bei endlichen Darstellungen spielt diese Richtung keine Rolle.) Das angehängte Subskript ${\color {White}l}\!\!{_{{_{\varrho }}}}$ drückt aus, dass $\varrho$ die Basis ist und dass deren Potenzen sich rechts von den Koeffizienten (Ziffern) befinden. Somit haben wir z.B. $\zeta \varepsilon 1{_{{_{\blacktriangleright }}}}\!{_{{_{\varrho }}}}\;=\;1\zeta 1\zeta 1\!\!\;{_{{_{\varrho }}}}\!\!\;{_{{_{\blacktriangleright }}}}\;=\;1+\varrho \!\!\;\cdot \!(\zeta +\varrho \!\cdot \!(1+\varrho \!\cdot \!(\zeta +\varrho \!\cdot \!1)))$ . Ein genuin archimedisches Auswahlkriterium für die Ziffern, welches die Ziffern von den hohen Potenzen absteigend liefert und sich für ganz $\mathbb {H}$ eignet, ist wesentlich komplizierter zu formulieren, wie man schon an der Form des nebenstehenden drachenförmigen Gebiets erkennen kann.
Es zeigt das von einer Potenz $\varrho ^{n}$ in der Gauß-Ebene in eindeutiger Weise durch Summen niedrigerer Potenzen erreichbare Gebiet in gleichen Grautönen – bei jedem Potenzschritt wird ein exaktes Duplikat der Vereinigung des Bisherigen hinzugefügt.

Additionstafel
	${\color {White}..}0{\color {White}..}$		$\varepsilon$	$\zeta$
$0$	${\color {OliveGreen}0}$	${\color {Red}1}$	${\color {OliveGreen}\varepsilon }$	${\color {Red}\zeta }$
	${\color {Red}1}$	${\color {OliveGreen}1100}$	${\color {Red}\varepsilon \varepsilon 0\zeta }$	${\color {OliveGreen}\zeta \zeta 0\varepsilon }$
$\varepsilon$	${\color {OliveGreen}\varepsilon }$	${\color {Red}\varepsilon \varepsilon 0\zeta }$	${\color {OliveGreen}\varepsilon \varepsilon 00}$	${\color {Red}1}$
$\zeta$	${\color {Red}\zeta }$	${\color {OliveGreen}\zeta \zeta 0\varepsilon }$	${\color {Red}1}$	${\color {OliveGreen}\zeta \zeta 00}$

Das additive Erzeugendensystem $\left\{\varepsilon ,{\mathrm i},{\mathrm j},{\mathrm k}\right\}$ von hat die resp. Codierungen $\left\{\;\;\;\;\varepsilon ,\;\;\;11,\;\;\zeta \zeta 1,\zeta \zeta 1\varepsilon 1\right\}$ . (Die Codierungen sind vom Typ ${\color {White}l}\!\!{_{{_{\blacktriangleright }}}}\!{_{{_{\varrho }}}}$ , die Potenzen der Basis sind also rechts. Das Trennzeichen ist bei ganzen Zahlen weggelassen.) Hiermit und mit Hilfe der gezeigten Additionstafel lässt sich jede Hurwitzquaternion codieren. (Für den Bau einer Arithmetik für die Hurwitzquaternionen sind jedoch Additionstafeln geschickter, die zu jeder der 9 Ziffernsummen zweier Summanden und jedem der 225 möglichen Überträge die neuen Überträge enthalten.) Wegen $\varepsilon \cdot \zeta =\zeta \cdot \varepsilon =1$ bedürfen von der Multiplikationstafel nur die Quadrate

$\varepsilon ^{2}\;=\;\zeta \zeta \zeta 0\zeta$ und

$\zeta ^{2}\;=\;\varepsilon \varepsilon \varepsilon 0\varepsilon$

einer Erwähnung.

Vertauschungsregeln
$\varrho ^{1}\cdot \varepsilon$	$\varepsilon \varepsilon \varepsilon \zeta 0$	$\varrho ^{1}\cdot \zeta$	$\varepsilon \varepsilon \varepsilon 0$
$\varrho ^{2}\cdot \varepsilon$	$\zeta \zeta 1\varepsilon 00$	$\varrho ^{2}\cdot \zeta$	$\varepsilon \varepsilon \varepsilon \zeta 1\zeta 00$
$\varrho ^{3}\cdot \varepsilon$	$\zeta \zeta 000$	$\varrho ^{3}\cdot \zeta$	$\zeta \zeta \zeta 0\zeta \varepsilon 000$

Mit den Vertauschungsregeln können Ziffern von der rechten auf die linke Seite von $\varrho$ gebracht werden. Da $\varrho ^{{0}}=1$ und $\varrho ^{{4}}=-4$ im Zentrum liegen, haben wir $\varrho ^{{n+4}}\cdot \varepsilon \;=\;\varrho ^{{n}}\cdot \varepsilon \cdot \varrho ^{{4}}$ und $\varrho ^{{n+4}}\cdot \zeta \;=\;\varrho ^{{n}}\cdot \zeta \cdot \varrho ^{{4}}$ , so dass sich die Tabelle auf 3 Einträge beschränken kann. Weitere Codierungsbeispiele:

$-1=\varrho ^{4}+\varrho ^{3}+\varrho ^{2}+1\;=\;11101$	$\in H$ ,
$-{\tfrac {1}{5}}=\sum _{i=1}^{\infty }\varrho ^{-4i}\;=\;{_{_{\blacktriangleright }}}\!{\overline {0001}}\;=\;0,00010001\dots$	$\in S\!\setminus \!H$ .

↑ Denn für alle Primelemente $\pi \in H$ mit $\|\pi \|=p$ ist $\operatorname {v}_{p}(\pi )=\operatorname {v}_{p}({\bar \pi })=1$ . Wenn nun der Realteil $\operatorname {Re} \pi =0$ sein sollte, dann lässt sich unter Beibehaltung des bisher Gesagten durch Multiplikation mit einer der Quaternionen $\mathrm i,\mathrm j,\mathrm k$ sicherstellen, dass $\operatorname {Re} \pi \neq 0$ . Dann ist $0<\|\operatorname {Re} \pi \|$ $=\|{\tfrac {1}{2}}(\pi +{\bar \pi })\|<p$ , also $\operatorname {v}_{p}({\mathrm {Re}}\,\pi )=0$ . Wo doch für eine Bewertung $\operatorname {v}_{p}({\mathrm {Re}}\,\pi )$ $=\operatorname {v}_{p}(\pi +{\bar \pi })$ $\geq \min \left(\operatorname {v}_{p}(\pi ),\operatorname {v}_{p}({\bar \pi })\right)=1$ sein müsste.
↑ Wir haben die Reihe von Normalteilern $Q_{{24}}\triangleleft U_{{\infty }}\triangleleft U_{p}$ . Die sind verschieden, denn es ist z.B. ${\tfrac 15}(4+2\,{\mathrm i}+2\,{\mathrm j}+{\mathrm k})\;\in \;U_{{\infty }}\!\setminus \!Q_{{24}}$ und $4+2\,{\mathrm i}+2\,{\mathrm j}+{\mathrm k}\;\in \;U_{2}\!\setminus \!U_{{\infty }}$ .
↑ ist Unterring des Schiefkörpers und ist die Lokalisierung des Rings an seinem Primideal ${\mathit {\Lambda }}$ , seiner einzigen endlichen Stelle. Die einzige unendliche Stelle ist die oben erwähnte archimedische. Die Betragsfunktion zu einer nicht-trivialen Division mit Rest ist notwendigerweise archimedisch.
↑ Wegen (Satz von Euler und eulersche φ-Funktion) ${\tfrac {1}{t}}={\tfrac {1-2^{\varphi (t)}}{t}}\,(1+2^{\varphi (t)}+2^{2\,\varphi (t)}+\dots )$ für $2\nmid t\in \mathbb{N}$

↑ In diesem Artikel seien bei nichtarchimedischen Stellenwertsystemen die Terme mit Exponenten ≥ 0 ebenfalls links vom Trennzeichen platziert; Terme mit negativen Exponenten (bei „gebrochenen“ Zahlen) sind dann rechts vom optionalen Stellenwert-Trennzeichen » ${\color {White}l}\!\!{_{{_{\blacktriangleleft }}}}$ «, das in seiner Asymmetrie anzeigt, in welcher Richtung die Exponenten unendlich werden können, also den Unterschied zwischen archimedischer und nichtarchimedischer Darstellung markiert. Das angehängte Subskript ${\color {White}l}\!\!{_{{_{\lambda }}}}$ drückt aus, dass $\lambda$ die Basis ist und dass deren Potenzen sich rechts von den Koeffizienten (Ziffern) befinden.
Z.B. ist

$-1=\lambda ^{4}+\lambda ^{3}+\lambda ^{2}+1\;=\;11101{_{{_{\blacktriangleleft }}}}{_{{_{\lambda }}}}$	im System ${\big \langle }\lambda ={\mathrm i}\!-\!1;\{0,1,\varepsilon ,{\bar \varepsilon }\}{\big \rangle }$ und
$-1=\sum _{i=2}^{\infty }\lambda ^{i}+1\;=\;{\bar {1}}01{_{_{\blacktriangleleft }}}{_{_{\lambda }}}\;=\;\dots 11101{_{_{\blacktriangleleft }}}{_{_{\lambda }}}$	im System ${\big \langle }\lambda ={\mathrm i}\!+\!1;\{0,1,\varepsilon ^{4},\varepsilon ^{2}\}{\big \rangle }$ .

Die folgende Funktion $\operatorname {EncodeNonarch} _{R}$ kann im nichtarchimedischen Kontext alle Quaternionen aus ${\hat {H}}$ beliebig genau codieren, auch solche die keine endlichen Codierungen haben (deshalb die Erweiterung um die maximale Stellenzahl gegenüber der archimedischen Funktion).

$\operatorname {EncodeNonarch} _{R}(\xi ,s)\;\{$	Quaternion $\xi \in {\hat H}$ , maximale Stellenzahl $s\in \mathbb{N}$
" "	die leere Zeichenkette
${\mathrm {for}}\;j=1\;{\mathrm {to}}\;s\;\{\;$
${\mathrm {if}}\;\xi =0\;{\mathrm {then}}\;{\mathrm {return}}\;[{\mathrm {true}},D]\;$	Das Ergebnis ist vollständig.
${\mathrm {for}}\;k=0\;{\mathrm {to}}\;3\;\{\;$	Genau eine der Ziffern aus dem 4-wertigen …
$\eta =\xi -C[k]$	… Ziffernsatz qualifiziert sich.
${\mathrm {if}}\;{\mathrm {mod}}(\\|\eta \\|,2)=0\;{\mathrm {then}}\;\{\;$	Wenn die Norm gerade ist, …
$\xi =\eta \cdot \lambda ^{{-1}}$	… ist diese Division (eine rechte) ohne Rest.
	Das Zeichen für die neue Ziffer …
	… wird dem Ergebnis links vorangestellt.
${\mathrm {break}}\;\}\}\}$
${\mathrm {return}}\;[{\mathrm {false}},D]\;\}$	Das Ergebnis ist nicht vollständig.

Die für den archimedischen Fall genannten Codierungssysteme sind auch für ${\hat {H}}$ (und $\operatorname {EncodeNonarch} _{R}$ ) geeignet, insbesondere da die $\varrho$ Primelemente in ${\hat {H}}$ sind und so als Basis $\lambda$ genommen werden können.
Sind für ein $\xi \in H$ nichtarchimedische und archimedische Codierung (bei gleichem System) beide endlich, dann stimmen auch die Codes überein.

↑ Die Sonderstellung der 2 unter den Primzahlen kommt auch bei den folgenden Überlegungen zur Nullteilerfreiheit von vollständigen, umfassenden Algebren heraus: Sei eine ungerade Primzahl. Nach dem Vier-Quadrate-Satz gibt es 4 Summanden mit . Nun ist quadratischer Rest , es gibt also nach dem henselschen Lemma ein mit , so dass . Mit dem Ergebnis, dass es unter den Quaternionen mit p-adischen Koeffizienten für Nullteiler gibt.
- Für alle ungeraden Zahlen ist $n^{2}\equiv 1\;\operatorname {mod}\,8$ , also ist die Summe von 1 bis 4 ungeraden Quadraten $\not \equiv 0\;\operatorname {mod}\,8$ . Somit gibt es keine 4 Quadrate in $\mathbb {Q} _{2}$ , die nicht-trivial zu $0$ aufsummieren, ${\hat S}$ enthält also keine Nullteiler – wie es sein muss.
- Schon bei 5 Summanden sieht es ganz anders aus:
Alle $n\equiv 7\;\operatorname {mod}\,8$ benötigen wenigstens 4 Summanden $n_{1},n_{2},n_{3},n_{4}\in \mathbb {N}$ , damit ihre Quadrate die Summe bilden. Andererseits ist $-n\equiv 1\;\operatorname {mod}\,8$ quadratischer Rest $\;\operatorname {mod}\,8$ , es gibt also ein $m_{2}\in \mathbb{N}$ mit $m_{2}^{2}\equiv -n\;\operatorname {mod}\,2^{3}$ . Für $i=2,3,4,\dots$ sei nun $m_{i}\in \mathbb{N}$ derart, dass $m_{i}^{2}\equiv -n\;\operatorname {mod}\,2^{{i+1}}$ , und sei $m_{{i+1}}\equiv m_{i}-{\tfrac {m_{i}^{2}+n}{2m_{i}}}\;\operatorname {mod}\,2^{{i+2}}$ . Dann ist $m_{{i+1}}^{2}\equiv m_{i}^{2}-(m_{i}^{2}+n)$ $\equiv -n\;\operatorname {mod}\,2^{{i+2}}$ , d.h., es gibt eine $\operatorname {d}_{2}$ -konvergente Folge $m:=\lim _{{i\to \infty }}m_{i}\in \mathbb{Z } _{2}$ , deren Quadrat ist. Mit dem Ergebnis, dass die Summe aus den 5 Quadraten $n_{1}^{2}+n_{2}^{2}+n_{3}^{2}+n_{4}^{2}+m^{2}$ verschwindet.
Alle $n\equiv 3\;\operatorname {mod}\,8$ oder $n\equiv 6\;\operatorname {mod}\,8$ benötigen wenigstens 3 Summanden $n_{1},n_{2},n_{3}\in \mathbb{N}$ , damit ihre Quadrate die Summe bilden. Andererseits sind weder $-n\equiv 5\;\operatorname {mod}\,8$ noch $-n\equiv 2\;\operatorname {mod}\,8$ quadratische Reste $\;\operatorname {mod}\,8$ , es braucht also mindestens 2 zusätzliche Zahlen $n_{4}$ und $n_{5}$ für $n_{4}^{2}+n_{5}^{2}\equiv -n\;\operatorname {mod}\,8$ . Wie oben kann $n_{5}\in \mathbb{Z } _{2}$ so gewählt werden, dass $n_{1}^{2}+n_{2}^{2}+n_{3}^{2}+n_{4}^{2}+n_{5}^{2}$ verschwindet.
- Aus jedem dieser Ergebnisse folgt weiter, dass es in den Quaternionenalgebren mit Koeffizienten aus den über $\mathbb {Q} _{2}$ quadratischen Körpern $\mathbb{Q} _{2}({\sqrt {-1}})$ , $\mathbb{Q} _{2}({\sqrt {\pm 2}})$ , $\mathbb{Q} _{2}({\sqrt {\pm 3}})$ und $\mathbb{Q} _{2}({\sqrt {\pm 6}})$ (die Aufzählung ist vollständig) Nullteiler gibt.
- Nullteiler gibt es auch unter den Quaternionen mit Koeffizienten aus dem über $\mathbb {R}$ quadratischen Körper $\mathbb {C} =\mathbb {R} (\mathrm {i} _{\mathbb {C} })$ wegen der Quadratsumme $\mathrm {i} _{\mathbb {C} }^{2}+1^{2}+0^{2}+0^{2}=0$ .
Solche Erweiterungen einer Quaternionenalgebra werden als Skalarerweiterungen bezeichnet. Durch sie können im Tensorring Nullteiler hinzukommen. Wegen und sind weder 120-Zeller noch 600-Zeller Polytope des . Nach Conway, 3.5 The Finite Groups of Quaternions, Seite 33, sind alle Quaternionen über , die endliche Ordnung haben, in .

Basierend auf einem Artikel in:

Wikipedia.de