
Kreuzpolytop
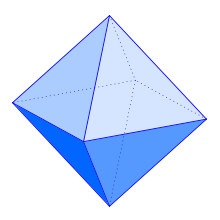
Ein Kreuzpolytop oder Hyperoktaeder ist in der Geometrie ein Polytop, das eine
Verallgemeinerung eines Oktaeders
vom dreidimensionalen
Raum auf Räume beliebiger Dimension
darstellt. Ein Kreuzpolytop im -dimensionalen
Raum ist die konvexe
Hülle von
Strecken,
die sich alle in einem gemeinsamen Kreuzungspunkt schneiden. Bei einem
regulären Kreuzpolytop sind diese Strecken alle gleich lang und schneiden
sich jeweils zentral und rechtwinklig.
Die Symmetriegruppe
eines regulären Kreuzpolytops ist die Hyperoktaedergruppe.
Neben Hyperwürfeln
und regulären Simplizes
sind reguläre Kreuzpolytope die einzigen regulären
Polytope, die in beliebigen Dimensionen existieren. Kreuzpolytope finden
Anwendung unter anderem in der linearen
Optimierung.
Einheits-Kreuzpolytop
.png)
Definition
Das -dimensionale
Einheits-Kreuzpolytop ist die konvexe
Hülle der
Ecken
:
.
Dabei bezeichnet
den
-ten
Einheitsvektor des Vektorraums
.
Beispiele
- Das eindimensionale Einheits-Kreuzpolytop ist das abgeschlossene Einheitsintervall
.
- Das zweidimensionale Einheits-Kreuzpolytop ist ein (auf die Spitze gestelltes) Quadrat.
- Das dreidimensionale Einheits-Kreuzpolytop ist ein Oktaeder und damit einer der platonischen Körper.
Darstellung
Das Einheits-Kreuzpolytop lässt sich auch folgendermaßen als Punktmenge im
-dimensionalen
Raum darstellen:
.
Das Einheits-Kreuzpolytop ist damit die Einheitskugel
bezüglich der Summennorm
.
Diese Betragsungleichung lässt sich auch als System von
linearen Ungleichungen umschreiben. Daher wird das Einheits-Kreuzpolytop durch
genau
Hyperebenen begrenzt.
Komponenten
Das Einheits-Kreuzpolytop ist konvex, abgeschlossen und zusammenhängend (bezüglich der euklidischen Metrik). Es besteht aus folgenden Komponenten:
- Es hat
Ecken, eben die (positiven und negativen) Einheitsvektoren.
- Es hat
Kanten, denn jede Ecke
ist außer mit der gegenüberliegenden Ecke
mit jeder anderen über eine Kante verbunden.
- Es hat
Facetten, die Simplizes des
sind.
Allgemein besteht das Einheits-Kreuzpolytop aus
Komponenten der Dimension .
Symmetrien
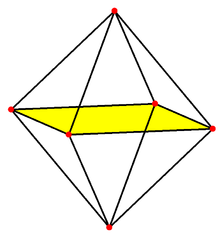
Das Einheits-Kreuzpolytop ist punktsymmetrisch
bezüglich des Koordinatenursprungs,
das heißt, für alle
gilt
.
Weiterhin ist es symmetrisch bezüglich Spiegelungen an den Koordinatenebenen, das heißt,
für .
Die
Koordinatenebenen zerteilen dabei das Einheits-Kreuzpolytop in
Einheitssimplizes
des
.
Volumen
Das -dimensionale
Volumen des
Einheits-Kreuzpolytops beträgt
.
Das Volumen wird daher für wachsende Dimension beliebig klein.
Reguläre Kreuzpolytope
Definition
Ein reguläres Kreuzpolytop ist ein Polytop, das aus dem Einheits-Kreuzpolytop
durch Skalierung,
Drehung,
Parallelverschiebung oder
Koordinatentransformation
hervorgeht. Ein Polytop
ist demnach ein reguläres Kreuzpolytop, wenn es eine reelle Zahl
,
eine orthogonale
Matrix
und einen Vektor
gibt, sodass
gilt.
Eigenschaften
Reguläre Kreuzpolytope haben dieselbe Anzahl von Ecken, Kanten und Facetten
wie das Einheits-Kreuzpolytop. Sie besitzen auch die gleichen
Symmetrieeigenschaften, lediglich das Symmetriezentrum und die Spiegelebenen
werden entsprechend mittransformiert. Auch die Volumenformel bleibt erhalten und
erhält lediglich einen zusätzlichen Faktor :
.
Kreuzpolytop (oder Hyperoktaeder) und Maßpolytop (oder Hyperwürfel) sind zueinander dual. Daher stimmen auch ihre Symmetriegruppen überein.
Allgemeine Kreuzpolytope
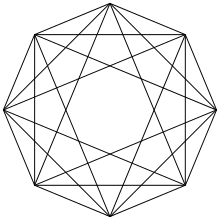
Definition
Allgemein werden alle Polytope, die zum Einheits-Kreuzpolytop kombinatorisch äquivalent sind, Kreuzpolytope genannt. Präzise formuliert bedeutet das:
- Ein Polytop
heißt Kreuzpolytop, wenn es eine Bijektion
von der Menge der Ecken von
auf die Menge der Ecken
eines Einheits-Kreuzpolytops
gibt, sodass zwei Ecken
und
von
genau dann durch eine Kante verbunden sind, wenn
und
dies in
sind.
Eigenschaften
Ein allgemeines Kreuzpolytop hat dieselbe Anzahl von Ecken, Kanten und Facetten wie das Einheits-Kreuzpolytop, doch die Symmetrien gehen verloren.
Verwendung
Das Kreuzpolytop gilt als Prototyp eines Polytops, das (in Relation zur
Dimension) sehr wenige Ecken, aber sehr viele Facetten besitzt. Diese
Eigenschaft ist in der linearen Optimierung besonders wichtig, da der Simplex-Algorithmus,
das Standardverfahren zur Lösung linearer Optimierungsprobleme, gezielt Ecken
auf ihre Optimalität prüft. Das Gegenstück hierzu ist der Hyperwürfel, dessen
Eckenzahl exponentiell, die Facettenzahl aber nur linear in
anwächst.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 05.01. 2020