
Volumen
| Physikalische Größe | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Name | Volumen Rauminhalt | ||||||||||||
| Formelzeichen | |||||||||||||
| Abgeleitet von | Länge | ||||||||||||
| |||||||||||||
Das Volumen (Pl. Volumen oder Volumina; von lat. volumen „Windung, Krümmung“, aus volvere „wälzen, rollen“), auch: Raum- oder Kubikinhalt, ist der räumliche Inhalt eines geometrischen Körpers. Übliches Formelzeichen ist V.
In der Physik bezeichnet man mit dem Volumen die Ausdehnung (den Platzbedarf) eines Körpers. Die (kohärente) SI-Einheit für das Raummaß ist der Kubikmeter (Einheitenzeichen m3). Vereinzelt liest man noch die veralteten Abkürzungen cbm für m³ und ccm für cm³. Die Einheit Liter ist für Gase und Flüssigkeiten gebräuchlich und als 1 dm3 (10×10×10 cm³) definiert.
Technisch muss unterschieden werden:
- Hohlvolumen, der freie Raum innerhalb gewisser Grenzen, etwa das Fassungsvermögen eines Behälters
- Rauminhalt, das Volumen fester Körper, von Flüssigkeiten oder Gasen
Geschichte
Die ersten bekannten Formeln zur Volumenbestimmung (auch Stereometrie) stammen schon aus dem frühen Ägypten. Das Moskauer Papyrus ist eine Sammlung von Rechenaufgaben und ist etwa auf das Jahr 1850 v. Chr. datiert. Unter anderem sind hier die Formeln für die Bestimmung der Volumina für Rechteckkegel beschrieben. Die Bestimmung wurde durch Analyse und anschließender Synthese erreicht. Das heißt, der Körper wurde in mehrere bekannte Körper zerlegt und die Einzelvolumina addiert.
Messmethoden
Im Laufe der Zeit haben sich ganz unterschiedliche Methoden zur Bestimmung von Volumina entwickelt:
- Auslitern: Der Körper wird mit Sand oder Wasser gefüllt, dessen Menge anschließend in einem bekannten Gefäß bestimmt wird; somit lässt sich bei Gefäßen das Volumen ihres Innenraumes bestimmen.
- Wasserverdrängung: Der Körper wird in ein vollständig mit Wasser gefülltes Gefäß eingetaucht. Das Volumen des übertretenden Wassers wird anschließend in einem geometrisch einfachen Gefäß (z.B. Zylinder) vermessen. Infolge möglicher Wechselwirkungen zwischen Probekörper und Wasser kann es zu Messfehlern kommen, weshalb auch andere Flüssigkeiten eingesetzt werden können.
- Bei einem Körper mit einer bekannten Dichte lässt sich das Volumen auch erwiegen.
Volumen-Berechnung
Mathematisch gesehen ist das Volumen (der Rauminhalt) ein Maß für eine
messbare Teilmenge
des gewöhnlichen dreidimensionalen Raums. Im Allgemeinen lässt sich das Volumen
eines Körpers (Bereich
im
)
durch ein 3-fach-Integral
beschreiben. Solche Integrale können sehr schwierig oder nur numerisch lösbar
sein. Bei vielen einfachen Fällen (Polyeder) lässt sich das Volumen ohne
Integrale bestimmen. Bei Rotationskörper und solchen mit stetigen
Querschnittsflächen (s. Tabelle) kommt man mit einfachen Integralen aus. Hier
die Volumina einiger häufig vorkommender Körper:
| Körper | Volumen | Parameter |
|---|---|---|
| Würfel | 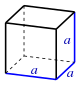 | |
| Quader | 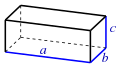 | |
| Prisma (Grundfläche G) |
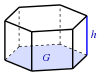 | |
| Pyramide (Grundfläche G) |
 | |
| Kugel |  | |
| Ellipsoid | 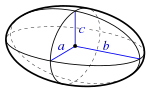 | |
| senkrechter Kreiszylinder | 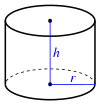 | |
| senkrechter Kreiskegel | 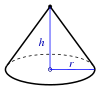 | |
| Torus |  | |
| Rotationskörper |  | |
| Körper mit stetiger
Querschnittsfläche (z.B. Steinmetz-Körper) |
Für den Rotationskörper ist |
Verallgemeinerung
Man kann ein Volumen auch über mehrdimensionale Mannigfaltigkeiten
definieren, siehe dazu auch Volumenform.
Nach dieser Verallgemeinerung ist das Volumen eines Teilraumes des
zweidimensionalen euklidischen Raumes sein Flächeninhalt und Entsprechendes gilt
auch in höherdimensionalen euklidischen Räumen. Beispielsweise hat ein
n-dimensionaler Hyperwürfel
mit Kantenlänge
ein Volumen von
.
Das Volumen einer orientierbaren Riemannschen Mannigfaltigkeit ist definiert durch Integration der Volumenform über die Mannigfaltigkeit.
Hohlraum
Ein Hohlraum ist ein mathematisches, ein physikalisches oder ein natürliches Objekt. Ein Hohlraum hat ein Volumen, das man als Hohlvolumen bezeichnet. Ein in einer Struktur eingeschlossenes Volumen kann ein Hohlraum sein. Dabei verändert die Existenz von Hohlräumen oft die umliegende Struktur, z.B. in Hinsicht auf Festigkeit oder Elastizität (Siehe Porosität).
Ein natürlicher Hohlraum enthält ein Vakuum oder ist mit Gasen, Flüssigkeiten oder anderen Stoffen gefüllt, was wiederum die umschließende Struktur beeinflussen kann. Insbesondere kann die Grenzfläche zwischen Hohlraum und Struktur sich verändern, schwer zu erkennen sein oder auch nur auf gedanklicher Ebene existieren. Auch ein Hohlraum, der eine oder mehrere Öffnungen hat, also nicht vollständig von der umschließenden Struktur umgeben ist, wird umgangssprachlich so bezeichnet.
Die Größe des umschlossenen Volumens kann oft errechnet oder experimentell bestimmt werden. In manchen Fällen ist dies allerdings prinzipiell nicht möglich.
Hohlraumbildung ist ein oft auftretendes Phänomen bei geologischen und sonstigen physikalischen und chemischen Prozessen.
Evakuierte Hohlräume haben mehrere universelle Eigenschaften, eine davon ist die Hohlraumstrahlung.
Beispiele: Hohlraum
- … als Gefäß: Flasche, Tank, Verdauungssystem, Schwamm
- … als Aufenthaltsort: Wohnung, Höhle
- … als Ergebnis chemischer oder physikalischer Vorgänge: Luftblase, Seifenblase, „Löcher“ im Käse, Lunker
Siehe auch
- Banach-Tarski-Paradoxon und Maßtheorie, zu den Grenzen des Volumenbegriffs der Mathematik bei Verwendung in der tatsächlichen Welt


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 25.12. 2022