Kugel

Bild einer Kugel mit Längen- und Breitenkreisen

Eine Kugel ist in der Geometrie die Kurzbezeichnung für Kugelfläche oder Kugelkörper.

Kugelfläche und Kugelkörper

Die Kugelfläche ist die bei der Drehung einer Kreislinie um einen Kreisdurchmesser entstehende Fläche. Sie ist eine Rotationsfläche sowie eine spezielle Fläche zweiter Ordnung und wird beschrieben als die Menge (der geometrische Ort) aller Punkte im dreidimensionalen euklidischen Raum, deren Abstand von einem festen Punkt des Raumes gleich einer gegebenen positiven reellen Zahl $\!\ r$ ist. Der feste Punkt wird als Mittelpunkt oder Zentrum der Kugel bezeichnet, die Zahl $\!\ r$ als Radius der Kugel.

Die Kugelfläche teilt den Raum in zwei getrennte offene Untermengen, von denen genau eine konvex ist. Diese Menge heißt das Innere der Kugel. Die Vereinigungsmenge einer Kugelfläche und ihres Inneren heißt Kugelkörper oder Vollkugel. Die Kugelfläche wird auch Kugeloberfläche oder Sphäre genannt.

Sowohl Kugelfläche als auch Kugelkörper werden oft kurz als Kugel bezeichnet, wobei aus dem Zusammenhang klar sein muss, welche der beiden Bedeutungen gemeint ist.

Eine Kugelfläche mit Mittelpunkt ( $\!\ x_{0}$ , $\!\ y_{0}$ , $\!\ z_{0}$ ) und Radius $\!\ r$ ist die Menge aller Punkte ( $\!\ x$ , $\!\ y$ , $\!\ z$ ), für die

$\!\ (x-x_{0})^{2}+(y-y_{0})^{2}+(z-z_{0})^{2}=r^{2}$

erfüllt ist.

Kugelkoordinaten und kartesisches Koordinatensystem

In Vektorschreibweise mit ${\vec {x}}={\begin{pmatrix}x\\y\\z\end{pmatrix}}$ , ${\vec {m}}={\begin{pmatrix}x_{0}\\y_{0}\\z_{0}\end{pmatrix}}$ :

$({\vec {x}}-{\vec {m}})\cdot ({\vec {x}}-{\vec {m}})=r^{2}$ ,

$(\vec x - \vec m )^2 = r^2$ ,

$|{\vec {x}}-{\vec {m}}|^{2}=r^{2}$ oder

$|{\vec {x}}-{\vec {m}}|=r$ .

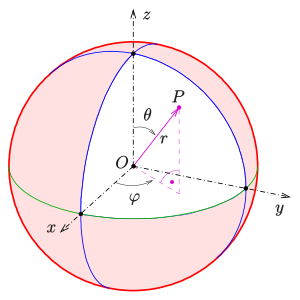
Die Punkte auf der Kugelfläche mit dem Radius $\!\ r$ und dem Zentrum im Ursprung können durch Kugelkoordinaten wie folgt parametrisiert werden:

$x=r\cdot \sin \theta \cdot \cos \varphi$

$y=r\cdot \sin \theta \cdot \sin \varphi$

$z=r\cdot \cos \theta$

mit $0\leq \theta \leq \pi$ und $0\leq \varphi <2\pi$ .

Kugelschnitte

Bringt man eine Ebene mit einer Kugel zum Schnitt, entsteht immer ein Kreis. Wenn die Ebene den Mittelpunkt der Kugel enthält, nennt man die Schnittlinie Großkreis, andernfalls Kleinkreis.
Die beiden dabei entstehenden Teilkörper heißen Kugelabschnitt oder Kugelsegment, im Falle des Großkreises Halbkugel (Hemisphäre).
Der gekrümmte Teil der Oberfläche eines Kugelsegments wird Kugelkappe, Kugelhaube oder Kugelkalotte genannt.
Ein Kugelsegment und der Kegel mit dem Schnittkreis als Basis und dem Kugelmittelpunkt als Spitze ergeben einen Kugelausschnitt oder Kugelsektor.
Zwei parallele, die Kugel schneidende (nicht berührende) Ebenen schneiden aus der Kugel eine Kugelschicht heraus. Den gekrümmten Teil der Oberfläche einer Kugelschicht bezeichnet man als Kugelzone.
Zwei sich schneidende Ebenen, deren Schnittgerade teilweise innerhalb der Kugel liegt, schneiden aus der Kugel ein Objekt, dessen gekrümmte Oberfläche das Kugelzweieck ist.
Eine Kugelschale (Hohlkugel) ist die Differenzmenge zweier konzentrischer Kugeln mit unterschiedlichem Radius.

Kurven auf einer Kugel

Ebener Schnitt einer Kugel

Schnitt Kugel – Zylinder: 2 Kreise

Kreise

Der Schnitt einer Ebene mit einer Kugel ist ein Kreis, ein Punkt oder leer.

Ist der Schnitt ein Kreis, so lässt er sich in Parameterform $\;{\vec {x}}=({\vec {e}}_{0}+{\vec {e}}_{1}\cos t+{\vec {e}}_{2}\sin t)^{T}\;$ darstellen.

Allerdings kann eine Kugel auch kompliziertere Flächen in einem Kreis schneiden:

Ein nicht leerer Schnitt einer Kugel mit einer Rotationsfläche, deren Achse durch den Mittelpunkt der Kugel geht, besteht aus Kreisen und/oder Punkten.

Im Bild schneidet eine Kugel einen Zylinder in zwei Kreisen. Wäre der Radius des Zylinders gleich dem Kugelradius, bestünde der Schnitt aus einem Berührkreis. Ein Rotations-Ellipsoid mit demselben Mittelpunkt wie die Kugel und dem Kugelradius als großer Halbachse würde die Kugel in zwei Punkten (Scheiteln) berühren.

Diese Eigenschaft wird in der darstellenden Geometrie zur Konstruktion von Punkten der Schnittkurve von Rotationsflächen verwendet.

Kugelspirale mit $c=8$

Clelia-Kurven

Ist die Kugel in Parameterform

${\vec {x}}=(r\cos \theta \cos \varphi ,r\cos \theta \sin \varphi ,r\sin \theta )^{T}$

gegeben, so erhält man Clelia-Kurven, wenn man

$\varphi =c\;\theta \;,\ c>0\;,$

setzt. Spezialfälle davon sind: vivianische Kurven ( $c=1$ ) und Kugelspiralen ( $c>2$ ).

Loxodrome

Die Kurve auf der Erdkugel, welche die Meridiane (Längskreise) immer unter dem gleichen Winkel schneidet, ist eine Loxodrome. Sie schlingt sich spiralartig um die Pole, die ihre beiden asymptotischen Punkte sind, d.h. sie enthält nicht die Pole. Sie ist keine Kugelspirale im obigen Sinne. Es besteht kein einfacher Zusammenhang zwischen den Winkeln $\varphi$ und $\theta$ .

Schnitte mit anderen Quadriken

Schnittkurve Kugel-Zylinder

Wird eine Kugel von einer anderen Quadrik (Zylinder, Kegel …) geschnitten, so entstehen bei geeigneten Radien, Parameter … Schnittkurven.

Beispiel: Kugel – Zylinder

Die Schnittkurve der Kugel mit der Gleichung $\;x^{2}+y^{2}+z^{2}=r^{2}\;$ und dem Zylinder mit der Gleichung $\;(y-y_{0})^{2}+z^{2}=a^{2}\;$ besteht aus den Lösungen des nicht linearen Gleichungssystems

$x^{2}+y^{2}+z^{2}-r^{2}=0$

$(y-y_{0})^{2}+z^{2}-a^{2}=0\ .$

(s. implizite Kurve, Bild)

Formeln

Formeln zur Kugel
Geometrische Größe	Formel
Kugelradius	$\!\ r$
Kugeldurchmesser	$\!\ d=2r$
Umfang (Großkreis)	IMG class="text" style="width: 23.4ex; height: 5.5ex; vertical-align: -2ex;" alt="U=2\pi r=\pi d\ {\color {OliveGreen}={\frac {\mathrm {d} A_{\mathrm {PF} }}{\mathrm {d} r}}}" src="/svg/f3a46bc2d18673c37610c97f0b67b008421c8107.svg">
Volumen	$V={\frac {4}{3}}\pi r^{3}={\frac {1}{6}}\pi d^{3}=\int _{-r}^{r}\left(r^{2}-x^{2}\right)\pi \mathrm {d} x$
Oberfläche	$A_{O}=4\pi r^{2}=\pi d^{2}\ {\color {OliveGreen}={\frac {\mathrm {d} V}{\mathrm {d} r}}}$
Projektionsfläche/Kugelquerschnitt	$A_{\mathrm {PF} }=\pi r^{2}=\int _{0}^{r}U\mathrm {d} r$
Höhe (Kugelsegment/-kalotte, Kugelschicht, nicht mit dem h in der Skizze unten identisch)	$\!\ h$
Volumen einer Kugelkalotte	$V_{\mathrm {KK} }={\frac {\pi h^{2}}{3}}(3r-h)$
Flächeninhalt einer Kugelkalotte	$A_{\mathrm {KK} }=2\pi rh=2\pi r^{2}\left(1-\cos {\frac {\alpha }{2}}\right)$
Mantelfläche einer Kugelschicht	$A_{\mathrm {KS} }=2\pi rh=2\pi r^{2}\int _{\alpha }^{\beta }\sin x\,\mathrm {d} x$
Trägheitsmoment einer Hohlkugel (Drehachse durch Mittelpunkt)	$J={\frac {2}{3}}mr^{2}$
Trägheitsmoment einer Vollkugel (Drehachse durch Mittelpunkt)	$J={\frac {2}{5}}mr^{2}$

Volumen

Das Kugelvolumen ist der Rauminhalt einer Kugel, der durch die Kugeloberfläche begrenzt wird.

Kegelherleitung (archimedische Herleitung)

Herleitung des Kugelvolumens nach Cavalieri

Nach einer Überlegung des griechischen Mathematikers Archimedes gibt es zu einer Halbkugel mit Radius $\!\ r$ einen Vergleichskörper, dessen Volumen mit dem der Halbkugel übereinstimmt, aber einfach zu berechnen ist. Dieser Vergleichskörper entsteht dadurch, dass man aus einem Zylinder (genauer: einem geraden Kreiszylinder) mit Grundflächenradius $\!\ r$ und Höhe $\!\ r$ einen Kegel (genauer: einen geraden Kreiskegel) mit Grundflächenradius $\!\ r$ und Höhe $\!\ r$ entfernt.

Zum Nachweis, dass die Halbkugel und der Vergleichskörper gleiches Volumen haben, kann man das Prinzip von Cavalieri heranziehen. Dieses Prinzip beruht auf der Idee, die betrachteten Körper in unendlich viele Scheiben infinitesimaler (unendlich kleiner) Dicke zu zerlegen. (Eine Alternative zu diesem Verfahren wäre die Anwendung der Integralrechnung.) Nach dem erwähnten Prinzip untersucht man für beide Körper die Schnittflächen mit den Ebenen, die zur jeweiligen Grundfläche parallel sind und von dieser einen vorgegebenen Abstand $\!\ h$ haben.

Im Falle der Halbkugel ist die Schnittfläche eine Kreisfläche. Der Radius $\!\ s$ dieser Kreisfläche ergibt sich aus dem Satz des Pythagoras:

$s^{2}+h^{2}\,=\,r^{2}$ .

Damit erhält man für den Inhalt der Schnittfläche

$A_{1}\,=\,\pi s^{2}=\pi (r^{2}-h^{2})=\pi r^{2}-\pi h^{2}$ .

Im Falle des Vergleichskörpers ist die Schnittfläche dagegen ein Kreisring mit Außenradius $\!\ r$ und Innenradius $\!\ h$ . Der Flächeninhalt dieser Schnittfläche ist demzufolge

$A_{2}\,=\,\pi r^{2}-\pi h^{2}$ .

Für einen beliebigen Abstand $\!\ h$ zur Grundfläche stimmen die beiden Schnittflächen also im Flächeninhalt überein. Damit folgt mit dem Prinzip von Cavalieri, dass die Halbkugel und der Vergleichskörper das gleiche Volumen haben.

Das Volumen des Vergleichskörpers und damit auch der Halbkugel lässt sich nun leicht berechnen:

Man subtrahiert vom Zylindervolumen das Kegelvolumen.

$V_{\text{Zylinder}}=\pi r^{2}\cdot r=\pi r^{3}$

$V_{\text{Kegel}}={\frac {1}{3}}\pi r^{2}\cdot r={\frac {1}{3}}\pi r^{3}$

$V_{\text{Halbkugel}}=V_{\text{Vergleichskörper}}\,=\pi r^{3}-{\frac {1}{3}}\pi r^{3}={\frac {2}{3}}\pi r^{3}$

Daher gilt für das Volumen der (Voll-)Kugel:

$V_{\text{Kugel}}\,=\,2\cdot V_{\text{Halbkugel}}={\frac {4}{3}}\pi r^{3}$ .

Alternative Herleitung

Die Kugel kann in unendlich viele Pyramiden mit der Höhe $\!\ r$ zerteilt werden (Spitzen im Mittelpunkt der Kugel), deren gesamte Grundfläche der Oberfläche der Kugel (siehe weiter unten) entspricht. Damit beträgt das gesamte Volumen aller Pyramiden: $V={\frac {O\,r}{3}}={\frac {(4\pi r^{2})r}{3}}={\frac {4}{3}}\pi r^{3}$ .

Herleitung mit Hilfe der Integralrechnung

Radius im Abstand $\!\ x$ :

$s={\sqrt {r^{2}-x^{2}}}$ .

Kreisfläche im Abstand $\!\ x$ :

$\!\ A_{x}=\pi s^{2}$ .

Volumen der Kugel $\!\ V$ :

$V=\int _{-r}^{r}{A_{x}\,\mathrm {d} x}=\int _{-r}^{r}{\pi s^{2}\,\mathrm {d} x}=\int _{-r}^{r}{\left({r^{2}-x^{2}}\right)}\pi \,\mathrm {d} x=\int _{-r}^{r}\pi {r^{2}}\,\mathrm {d} x-\int _{-r}^{r}\pi {x^{2}}\,\mathrm {d} x$

$V=\pi r^{2}\left[x\right]_{-r}^{r}-{\frac {1}{3}}\pi \left[{x^{3}}\right]_{-r}^{r}$

$V=\pi r^{2}\left[r-(-r)\right]-{\frac {1}{3}}\pi \left[r^{3}-(-r)^{3}\right]=2\pi r^{3}-{\frac {2}{3}}\pi r^{3}={\frac {4}{3}}\pi r^{3}$ .

Auf die gleiche Art kann man das Volumen eines Kugelsegments $\!\ V_{\mathrm {KS} }$ der Höhe $\!\ h$ berechnen:

$V_{\mathrm {KS} }=\int _{r-h}^{r}{A_{x}\,\mathrm {d} x}=\pi r^{2}\left[x\right]_{r-h}^{r}-{\frac {1}{3}}\pi \left[{x^{3}}\right]_{r-h}^{r}$

$V_{\mathrm {KS} }=\pi r^{2}\left[r-(r-h)\right]-{\frac {1}{3}}\pi \left[r^{3}-(r-h)^{3}\right]=\pi r^{2}h-{\frac {1}{3}}\pi \left[r^{3}-(r^{3}-3r^{2}h+3rh^{2}-h^{3})\right]$

$V_{\mathrm {KS} }=\pi r^{2}h-\pi r^{2}h+\pi rh^{2}-{\frac {1}{3}}\pi h^{3}={\frac {\pi h^{2}}{3}}(3r-h)$ .

Weitere Herleitungen

Eine Kugel mit Radius , deren Mittelpunkt im Koordinatenursprung liegt, lässt sich durch die Gleichung

$K:~x^{2}+y^{2}+z^{2}\leq R^{2}$

beschreiben, wobei $x,\ y,\ z$ die Raumkoordinaten sind.

Über die Integralrechnung lässt sich dieses Problem auf zwei Arten lösen:

Wir parametrisieren die Kugel bis auf eine Lebesgue-Nullmenge durch

${\begin{pmatrix}x\\y\\z\end{pmatrix}}={\begin{pmatrix}r~\sin \vartheta ~\cos \varphi \\r~\sin \vartheta ~\sin \varphi \\r~\cos \vartheta \end{pmatrix}}\qquad (0\leq r\leq R,\ 0\leq \vartheta \leq \pi ,\ 0\leq \varphi \leq 2\pi )$ .

Mit der Funktionaldeterminante

$\det {\frac {\partial (x,y,z)}{\partial (r,\vartheta ,\varphi )}}=r^{2}\sin \vartheta$

ergibt sich das benötigte Volumenelement $\!\ \mathrm {d} V$ als

$\mathrm {d} V=r^{2}\sin \vartheta \;\mathrm {d} r\,\mathrm {d} \varphi \,\mathrm {d} \vartheta$ .

Das Volumen der Kugel ergibt sich daher als

${\begin{aligned}\int _{K}\mathrm {d} V&=\int _{0}^{\pi }\int _{0}^{2\pi }\int _{0}^{R}r^{2}\sin \vartheta \;\mathrm {d} r\,\mathrm {d} \varphi \,\mathrm {d} \vartheta \\&=\int _{0}^{R}r^{2}\mathrm {d} r\int _{0}^{2\pi }\mathrm {d} \varphi \int _{0}^{\pi }\sin \vartheta \;\mathrm {d} \vartheta \\&={\frac {R^{3}}{3}}\cdot 2\pi \cdot 2\\&={\frac {4}{3}}\pi R^{3}.\\\end{aligned}}$

Eine weitere Möglichkeit besteht über die Polarkoordinaten:

${\begin{aligned}\int _{K}\!\mathrm {d} V&=\iint \limits _{x^{2}+y^{2}\leq R^{2}}\left(\int \limits _{-{\sqrt {R^{2}-x^{2}-y^{2}}}}^{\sqrt {R^{2}-x^{2}-y^{2}}}\mathrm {d} z\right)\mathrm {d} y\,\mathrm {d} x\\&=\iint \limits _{x^{2}+y^{2}\leq R^{2}}2{\sqrt {R^{2}-x^{2}-y^{2}}}\,\mathrm {d} y\,\mathrm {d} x.\end{aligned}}$

Nun wird das kartesische Koordinatensystem in das Polarkoordinatensystem transformiert, was bedeutet, dass die Integration nach dem „Wechsel“ des Koordinatensystems mittels der Variablen $\!\varphi$ und $\!r$ fortgeführt wird, anstatt wie zuvor durch $\!x$ und $\!y$ . Motivation dieser Transformation ist die erhebliche Vereinfachung der Rechnung im weiteren Verlauf. Für das Differential bedeutet das: $\mathrm {d} y\,\mathrm {d} x\;{\xrightarrow {\text{wird zu}}}\;r\,\mathrm {d} r\,\mathrm {d} \varphi$ (Stichwort: Flächenelement)

${\begin{aligned}\int _{K}\!\mathrm {d} V&=\int \limits _{0}^{2\pi }\int \limits _{0}^{R}2{\sqrt {R^{2}-r^{2}}}\;r\,\mathrm {d} r\,\mathrm {d} \varphi \\&=2\pi \int \limits _{0}^{R}2{\sqrt {R^{2}-r^{2}}}\;r\,\mathrm {d} r\\&=2\pi (-1){\frac {2}{3}}\left[{\sqrt {(R^{2}-r^{2})^{3}}}\right]_{r=0}^{R}\\&={\frac {4}{3}}\pi R^{3}.\end{aligned}}$

Weiterer Weg mit Hilfe der Formel für Rotationskörper

Lässt man ein Flächenstück um eine feste Raumachse rotieren, erhält man einen Körper mit einem bestimmten Volumen. Bei einer Kreisfläche entsteht so eine Kugel. Anschaulich kann man sich das als eine rotierende Münze vorstellen.

Die allgemeine Formel für Rotationskörper, die um die x-Achse rotieren, ergibt

$V=\pi \int _{a}^{b}[f(x)]^{2}\mathrm {d} x=\pi \int _{a}^{b}y^{2}\,\mathrm {d} x$ .

Die Gleichung für den Kreis ist

$(x-x_{M})^{2}+(y-y_{M})^{2}\,=\,r^{2}$

mit Mittelpunkt

$M={\begin{pmatrix}x_{M}\\y_{M}\end{pmatrix}}={\begin{pmatrix}0\\0\end{pmatrix}}$ .

Eingesetzt in die Gleichung für den Kreis erhalten wir

$x^{2}+y^{2}=r^{2}\Leftrightarrow y^{2}=r^{2}-x^{2}$ .

Durch Einsetzen in die Formel für Drehkörper um die x-Achse erhält man

${\begin{aligned}V_{\text{Kugel}}&=\pi \int _{-r}^{r}\left(r^{2}-x^{2}\right)\,\mathrm {d} x\\&=\pi \left[r^{2}x-{\frac {1}{3}}x^{3}\right]_{-r}^{r}\\&=\pi \left(r^{3}-{\frac {1}{3}}r^{3}\right)-\pi \left(r^{2}\cdot (-r)-{\frac {1}{3}}(-r)^{3}\right)\\&=\pi \left[\left({\frac {2}{3}}r^{3}\right)-\left(-{\frac {2}{3}}r^{3}\right)\right]\\&={\frac {4}{3}}\pi r^{3}.\\\end{aligned}}$

Oberfläche

Die Kugeloberfläche ist die zweidimensionale Fläche, die den Rand der Kugel bildet. Sie ist also die Menge aller Punkte, deren Abstand zum Kugelmittelpunkt einen festen Wert $\!\ r$ hat. Sie ist eine geschlossene, zweidimensionale Mannigfaltigkeit.

Ihr Flächeninhalt ist ${A}=4\pi {r^{2}}$ und damit gleich groß wie der der Mantelfläche des Kreiszylinders, der die Kugel umhüllt.

Die Kugel besitzt bei gegebenem Volumen die kleinste Oberfläche aller möglichen Körper.

Begründung

Tangente an einer Kugel (Seitenansicht) d = Höhe einer Schicht; r = Radius der Kugel; c = Länge eines Feldes; x = Abstand des Tangentialpunktes von der Mittelachse

Kugelansicht

Teilt man eine Kugel auf in:

Schichten mit einer Höhe von jeweils und
„Meridiane“, die am Äquator ebenfalls den Abstand zueinander haben

und lässt man nach $0$ streben,

so ist die Länge jedes Feldes umgekehrt proportional zu – also zu seinem Abstand von der Mittelachse.

Dies wird aus der oberen Zeichnung rechts deutlich: ist der Abstand des Tangentialpunktes zur Mittelachse. Die Tangente liegt senkrecht zur „Speiche“ und die beiden (rechtwinkligen) Dreiecke sind einander ähnlich. Demnach gilt:

$c={\frac {r}{x}}\ {d}$ .

Die Breite jedes Feldes hingegen ist proportional zu .

Dies ergibt sich direkt aus der unteren Zeichnung, "Ansicht von oben".

Die Länge multipliziert mit der Breite ist demzufolge stets gleich groß, d.h. alle viereckigen Felder haben denselben Flächeninhalt.

Der Flächeninhalt am Äquator beträgt d^2 ( $c\cdot d$ wobei gegen strebt, da ${\frac {r}{x}}$ am Äquator schneller gegen strebt als gegen $0$ ).

Da alle Felder also den Inhalt d^2 haben und es insgesamt (Anzahl der Felder in horizontaler Richtung multipliziert mit der Anzahl der Felder in vertikaler Richtung, also) ${\frac {\text{Umfang}}{d}}\cdot {\frac {\text{Durchmesser}}{d}}={\frac {2\pi r\cdot 2r}{d^{2}}}$ Felder gibt, beträgt der Gesamtflächeninhalt aller Felder: ${A}={4}\pi {r^{2}}$ .

Alternative Herleitung mit Hilfe des Kugelvolumens

Eine Kugel kann man sich aus unendlich vielen, infinitesimalen (unendlich kleinen) Pyramiden zusammengesetzt vorstellen. Die Grundflächen dieser Pyramiden ergeben zusammen die Kugeloberfläche; die Höhen der Pyramiden sind jeweils gleich dem Kugelradius . Da das Pyramiden-Volumen durch die Formel $V_{P}={\tfrac {1}{3}}Gh$ gegeben ist, gilt eine entsprechende Beziehung für das Gesamtvolumen aller Pyramiden, also das Kugelvolumen:

$V={\frac {1}{3}}A_{O}r$ ( $A_{O}$ = Gesamtoberfläche der Kugel)

Wegen $V={\tfrac {4}{3}}\pi r^{3}$ ergibt sich:

${\frac {4}{3}}\pi r^{3}={\frac {1}{3}}A_{O}r$

$A_O = 4 \pi r^2$

Alternative Herleitung mit Hilfe des Kugelvolumens und der Differentialrechnung

Da das Kugelvolumen mit

$V={\frac {4}{3}}\pi r^{3}$

definiert ist und andererseits die Oberfläche eine Veränderung des Volumens laut

$A_{O}={\frac {\mathrm {d} V}{\mathrm {d} r}}=4\pi r^{2}$

ist, ergibt sich die Oberflächenformel sofort aus der Ableitung der Volumenformel.

Herleitung mit Hilfe der Integralrechnung

Aus der ersten Guldin’schen Regel

$A_{O}=2\pi \int \limits _{a}^{b}f(x){\sqrt {1+(f'(x))^{2}}}\,\mathrm {d} x$

für die Mantelfläche eines Rotationskörpers ergibt sich:

${\begin{aligned}A_{O}&=2\pi \int \limits _{-r}^{r}{\sqrt {r^{2}-x^{2}}}{\sqrt {1+\left({\frac {-x}{\sqrt {r^{2}-x^{2}}}}\right)^{2}}}\,\mathrm {d} x\\&=2\pi \int \limits _{-r}^{r}{\sqrt {r^{2}-x^{2}}}{\sqrt {\frac {r^{2}}{r^{2}-x^{2}}}}\,\mathrm {d} x\\&=2\pi \int \limits _{-r}^{r}r\,\mathrm {d} x\\&=2\pi r\int \limits _{-r}^{r}1\,\mathrm {d} x\\&=4\pi r^{2}\end{aligned}}$

Herleitung mit Hilfe der Integralrechnung in Kugelkoordinaten

Für das Flächenelement auf Flächen = konstant gilt in Kugelkoordinaten:

$\mathrm {d} A=r^{2}\sin \theta \,\mathrm {d} \theta \,\mathrm {d} \varphi$ .

Damit lässt sich die Oberfläche einfach berechnen:

${\begin{aligned}A_{O}&=\int \limits _{0}^{2\pi }\int \limits _{0}^{\pi }1\,\mathrm {d} A\\&=\int \limits _{0}^{2\pi }\int \limits _{0}^{\pi }r^{2}\sin \theta \,\mathrm {d} \theta \,\mathrm {d} \varphi \\&=2\pi r^{2}\int \limits _{0}^{\pi }\sin \theta \,\mathrm {d} \theta \\&=4\pi r^{2}\end{aligned}}$

Eigenschaften

Das Verhältnis des Volumens einer Kugel (

) mit Radius zum Volumen des umbeschriebenen Zylinders ( $V_{Z}$ ) ist
$V_{K}:V_{Z}={\frac {4}{3}}\cdot {\frac {1}{2}}\;$ $\Rightarrow V_{K}:V_{Z}=2:3$

Die Kugel besitzt unendlich viele Symmetrieebenen, nämlich die Ebenen durch den Kugelmittelpunkt. Ferner ist die Kugel drehsymmetrisch bezüglich jeder Achse durch den Mittelpunkt und jedes Drehwinkels und punktsymmetrisch bezüglich ihres Mittelpunktes.

Die Kugel besitzt weder Kanten noch Ecken. Ihre Oberfläche lässt sich nicht verzerrungsfrei in der Ebene ausbreiten.
In der Differentialgeometrie hat eine Kugel mit Radius an jedem Punkt der Oberfläche die gaußsche Krümmung $\tfrac{1}{r^2}$ . Auch hieraus folgt, dass die Kugel nicht verzerrungsfrei auf die Ebene (Krümmung 0) abgebildet werden kann.
Die kürzeste Entfernung zwischen zwei Punkten auf der Oberfläche der Kugel (Geodäte) liegt auf einem Großkreis, also einem Kreis durch den Mittelpunkt der Kugel. Geodäten auf der Erdkugel liegen zum Beispiel auf den Längenkreisen, nicht aber auf den Breitenkreisen – mit Ausnahme des Äquators.
Durch die stereografische Projektion kann die Kugel – bis auf den „Nordpol“ – bijektiv auf die Ebene abgebildet werden. Dadurch kann z.B. der Vier-Farben-Satz auf die Kugel übertragen werden. Durch die umgekehrte Abbildung kann die Ebene bijektiv auf die Kugeloberfläche ohne „Nordpol“ abgebildet werden, der „Nordpol“ steht dann für den „unendlich fernen Punkt“. In der Funktionentheorie wird auf diese Art die komplexe Zahlenebene auf die Kugel übertragen (riemannsche Zahlenkugel), sie ist damit eine kompakte riemannsche Fläche vom Geschlecht 0.
Die Kugel hat die kleinste Oberfläche von allen Körpern mit einem vorgegebenen Volumen. Von allen Körpern mit vorgegebener Oberfläche umschließt sie das größte Volumen. Aus diesem Grund tritt die Kugel auch in der Natur auf: Blasen und Wassertropfen sind Kugeln (ohne Berücksichtigung der Gravitation), weil die Oberflächenspannung versucht, die Oberfläche zu minimieren. Planeten sind näherungsweise Kugeln, weil sie bei ihrer Entstehung flüssig waren und die Kugel die Form mit der größten Gravitationsbindungsenergie ist. Die mathematische Kugel ist eine Idealform. In der Natur auftretende Kugeln haben stets nur näherungsweise Kugelform.

Das Verhältnis des Volumens einer Kugel mit Radius zum Volumen des umbeschriebenen Zylinders (Radius , Höhe = , siehe Bild) ist $2:3$ . Das, sowie die Oberflächen- und Volumenformeln waren bereits dem Griechen Archimedes in der Antike bekannt.

Eine Kugel kann auch als Rotationskörper aufgefasst werden: Lässt man eine Halbkreisfläche um ihren Durchmesser rotieren, so entsteht dadurch eine Kugel. Wird der Kreis durch eine Ellipse ersetzt, die um eine ihrer Achsen rotiert, ergibt sich ein Rotationsellipsoid (auch Sphäroid genannt).

Die Kugel rollt auf einer schiefen Ebene selbsttätig abwärts oder sie kann auf einer Fläche durch äußere Krafteinwirkung in allen Richtungen gerollt werden. In der Technik findet man industriell gefertigte (geschliffene) Kugeln schon seit dem 19. Jahrhundert in Rillenkugellagern.

Verallgemeinerung

Höherdimensionale euklidische Räume

Der Begriff der Kugel lässt sich auf Räume anderer Dimension übertragen. Analog zur dreidimensionalen Vollkugel ist für eine natürliche Zahl eine ‑dimensionale Kugel definiert als Menge aller Punkte des ‑dimensionalen euklidischen Raumes, deren Abstand zu einem gegebenen Punkt (dem Mittelpunkt) kleiner gleich einer positiven reellen Zahl (dem Radius) ist. Den Rand der ‑dimensionalen Kugel, also die Menge aller Punkte, deren Abstand vom Mittelpunkt gleich ist, bezeichnet man als ‑dimensionale Sphäre oder kurz ‑Sphäre. Wenn man ohne weitere Angaben von der ‑dimensionalen Kugel spricht, meint man meist die ‑dimensionale Einheitskugel; in diesem Fall liegt der Mittelpunkt im Ursprung des Koordinatensystems und der Radius ist gleich 1.

Nach dieser Definition ist eine dreidimensionale Kugel also eine gewöhnliche Kugel; ihre Oberfläche entspricht einer 2‑Sphäre. Eine zweidimensionale Kugel ist eine Kreisfläche, der zugehörige Kreisrand eine 1‑Sphäre. Eine eindimensionale Kugel schließlich ist eine Strecke, wobei die beiden Streckenendpunkte als 0‑Sphäre aufgefasst werden können.

Hinweis: Diese Begriffe werden nicht einheitlich verwendet. Sphären im Sinne der hier gegebenen Definition werden zuweilen Kugeln genannt. Außerdem sprechen manche Autoren von ‑Sphären, wenn sie (n-1) ‑dimensionale Sphären im ‑dimensionalen Raum meinen.

Das -dimensionale Volumen einer -dimensionalen Kugel mit dem Radius ist

$V_{n}=r^{n}{\frac {\pi ^{n/2}}{\Gamma ({\frac {n}{2}}+1)}}$ .

Hier ist $\Gamma$ die Gammafunktion, eine kontinuierliche Erweiterung der Fakultät. Den (n-1) ‑dimensionalen Inhalt der (n-1) ‑dimensionalen Oberfläche, also der (n-1) ‑Sphäre erhält man durch Ableitung des Volumens nach dem Radius:

$O_{n}=nr^{n-1}{\frac {\pi ^{n/2}}{\Gamma ({\frac {n}{2}}+1)}}=2r^{n-1}{\frac {\pi ^{n/2}}{\Gamma ({\frac {n}{2}})}}$ .

Volumen und Oberflächen von Einheitskugeln in Dimensionen

Für eine Einheitskugel in Dimensionen findet man also folgende Volumen und Oberflächeninhalte:

Dimensionen	1	2	3	4	5	6	7	8	9	10	…	2n	2n+1
Volumen	2	$\pi$	${\frac {4\pi }{3}}$	${\frac {\pi ^{2}}{2}}$	${\frac {8\pi ^{2}}{15}}$	${\frac {\pi ^{3}}{6}}$	${\frac {16\pi ^{3}}{105}}$	${\frac {\pi ^{4}}{24}}$	${\frac {32\pi ^{4}}{945}}$	${\frac {\pi ^{5}}{120}}$	…	${\frac {\pi ^{n}}{n!}}$	${\frac {2^{n+1}\pi ^{n}}{1\cdot 3\cdot \ldots \cdot (2n+1)}}$
Oberfläche	2	$2\pi$	$4\pi$	$2\pi ^{2}$	${\frac {8\pi ^{2}}{3}}$	$\pi ^{3}$	${\frac {16\pi ^{3}}{15}}$	${\frac {\pi ^{4}}{3}}$	${\frac {32\pi ^{4}}{105}}$	${\frac {\pi ^{5}}{12}}$	…	${\frac {2\pi ^{n}}{(n-1)!}}$	${\frac {2^{n+1}\pi ^{n}}{1\cdot 3\cdot \ldots \cdot (2n-1)}}$

Eine -Sphäre ist ein Beispiel einer kompakten -Mannigfaltigkeit.

Metrische Räume

Den Begriff der Kugel kann man auf alle Räume verallgemeinern, in denen man einen Abstandsbegriff hat, das sind die metrischen Räume.

Ist (X,d) ein metrischer Raum, $a\in X$ und $r\in \mathbb {R}$ , r>0 , so nennt man

$B(a,r)=\{x\in X\mid d(a,x)<r\}$

die offene Kugel mit Mittelpunkt und Radius . Die Menge:

${\overline {B}}(a,r)=\{x\in X\mid d(a,x)\leq r\}$

heißt abgeschlossene Kugel.

Manche Autoren schreiben auch U(a,r) für die offenen und B(a,r) für die abgeschlossenen Kugeln. Andere Schreibweisen für die offenen Kugeln sind $B_{r}(a)$ und $U_{r}(a)$ .

Dichteste Kugelpackung

→ Hauptartikel: Dichteste Kugelpackung

Dichteste Kugelpackung
grau: unterste Schicht (A-Schicht)
gelb und rot: B-Schicht oder C-Schicht (hier als zweite Schicht; allgemein in beliebiger Reihenfolge als zweite oder dritte Schicht)

Die dichteste Kugelpackung ist diejenige gegenseitige Anordnung gleich großer Kugeln, die den kleinsten Raum beansprucht. Der leere Raum zwischen den dichtest gepackten Kugeln nimmt nur etwa 26 % des Gesamtraumes ein, bzw. die Packungsdichte beträgt etwa 74 %:

${\frac {\pi }{3{\sqrt {2}}}}\approx 0{,}74048\approx 74\,\%$ .

Diese Anordnung kann auf zweierlei Art beschrieben werden:
Sie besteht aus ebenen Schichten aus sich berührenden Kugeln,

von denen jede von sechs benachbarten Kugeln und von je drei Kugeln aus der Schicht darüber und aus der darunter berührt wird, oder
von denen jede von vier benachbarten Kugeln und von je vier Kugeln aus der Schicht darüber und aus der darunter berührt wird.

Die erste der beiden Beschreibungen ist die bevorzugt gebrauchte. Die darin enthaltene Schicht wird als hexagonale (regelmäßig sechseckige) Kugel-Schicht, die im zweiten Fall als tetragonale (quadratische) Kugel-Schicht bezeichnet.

Symbolik

Die Kugelform gilt seit altersher als „vollkommene Form“. Erst seit dem Aufkommen der Drechseltechniken war sie – zumindest aus Holz oder weichem Stein – nahezu perfekt herzustellen. Später wurde sie zu einem Sinnbild der Unendlichkeit (manchmal auch des Kosmos). Mit dem Aufkommen von Feuerwaffen wurden Kanonen- und Gewehrkugeln immer mehr auch zu einem Inbegriff von Stärke und Macht.

Anwendungsbeispiele

Erde, Mond und Mars

Die Erde, der Mond und der Mars haben annähernd die Form einer Kugel.

Erde

Die Erde hat den mittleren Durchmesser 12742 km, also den mittleren Radius $r=6371\ \mathrm {km}$ . Die Masse der Erde beträgt etwa 5,9724 · 10²⁴ kg. Daraus ergibt sich mithilfe der oben genannten Formeln für das Volumen, die mittlere Dichte und die Oberfläche:

Volumen: $V={\frac {4}{3}}\cdot \pi \cdot r^{3}={\frac {4}{3}}\cdot \pi \cdot (6371\ \mathrm {km} )^{3}\approx 1{,}0832\cdot 10^{12}\ \mathrm {km^{3}}$

Mittlere Dichte: $\rho ={\frac {m}{V}}={\frac {5{,}9724\cdot 10^{24}\ \mathrm {kg} }{1{,}0832\cdot 10^{12}\ \mathrm {km^{3}} }}={\frac {5{,}9724\cdot 10^{24}\ \mathrm {kg} }{1{,}0832\cdot 10^{21}\ \mathrm {m^{3}} }}\approx 5514\ \mathrm {kg} /\mathrm {m^{3}}$

Die Erde hat also im Durchschnitt eine etwa fünfeinhalb Mal so hohe Dichte wie Wasser unter Standardbedingungen.

Oberfläche: $A=4\cdot \pi \cdot r^{2}=4\cdot \pi \cdot (6371\ \mathrm {km} )^{2}\approx 5{,}101\cdot 10^{8}\ \mathrm {km^{2}}$

Mond

Der Mond hat den mittleren Durchmesser 3474 km, also den mittleren Radius $r=1737\ \mathrm {km}$ . Die Masse des Mondes beträgt etwa 7,346 · 10²² kg. Daraus ergibt sich:

Volumen: $V={\frac {4}{3}}\cdot \pi \cdot r^{3}={\frac {4}{3}}\cdot \pi \cdot (1737\ \mathrm {km} )^{3}\approx 2{,}1958\cdot 10^{10}\ \mathrm {km^{3}}$

Das ist etwa 2,0 Prozent des Volumens der Erde.

Mittlere Dichte: $\rho ={\frac {m}{V}}={\frac {7{,}346\cdot 10^{22}\ \mathrm {kg} }{2{,}1958\cdot 10^{10}\ \mathrm {km^{3}} }}={\frac {7{,}346\cdot 10^{22}\ \mathrm {kg} }{2{,}1958\cdot 10^{19}\ \mathrm {m^{3}} }}\approx 3345\ \mathrm {kg} /\mathrm {m^{3}}$

Der Mond hat also im Durchschnitt eine gut 3,3 Mal so hohe Dichte wie Wasser unter Standardbedingungen.

Oberfläche: $A=4\cdot \pi \cdot r^{2}=4\cdot \pi \cdot (1737\ \mathrm {km} )^{2}\approx 3{,}793\cdot 10^{7}\ \mathrm {km^{2}}$

Das ist etwa 7,4 Prozent der Oberfläche der Erde.

Mars

Der Mars hat den mittleren Durchmesser 6780 km, also den mittleren Radius $r=3390\ \mathrm {km}$ . Die Masse des Mars beträgt etwa 6,417 · 10²³ kg. Daraus ergibt sich:

Volumen: $V={\frac {4}{3}}\cdot \pi \cdot r^{3}={\frac {4}{3}}\cdot \pi \cdot (3390\ \mathrm {km} )^{3}\approx 1{,}6318\cdot 10^{11}\ \mathrm {km^{3}}$

Das ist etwa 15,1 Prozent des Volumens der Erde.

Mittlere Dichte: $\rho ={\frac {m}{V}}={\frac {6{,}417\cdot 10^{23}\ \mathrm {kg} }{1{,}6318\cdot 10^{11}\ \mathrm {km^{3}} }}={\frac {6{,}417\cdot 10^{23}\ \mathrm {kg} }{1{,}6318\cdot 10^{20}\ \mathrm {m^{3}} }}\approx 3933\ \mathrm {kg} /\mathrm {m^{3}}$

Der Mars hat also im Durchschnitt eine knapp vier Mal so hohe Dichte wie Wasser unter Standardbedingungen.

Oberfläche: $A=4\cdot \pi \cdot r^{2}=4\cdot \pi \cdot (3390\ \mathrm {km} )^{2}\approx 1{,}448\cdot 10^{8}\ \mathrm {km^{2}}$

Das ist etwa 28,4 Prozent der Oberfläche der Erde.

Siehe auch

Großkreis
Sphäre
Sphärische Geometrie • Sphärische Trigonometrie
Kugelzweieck • Kugeldreieck
Kugelsegment
Einheitskugel

Basierend auf einem Artikel in:

Wikipedia.de