
Parallelität (Geometrie)
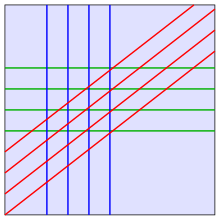
In der euklidischen Geometrie definiert man: Zwei Geraden sind parallel, wenn sie in einer Ebene liegen und einander nicht schneiden. Außerdem setzt man fest, dass jede Gerade zu sich selbst parallel sein soll. Zwei Geraden werden als echt parallel bezeichnet, wenn sie parallel, aber nicht identisch sind.
Häufig wird von echt parallelen Geraden gesagt, dass sie einander „im Unendlichen“ schneiden. Diese Aussage bekommt einen präzisen Sinn, wenn der euklidische Raum zu einem projektiven Raum erweitert wird.
Im dreidimensionalen euklidischen Raum gilt ferner:
- Zwei Geraden, die nicht in einer Ebene liegen, werden windschief genannt. (Auch sie haben keinen Schnittpunkt, sind aber nicht parallel.)
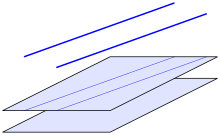
- Eine Gerade ist parallel zu einer Ebene, wenn sie ganz in dieser Ebene liegt oder diese nicht schneidet.
- Zwei Ebenen sind parallel, wenn sie zusammenfallen oder einander nicht schneiden. Man spricht von Parallelebenen.
Analoge Sprechweisen gelten für euklidische und affine Geometrien in beliebiger Dimension und für die analytische Geometrie (die Geometrie in euklidischen Vektorräumen). Insbesondere sind zwei Geraden in einem Vektorraum parallel, wenn ihre Richtungsvektoren linear abhängig (oder proportional) sind.
Eigenschaften
In der ebenen euklidischen und affinen Geometrie gilt:
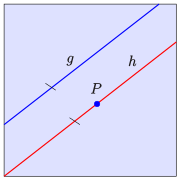
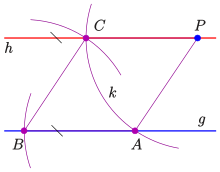
- Zu jeder Geraden und jedem Punkt, der nicht auf der Geraden liegt, gibt es genau eine Gerade, die zur gegebenen Geraden parallel ist und durch den gegebenen Punkt geht (die Parallele durch diesen Punkt).
Diese Aussage wird das Parallelenaxiom genannt, da sie bei einem axiomatischen Aufbau der euklidischen Geometrie als Axiom benötigt wird. In der analytischen Geometrie (Geometrie in euklidischen Vektorräumen) ist sie hingegen beweisbar (also ein Satz). In affinen Räumen beliebiger Dimension gilt:
- Die Beziehung „parallel“ zwischen Geraden bildet eine Äquivalenzrelation, die Geraden lassen sich also aufteilen in Äquivalenzklassen zueinander paralleler Geraden. Eine solche Äquivalenzklasse wird als Parallelenschar bezeichnet und bildet ein spezielles Büschel.
- Fügt man einem affinen Raum für jede Parallelenschar einen "unendlich fernen" (auch "uneigentlichen") Punkt (Fernpunkt) hinzu, in dem sich dann je zwei Geraden der Schar schneiden, erhält man einen projektiven Raum als projektiven Abschluss des affinen Raumes.
In der euklidischen Geometrie gilt ferner bei beliebiger Dimension des Raumes:
- Bei parallelen Geraden
und
ist der Abstand aller Punkte von
zur Geraden
konstant (und umgekehrt), die Geraden sind also immer gleich weit voneinander entfernt. Entsprechendes gilt für parallele Ebenen.
Außerhalb der euklidischen Geometrie gilt: Ersetzt man das Parallelenaxiom durch die Forderung Zu jeder Geraden und jedem Punkt, der nicht auf der Geraden liegt, gibt es mindestens zwei Geraden durch den Punkt, welche die gegebene Gerade nicht schneiden, so erhält man eine nichteuklidische Geometrie, nämlich die hyperbolische.
Verallgemeinerung für affine Räume
In einem -dimensionalen
affinen Raum
über einem Körper
können affine Teilräume
als Nebenklassen
von linearen
Teilräumen
des zu
gehörenden Koordinatenvektorraums beschrieben werden. Dann ist
und
.
Man definiert nun:
- Die Räume
und
sind parallel, wenn
oder
gilt.
Allein mit geometrischen Begriffen kann Parallelität gleichwertig so definiert werden:
- Die Räume
und
sind parallel, wenn es eine Parallelverschiebung
des affinen Raumes
gibt, so dass
oder
gilt.
Vektoriell geschrieben entspricht
einem Verschiebungsvektor
(es kann zum Beispiel
aus der ersten Darstellung gewählt werden) und die Aussage lautet dann
- Die Räume
und
sind parallel, wenn es eine Verschiebung
gibt, so dass
oder
gilt.
Meistens wird diese sehr allgemeine Definition auf affine Teilräume beschränkt, die mindestens eindimensional sind, da sonst im Sinne der Definition die leere Menge und einpunktige Mengen zu jedem beliebigen Teilraum parallel wären.
Eigenschaften
- Die verallgemeinerte Parallelität ist auf der Menge der
-dimensionalen Teilräume eines
-dimensionalen affinen Raumes (für festes
) eine Äquivalenzrelation. Eine Äquivalenzklasse wird als Parallelenschar von Ebenen, speziell für
als Parallelenschar von Hyperebenen bezeichnet.
- In der Sprache der projektiven Geometrie besteht eine solche
Parallelenschar von
-dimensionalen Ebenen aus allen Ebenen, die sich in einem
-dimensionalen (projektiven) Teilraum der Fernhyperebene schneiden. Daher spricht man auch von einem Ebenenbüschel. (Zu den Begriffen Bündel und Büschel in der projektiven Geometrie siehe Projektiver Raum#Projektiver Teilraum.)
- Auf der Menge aller affinen Teilräume (beliebiger Dimension
) ist die Parallelität zwar symmetrisch und reflexiv, aber für
nicht transitiv, also im Allgemeinen keine Äquivalenzrelation.
Verwandte Begriffe
.png)
Die Idee des parallelen Verlaufs wird auch in anderen Situationen verwendet, wobei meist die Charakterisierung durch den konstanten Abstand übertragen wird.
- Bei einer Parallelverschiebung wird jeder Punkt um einen „konstanten Betrag in dieselbe Richtung“ verschoben
- (in Vektorräumen:
).
- Somit können auch Strecken und Halbgeraden parallel zueinander verlaufen, obwohl diese Sonderfälle durch die euklidische Definition nicht erfasst sind.
- Eine Parallelkurve zu einer ebenen Kurve erhält man, indem man in jedem Punkt der Kurve einen konstanten Betrag in Richtung der Normalen in diesem Punkt aufträgt.
- (für eine Kurve
sind das die Kurven
, wenn
der normierte Normalvektor zu
ist).
- (Beispiel: konzentrische Kreise)
- Einen Parallelkörper zu einem (abgeschlossenen) konvexen Körper erhält man, wenn man den Körper "um r vergrößert", d.h., alle Punkte hinzufügt, deren Abstand kleiner oder gleich r ist, indem man die Vereinigung aller Kugeln mit Radius r bildet, deren Mittelpunkt in dem Körper liegt.
- (In Vektorräumen:
, wobei
die Kugel mit Radius r um den Ursprung ist.)
- Zwei Vektoren, welche genau in zueinander entgegengesetzte Richtung zeigen, sind antiparallel.
- In Laguerre-Ebenen und Minkowski-Ebenen gibt es parallele Punkte. Das sind Punkte, die nicht durch einen Zykel (Parabel bzw. Hyperbel) verbunden werden können.
Verallgemeinerungen für endliche Geometrien
In der endlichen Geometrie wird das Konzept der Parallelität (als Äquivalenzrelation) in allgemeinerer Form auch für Blockpläne definiert. Endliche affine und projektive Geometrien können als spezielle Blockpläne aufgefasst werden. Die Einteilung der „Geraden“, die in der endlichen Geometrie auch als „Blöcke“ bezeichnet werden, in „Parallelenscharen“ wird in der Theorie der Blockpläne zum Konzept der Auflösung eines Blockplans verallgemeinert. Eine weitere Verallgemeinerung der Auflösung ist das Konzept der taktischen Zerlegung.
Siehe auch
Andere Lagebeziehungen von Geraden sind:


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 23.10. 2022