
Untervektorraum

Ein Untervektorraum, Teilvektorraum, linearer Unterraum oder linearer Teilraum ist in der Mathematik eine Teilmenge eines Vektorraums, die selbst wieder einen Vektorraum darstellt. Dabei werden die Vektorraumoperationen Vektoraddition und Skalarmultiplikation von dem Ausgangsraum auf den Untervektorraum vererbt. Jeder Vektorraum enthält sich selbst und den Nullvektorraum als triviale Untervektorräume.
Jeder Untervektorraum ist das Erzeugnis einer linear unabhängigen Teilmenge von Vektoren des Ausgangsraums. Die Summe und der Durchschnitt zweier Untervektorräume ergibt wieder einen Untervektorraum, dessen Dimension über die Dimensionsformel ermittelt werden kann. Jeder Untervektorraum besitzt mindestens einen Komplementärraum, sodass der Ausgangsraum die direkte Summe aus dem Untervektorraum und seinem Komplement ist. Weiter kann jedem Untervektorraum ein Faktorraum zugeordnet werden, der dadurch entsteht, dass alle Elemente des Ausgangsraums entlang des Untervektorraums parallelprojiziert werden.
Untervektorräume werden in der linearen Algebra unter anderem dazu verwendet, Kern und Bild von linearen Abbildungen, Lösungsmengen von linearen Gleichungen und Eigenräume von Eigenwertproblemen zu charakterisieren. In der Funktionalanalysis werden insbesondere Untervektorräume von Hilberträumen, Banachräumen und Dualräumen untersucht. Untervektorräume besitzen vielfältige Anwendungen, beispielsweise bei numerischen Lösungsverfahren für große lineare Gleichungssysteme und für partielle Differentialgleichungen, bei Optimierungsproblemen, in der Kodierungstheorie und in der Signalverarbeitung.
Definition
Ist
ein Vektorraum über einem Körper
,
so bildet eine Teilmenge
genau dann einen Untervektorraum von
,
wenn sie nichtleer und abgeschlossen
bezüglich der Vektoraddition
und der Skalarmultiplikation
ist. Es muss also
für alle Vektoren
und alle Skalare
gelten. Dabei sind die Vektoraddition und die Skalarmultiplikation im
Untervektorraum
die Einschränkungen
der entsprechenden Operationen des Ausgangsraums
.
Äquivalent zur ersten Bedingung kann man auch fordern, dass der Nullvektor von
in
enthalten ist. Enthält nämlich
zumindest ein Element, dann ist aufgrund der Abgeschlossenheit von
bezüglich der Skalarmultiplikation auch der Nullvektor in
enthalten (setze
).
Umgekehrt ist die Menge
,
wenn sie den Nullvektor enthält, nichtleer.
Mit Hilfe dieser drei Kriterien lässt sich überprüfen, ob eine gegebene
Teilmenge
eines Vektorraums
ebenfalls einen Vektorraum bildet, ohne alle Vektorraumaxiome
nachweisen zu müssen. Ein Untervektorraum wird häufig kurz als „Unterraum“
bezeichnet, wenn aus dem Kontext klar ist, dass es sich dabei um einen linearen Unterraum und
nicht um einen allgemeineren Unterraum
handelt.
Beispiele
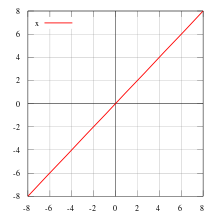
Konkrete Beispiele
Die Menge aller Vektoren
der reellen Zahlenebene
bildet mit der üblichen komponentenweisen Vektoraddition und
Skalarmultiplikation einen Vektorraum. Die Teilmenge
der Vektoren, für die
gilt, bildet einen Untervektorraum von
,
denn es gilt für alle
:
- der Koordinatenursprung
liegt in
Als weiteres Beispiel kann man den Vektorraum
aller reellen Funktionen
mit der üblichen punktweisen Addition und Skalarmultiplikation betrachten. In
diesem Vektorraum bildet die Menge
der linearen
Funktionen
einen Untervektorraum, denn es gilt für
:
- die Nullfunktion
liegt in
, somit
, somit
Allgemeinere Beispiele
- Jeder Vektorraum enthält sich selbst und den Nullvektorraum
, der nur aus dem Nullvektor besteht, als triviale Untervektorräume.
- Im
-Vektorraum der reellen Zahlen sind die Menge
und ganz
die einzigen Untervektorräume.
- Im
-Vektorraum der komplexen Zahlen
sind die Menge der reellen Zahlen
und die Menge der imaginären Zahlen
Untervektorräume.
- In der euklidischen
Ebene
bilden alle Geraden durch den Nullpunkt Untervektorräume.
- Im euklidischen
Raum
bilden alle Ursprungsgeraden und Ursprungsebenen Untervektorräume.
- Im Vektorraum aller Polynome
bildet die Menge der Polynome vom Maximalgrad
für jede natürliche Zahl
einen Untervektorraum.
- Im Vektorraum der quadratischen Matrizen bilden die symmetrischen und die schiefsymmetrischen Matrizen jeweils Untervektorräume.
- Im Vektorraum der reellen Funktionen über einem Intervall bilden die integrierbaren Funktionen, die stetigen Funktionen und die differenzierbaren Funktionen jeweils Untervektorräume.
- Im Vektorraum aller Abbildungen zwischen zwei Vektorräumen über demselben Körper bildet die Menge der linearen Abbildungen einen Untervektorraum.
Eigenschaften
Vektorraumaxiome
Die drei Unterraumkriterien sind tatsächlich hinreichend
und notwendig für die Gültigkeit aller Vektorraumaxiome. Aufgrund der
Abgeschlossenheit der Menge
gilt nämlich für alle Vektoren
durch Setzen von
und damit weiter durch Setzen von
.
Damit enthält die Menge
insbesondere den Nullvektor und zu jedem Element
auch das additiv inverse
Element
.
Also ist
eine Untergruppe von
und damit insbesondere eine abelsche
Gruppe. Das Assoziativgesetz,
das Kommutativgesetz,
die Distributivgesetze
und die Neutralität
der Eins übertragen sich direkt von dem Ausgangsraum
auf
.
Damit erfüllt
alle Vektorraum-Axiome und ist ebenfalls ein Vektorraum. Umgekehrt muss jeder
Untervektorraum
die drei angegebenen Kriterien erfüllen, da die Vektoraddition und die
Skalarmultiplikation die Einschränkungen der entsprechenden Operationen von
sind.
Darstellung

Jede Teilmenge
von Vektoren eines Vektorraums
spannt durch Bildung aller möglichen Linearkombinationen
,
einen Untervektorraum von
auf, den man die lineare
Hülle von
nennt. Die lineare Hülle ist der kleinste Untervektorraum, der die Menge
umfasst und gleich dem Durchschnitt aller Untervektorräume von
,
die
umfassen. Umgekehrt ist jeder Untervektorraum
das Erzeugnis
einer Teilmenge
von
,
das heißt, es gilt
,
wobei man die Menge
ein Erzeugendensystem
von
nennt. Ein minimales Erzeugendensystem besteht aus linear
unabhängigen Vektoren und heißt Basis
eines Vektorraums. Die Anzahl
der Elemente einer Basis gibt die Dimension
eines Vektorraums an.
Operationen
Durchschnitt und Vereinigung
Der Durchschnitt
zweier Untervektorräume
eines Vektorraums
ist stets selbst ein Untervektorraum.
Die Vereinigung zweier Untervektorräume
ist jedoch nur dann ein Untervektorraum, wenn
oder
gilt. Anderenfalls ist die Vereinigung zwar abgeschlossen bezüglich der
Skalarmultiplikation, aber nicht bezüglich der Vektoraddition.
Summe
Die Summe zweier Untervektorräume
eines Vektorraums
ist wieder ein Untervektorraum, und zwar der kleinste Untervektorraum, der
enthält. Für die Summe zweier endlichdimensionaler Untervektorräume gilt die
Dimensionsformel
,
woraus sich umgekehrt auch die Dimension des Durchschnitts zweier Untervektorräume ablesen lässt. Schnitt- und Summenbasen von Untervektorräumen endlicher Dimension lassen sich mit dem Zassenhaus-Algorithmus berechnen.
Direkte Summe
Besteht der Schnitt zweier Untervektorräume
lediglich aus dem Nullvektor, ist also
,
so bezeichnet man die Summe als innere direkte
Summe
,
denn sie ist isomorph
zur äußeren
direkten Summe der beiden Vektorräume. In diesem Fall gibt es zu jedem
eindeutig bestimmte Vektoren
,
mit
.
Aus dem Dimensionssatz folgt dann, da der Nullvektorraum nulldimensional ist,
für die Dimension der direkten Summe
,
was auch im unendlichdimensionalen Fall wahr ist.
Mehrere Operanden
Die vorangegangenen Operationen lassen sich auch auf mehr als zwei Operanden
verallgemeinern. Ist
eine Familie
von Untervektorräumen von
,
wobei
eine beliebige Indexmenge
ist, dann bildet der Durchschnitt dieser Untervektorräume
wiederum einen Untervektorraum von .
Weiter ergibt auch die Summe mehrerer Untervektorräume
wieder einen Untervektorraum von ,
wobei im Fall einer Indexmenge mit unendlich vielen Elementen nur endlich viele
Summanden ungleich dem Nullvektor sein dürfen. Eine solche Summe heißt direkt
und wird dann mit
bezeichnet, wenn der Schnitt jedes Untervektorraums
mit der Summe der übrigen Untervektorräume den Nullvektorraum ergibt. Das ist
äquivalent dazu, dass jeder Vektor eine eindeutige Darstellung als Summe von
Elementen der Untervektorräume besitzt.
Abgeleitete Räume
Komplementärraum
Zu jedem Untervektorraum
von
existiert mindestens ein Komplementärraum
,
sodass
gilt. Jedem solchen Komplementärraum entspricht genau eine Projektion
auf den Untervektorraum
,
also eine idempotente
lineare Abbildung
,
mit der
gilt, wobei
die identische
Abbildung ist. Im Allgemeinen existieren mehrere Komplementärräume zu einem
Untervektorraum, von denen durch die Vektorraumstruktur keiner ausgezeichnet
ist. In Skalarprodukträumen
ist es allerdings möglich, von zueinander orthogonalen
Untervektorräumen zu sprechen. Ist
endlichdimensional, dann existiert zu jedem Untervektorraum
ein eindeutig bestimmter orthogonaler Komplementärraum, der gerade das orthogonale
Komplement
von
ist, und es gilt dann
.
Faktorraum
Jedem Untervektorraum
eines Vektorraums
kann ein Faktorraum
zugeordnet werden, der dadurch entsteht, dass alle Elemente des Untervektorraums
miteinander identifiziert werden und so die Elemente des Vektorraums entlang des
Untervektorraums parallelprojiziert
werden. Formal ist der Faktorraum definiert als Menge der Äquivalenzklassen
von Vektoren in ,
wobei die Äquivalenzklasse eines Vektors
die Menge der Vektoren in
ist, die sich von
nur um ein Element
des Untervektorraums
unterscheiden. Der Faktorraum bildet einen Vektorraum, wenn die
Vektorraumoperationen vertreterweise definiert werden, er ist aber selbst kein
Untervektorraum von
.
Für die Dimension des Faktorraums gilt
.
Die Untervektorräume von
sind genau die Faktorräume
,
wobei
Untervektorraum von
mit
ist.
Annihilatorraum
Der Dualraum
eines Vektorraums
über einem Körper
ist der Raum der linearen Abbildungen von
nach
und damit selbst ein Vektorraum. Für eine Teilmenge
von
bildet die Menge aller Funktionale, die auf
verschwinden, einen Untervektorraum des Dualraums, den sogenannten
Annihilatorraum
.
Ist
endlichdimensional, so gilt für die Dimension des Annihilatorraums eines
Untervektorraums
von
.
Der Dualraum
eines Untervektorraums
ist damit isomorph zum Faktorraum
.
Untervektorräume in der linearen Algebra
Lineare Abbildungen
Ist
eine lineare Abbildung zwischen zwei Vektorräumen
und
über dem gleichen Körper, dann bildet der Kern
der Abbildung
einen Untervektorraum von
und das Bild
der Abbildung
einen Untervektorraum von .
Weiterhin ist der Graph
einer linearen Abbildung ein Untervektorraum des Produktraums
.
Ist der Vektorraum
endlichdimensional, so gilt für die Dimensionen der involvierten Räume der Rangsatz
.
Die Dimension des Bilds nennt man auch Rang
und die Dimension des Kerns auch Defekt
der linearen Abbildung. Nach dem Homomorphiesatz
ist dabei das Bild isomorph
zum Faktorraum .
Lineare Gleichungen
Ist
wiederum eine lineare Abbildung zwischen zwei Vektorräumen über dem gleichen
Körper, dann ist die Lösungsmenge
der homogenen
linearen Gleichung
ein Untervektorraum von ,
und zwar gerade der Kern von
.
Die Lösungsmenge einer inhomogenen linearen Gleichung
mit
ist hingegen, sofern sie nichtleer ist, ein affin-linearer
Unterraum von
,
was eine Folge der Superpositionseigenschaft
ist. Die Dimension des Lösungsraums ist dann ebenfalls gleich der Dimension des
Kerns von
.
Eigenwertprobleme
Ist nun
eine lineare Abbildung eines Vektorraums in sich, also ein Endomorphismus, mit
zugehörigem Eigenwertproblem
,
dann ist jeder zu einem Eigenwert
zugehörige Eigenraum
ein Untervektorraum von ,
dessen vom Nullvektor verschiedene Elemente genau die zugehörigen Eigenvektoren
sind. Die Dimension des Eigenraums entspricht der geometrischen
Vielfachheit des Eigenwerts; sie ist maximal so groß wie die algebraische
Vielfachheit des Eigenwerts.
Invariante Untervektorräume
Ist wieder
ein Endomorphismus, dann heißt ein Untervektorraum
von
invariant unter
oder kurz
-invariant,
falls
gilt, das heißt, wenn für alle
das Bild
ebenfalls in
liegt. Das Bild von
unter
ist dann also ein Untervektorraum von
.
Die trivialen Untervektorräume
und
,
aber auch
,
und alle Eigenräume von
sind stets invariant unter
.
Ein weiteres wichtiges Beispiel für invariante Untervektorräume sind die Haupträume,
die beispielsweise bei der Bestimmung der jordanschen
Normalform verwendet werden.
Untervektorräume in der Funktionalanalysis
Unterhilberträume
In Hilberträumen, also vollständigen Skalarprodukträumen, werden insbesondere Unterhilberträume betrachtet, das heißt Untervektorräume, die bezüglich der Einschränkung des Skalarprodukts immer noch vollständig sind. Diese Eigenschaft ist gleichbedeutend damit, dass der Untervektorraum abgeschlossen bezüglich der Normtopologie, die durch das Skalarprodukt induziert wird, ist. Nicht jeder Untervektorraum eines Hilbertraums ist auch vollständig, es lässt sich jedoch zu jedem unvollständigen Untervektorraum durch Abschlussbildung ein Unterhilbertraum erhalten, in dem jener dann dicht liegt. Zu jedem Unterhilbertraum existiert nach dem Projektionssatz auch ein eindeutig bestimmtes orthogonales Komplement, das stets abgeschlossen ist.
Unterhilberträume spielen eine wichtige Rolle in der Quantenmechanik und der Fourier- oder Multiskalenanalyse von Signalen.
Unterbanachräume
In Banachräumen, also vollständigen normierten Räumen, kann man analog dazu Unterbanachräume, das heißt Untervektorräume, die bezüglich der Einschränkung der Norm vollständig sind, betrachten. Wie im Hilbertraumfall ist ein Untervektorraum eines Banachraums genau dann ein Unterbanachraum, wenn er abgeschlossen ist. Weiter lässt sich zu jedem unvollständigen Untervektorraum eines Banachraums durch Vervollständigung ein Unterbanachraum erhalten, der dicht in diesem liegt. Zu einem Unterbanachraum existiert jedoch im Allgemeinen kein komplementärer Unterbanachraum.
In einem halbnormierten Raum bilden die Vektoren mit Halbnorm Null einen Untervektorraum. Aus einem halbnormierten Raum erhält man einen normierten Raum als Faktorraum, indem man Äquivalenzklassen von Vektoren, die sich bezüglich der Halbnorm nicht unterscheiden, betrachtet. Ist der halbnormierte Raum vollständig, so ist dieser Faktorraum dann ein Banachraum. Diese Konstruktion wird insbesondere bei den Lp-Räumen und verwandten Funktionenräumen eingesetzt.
Bei der numerischen Berechnung partieller Differentialgleichungen mittels der Finite-Elemente-Methode wird die Lösung in geeigneten endlichdimensionalen Unterbanachräumen des zugrundeliegenden Sobolevraums approximiert.
Topologische Dualräume
In der Funktionalanalysis betrachtet man neben dem algebraischen Dualraum
auch den topologischen Dualraum
eines Vektorraums
,
der aus den stetigen
linearen Abbildungen von
nach
besteht. Für einen topologischen
Vektorraum bildet der topologische Dualraum einen Untervektorraum des
algebraischen Dualraums. Nach dem Satz
von Hahn-Banach besitzt ein lineares
Funktional auf einem Untervektorraum eines reellen oder komplexen
Vektorraums, das von einer sublinearen
Funktion beschränkt wird, eine lineare Fortsetzung
auf dem Gesamtraum, die ebenfalls durch diese sublineare Funktion beschränkt
wird. Als Konsequenz enthält der topologische Dualraum eines normierten Raums
ausreichend viele Funktionale, was die Grundlage einer reichhaltigen
Dualitätstheorie bildet.
Weitere Anwendungen
Weitere wichtige Anwendungen von Untervektorräumen sind:
- Das Gram-Schmidtsche Orthogonalisierungsverfahren zur Konstruktion von Orthogonalbasen
- Krylow-Unterraum-Verfahren zur Lösung großer dünnbesetzter linearer Gleichungssysteme
- Lösungsverfahren für Optimierungsprobleme
- Lineare Codes in der Kodierungstheorie
- Die Darstellung projektiver Räume in der projektiven Geometrie
Siehe auch
Literatur
- Siegfried Bosch: Lineare Algebra. Springer, 2006, ISBN 3-540-29884-3.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 23.12. 2025