Banachraum
Ein Banachraum (auch Banach-Raum, Banachscher Raum) ist in der Mathematik ein vollständiger normierter Vektorraum. Banachräume gehören zu den zentralen Studienobjekten der Funktionalanalysis. Insbesondere sind viele unendlichdimensionale Funktionenräume Banachräume. Sie sind nach dem Mathematiker Stefan Banach benannt, der sie 1920–1922 gemeinsam mit Hans Hahn und Eduard Helly vorstellte.
Definition
Ein Banachraum ist ein vollständiger normierter Raum
,
das heißt ein Vektorraum
über dem Körper
der reellen oder komplexen Zahlen mit
einer Norm
,
in dem jede Cauchy-Folge
aus Elementen von
in der von der Norm induzierten Metrik
konvergiert.
Erläuterungen
Bei metrischen Räumen ist die Vollständigkeit eine Eigenschaft der Metrik, nicht des topologischen Raums selbst. Geht man zu einer äquivalenten Metrik über (das heißt zu einer Metrik, die dieselbe Topologie erzeugt), dann kann die Vollständigkeit verloren gehen. Für zwei äquivalente Normen auf einem normierten Raum hingegen gilt, dass die eine genau dann vollständig ist, wenn die andere es ist. Im Falle der normierten Räume ist die Vollständigkeit daher eine Eigenschaft der Normtopologie, die nicht von der konkreten Norm abhängt.
Sätze und Eigenschaften
- Ein normierter Raum ist genau dann ein Banachraum, wenn in ihm jede absolut konvergente Reihe konvergiert.
- Jeder normierte Raum lässt sich vervollständigen, wodurch man einen Banachraum erhält, der den ursprünglichen Raum als dichten Teilraum enthält.
- Ist eine lineare
Abbildung
zwischen zwei normierten Räumen ein Isomorphismus, dann folgt aus der Vollständigkeit von
die Vollständigkeit von
.
- Jeder endlichdimensionale normierte Raum ist ein Banachraum. Umgekehrt ist ein Banachraum, der eine höchstens abzählbare Hamelbasis besitzt, endlichdimensional. Letzteres ist eine Konsequenz aus der Baireschen Eigenschaft vollständiger metrischer Räume.
- Ist
ein abgeschlossener Untervektorraum eines Banachraums
, dann ist
wieder ein Banachraum. Auch der Faktorraum
mit der Norm
ist dann ein Banachraum.
- Der erste Isomorphiesatz für Banachräume: Ist das Bild einer beschränkten
linearen Abbildung
zwischen zwei Banachräumen abgeschlossen, dann ist
. Hierbei handelt es sich um den Begriff der topologischen Isomorphie, d.h., es existiert eine bijektive lineare Abbildung
von
nach
sodass sowohl
als auch
stetig sind.
- Die direkte
Summe
normierter Räume ist genau dann ein Banachraum, wenn jeder der Einzelräume
ein Banachraum ist.
- Satz
von Banach-Steinhaus: Ist
eine Familie stetiger, linearer Operatoren von einem Banachraum in einen normierten Raum, dann folgt aus der punktweisen Beschränktheit die gleichmäßige Beschränktheit.
- Satz
von der offenen Abbildung: Eine stetige lineare Abbildung
zwischen zwei Banachräumen ist genau dann surjektiv, wenn sie offen ist. Ist
bijektiv und stetig, dann ist die inverse Abbildung
ebenfalls stetig. Daraus ergibt sich, dass jeder bijektive beschränkte lineare Operator zwischen Banachräumen ein Isomorphismus ist.
- Satz
vom abgeschlossenen Graphen: Der Graph
einer linearen Abbildung
zwischen zwei Banachräumen ist genau dann im Produkt
abgeschlossen, wenn die Abbildung stetig ist.
- Satz von Banach-Alaoglu: Die abgeschlossene Einheitskugel im Dualraum eines Banachraums ist schwach-*-kompakt.
- Für jeden separablen
Banachraum
existiert ein abgeschlossener Unterraum
von
, sodass
ist.
- Jeder Banachraum ist ein Fréchet-Raum.
Lineare Operatoren
Sind
und
normierte Räume über demselben Körper
,
so wird die Menge aller stetigen
-linearen Abbildungen
mit
bezeichnet.
In unendlichdimensionalen Räumen sind lineare Abbildungen nicht notwendigerweise stetig.
ist ein
-Vektorraum
und durch
ist eine Norm auf
definiert. Ist
ein Banachraum, so auch
.
Ist
ein Banachraum, so ist
eine Banachalgebra mit dem identischen
Operator
als Einselement;
die Multiplikationsoperation ist durch die Komposition linearer Abbildungen
gegeben.
Dualer Raum
Ist
ein normierter Raum und
der zugrunde liegende Körper,
dann ist
selbst ebenfalls ein Banachraum (mit dem Absolutbetrag als
Norm), und man kann den topologischen Dualraum (auch stetigen Dualraum)
definieren durch
.
Er ist in der Regel ein echter Teilraum des algebraischen Dualraums
.
- Ist
ein normierter Raum, so ist
ein Banachraum.
- Sei
ein normierter Raum. Ist
separabel so auch
.
Der topologische Dualraum kann verwendet werden, um eine Topologie auf
zu definieren: die schwache
Topologie. Die schwache Topologie ist nicht äquivalent zur Normtopologie auf
,
wenn der Raum
unendlichdimensional ist. Aus der Konvergenz einer Folge in der Normtopologie
folgt immer die Konvergenz in der schwachen Topologie, umgekehrt im Allgemeinen
nicht. In diesem Sinne ist die Konvergenzbedingung, die sich aus der schwachen
Topologie ergibt, "schwächer".
Es gibt eine natürliche Abbildung
von
nach
(der Bidualraum), definiert durch:
für alle
und
.
Aus dem Satz
von Hahn-Banach folgt, dass für jedes
aus
die Abbildung
stetig ist und daher ein Element von
.
Die Abbildung
ist stets injektiv
und stetig (sogar isometrisch).
Reflexivität
Falls die natürliche Abbildung
zudem noch surjektiv
(und somit ein isometrischer Isomorphismus) ist, so nennt man den normierten
Raum
reflexiv. Es gelten
folgende Zusammenhänge:
- Jeder reflexive normierter Raum ist ein Banachraum.
- Ein Banachraum
ist genau dann reflexiv, wenn
reflexiv ist. Äquivalent zu dieser Aussage ist, dass die Einheitskugel von
in der schwachen Topologie kompakt ist.
- Ist
ein reflexiver normierter Raum,
ein Banachraum und existiert ein beschränkter linearer Operator von
nach
, dann ist
reflexiv.
- Ist
ein reflexiver normierter Raum. Dann ist
genau dann separabel, wenn
separabel ist.
-
Satz von James Für einen Banachraum
sind äquivalent:
ist reflexiv.
mit
, so dass
.
Tensorprodukt
Seien
und
zwei
-Vektorräume.
Das Tensorprodukt
von
und
ist ein
-Vektorraum
,
versehen mit einer bilinearen Abbildung
,
die die folgende universelle Eigenschaft besitzt: Ist
eine beliebige bilineare Abbildung in einen
-Vektorraum
,
so existiert genau eine lineare Abbildung
mit
.
Es gibt verschiedene Möglichkeiten, eine Norm auf dem Tensorprodukt der zugrunde liegenden Vektorräume zu definieren, unter anderem das projektive Tensorprodukt und das injektive Tensorprodukt. Das Tensorprodukt vollständiger Räume ist im Allgemeinen nicht wieder vollständig. Daher versteht man in der Theorie der Banachräume unter einem Tensorprodukt häufig dessen Vervollständigung, welche natürlich von der Wahl der Norm abhängt.
Beispiele
Im Folgenden ist
der Körper
oder
,
ein kompakter Hausdorffraum
und
ein abgeschlossenes Intervall.
und
sind reelle Zahlen mit
und
.
Weiter ist
eine σ-Algebra,
eine Mengenalgebra
und
ein Maß.
| Bezeichnung | Dualraum | reflexiv | schwach
vollständig |
Norm | Name |
|---|---|---|---|---|---|
| ja | ja | Euklidischer Raum | |||
| ja | ja | Raum der endlichdimensionalen Vektoren mit der p-Norm | |||
| ja | ja | Raum der endlichdimensionalen Vektoren mit der Maximumsnorm | |||
| ja | ja | Raum der in p-ter Potenz betragsweise summierbaren Folgen | |||
| nein | ja | Raum der betragsweise summierbaren Folgen | |||
| nein | nein | Raum der beschränkten Folgen | |||
| nein | nein | Raum der konvergenten Folgen | |||
| nein | nein | Raum der Nullfolgen;
isomorph aber nicht isometrisch zu | |||
| nein | ja | Raum der Folgen beschränkter Variation | |||
| nein | ja | Raum der Nullfolgen beschränkter Variation | |||
| nein | nein | Raum der beschränkten Summen; isometrisch isomorph zu
| |||
| nein | nein | Raum der konvergenten Summen; abgeschlossener Unterraum
von | |||
| nein | nein | Raum der beschränkten | |||
| nein | nein | Raum der stetigen Funktionen auf | |||
| ? | nein | ja | Raum der beschränkten endlich-additiven signierten
Maße auf | ||
| ? | nein | ja | Raum der | ||
| ? | nein | ja | Raum der regulären
Borel-Maße;
abgeschlossener Unterraum von | ||
| ja | ja | Raum der in p-ter Potenz Lebesgue-integrierbaren Funktionen | |||
| ? | nein | ja | Raum der Funktionen beschränkter totaler Variation | ||
| ? | nein | ja | Raum der Funktionen beschränkter totaler Variation, deren
Grenzwert bei | ||
| nein | ja | Raum der absolutstetigen
Funktionen; isomorph zum Sobolev-Raum
| |||
| nein | nein | Raum der glatten
Funktionen; isomorph zu |
Einordnung in die Hierarchie mathematischer Strukturen
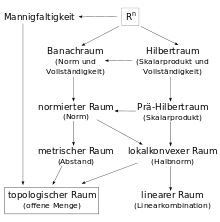
Jeder Hilbertraum ist ein Banachraum, aber nicht umgekehrt. Nach dem Satz von Jordan-von Neumann lässt sich auf einem Banachraum genau dann ein zur Norm verträgliches Skalarprodukt definieren, wenn in ihm die Parallelogrammgleichung gilt.
Einige wichtige Räume in der Funktionalanalysis, zum Beispiel der Raum aller
unendlich oft differenzierbaren Funktionen
oder der Raum aller Distributionen auf
,
sind zwar vollständig, aber keine normierten Vektorräume und daher keine
Banachräume. In Fréchet-Räumen
hat man noch eine vollständige Metrik,
während LF-Räume
vollständige uniforme
Vektorräume sind, die als Grenzfälle von Fréchet-Räumen auftauchen. Es
handelt sich hierbei um spezielle Klassen lokalkonvexer
Räume bzw. topologischer
Vektorräume.
Jeder normierte Raum lässt sich bis auf isometrische Isomorphie eindeutig vervollständigen, das heißt als dichten Unterraum in einen Banachraum einbetten.
Fréchet-Ableitung
Es ist möglich, die Ableitung
einer Funktion
zwischen zwei Banachräumen zu definieren. Intuitiv sieht man, dass, falls
ein Element von
ist, die Ableitung von
im Punkt
eine stetige lineare Abbildung ist, die
nahe
in der Ordnung des Abstandes
approximiert.
Man nennt
(Fréchet)-differenzierbar in
,
falls eine stetige lineare Abbildung
existiert, so dass
gilt. Der Grenzwert
wird hier über alle Folgen
mit nicht-Null-Element aus
gebildet, die gegen 0 konvergieren. Falls der Grenzwert existiert, schreibt man
und nennt es die (Fréchet)-Ableitung
von
in
.
Weitere Verallgemeinerungen der Ableitung ergeben sich analog zur Analysis auf
endlichdimensionalen Räumen. Gemeinsam für alle Ableitungsbegriffe ist aber die
Frage nach der Stetigkeit der linearen Abbildung
Dieser Begriff der Ableitung ist eine Verallgemeinerung der gewöhnlichen
Ableitung von Funktionen ,
da die linearen Abbildungen von
auf
einfach Multiplikationen mit reellen Zahlen sind.
Falls
differenzierbar ist in jedem Punkt
aus
,
dann ist
eine weitere Abbildung zwischen Banachräumen (im Allgemeinen keine
lineare Abbildung!) und kann möglicherweise erneut differenziert werden, wodurch
die höheren Ableitungen von
definiert werden. Die
-te
Ableitung im Punkt
kann somit als multilineare Abbildung
gesehen werden.
Differentiation ist eine lineare Operation im folgenden Sinne: Sind
und
zwei Abbildungen
,
die in
differenzierbar sind, und sind
und
Skalare aus
,
dann ist
differenzierbar in
und es gilt
.
Die Kettenregel
ist in diesem Zusammenhang ebenfalls gültig. Wenn
eine in
und
eine in
differenzierbare Funktion ist, dann ist die Komposition
in
differenzierbar und die Ableitung ist die Komposition der Ableitungen
Auch Richtungsableitungen können auf unendlichdimensionale Vektorräume erweitert werden, an dieser Stelle sei auf das Gâteaux-Differential verwiesen.
Integration Banachraum-wertiger Funktionen
Unter bestimmten Bedingungen ist es möglich Banachraum-wertige Funktionen zu integrieren. Im zwanzigsten Jahrhundert wurden viele verschiedene Zugänge zu einer Integrationstheorie von Banachraum-wertigen Funktionen vorgestellt. Beispiele sind das Bochner-Integral, das Birkhoff-Integral und das Pettis-Integral. In endlichdimensionalen Banachräumen führen diese drei verschiedenen Zugänge zur Integration letztendlich zum selben Integral. Für unendlichdimensionale Banachräume ist dies jedoch im Allgemeinen nicht mehr der Fall. Ferner kann man von gewöhnlichen Maßen zu vektoriellen Maßen, die ihre Werte in Banachräumen annehmen, übergehen und ein Integral bezüglich solcher Maße definieren.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 28.03. 2021