Basis (Vektorraum)

In der linearen Algebra ist eine Basis eine Teilmenge eines Vektorraumes, mit deren Hilfe sich jeder Vektor des Raumes eindeutig als endliche Linearkombination darstellen lässt. Die Koeffizienten dieser Linearkombination heißen die Koordinaten des Vektors bezüglich dieser Basis. Ein Element der Basis heißt Basisvektor. Wenn Verwechslungen mit anderen Basisbegriffen (z.B. der Schauderbasis) zu befürchten sind, nennt man eine solche Teilmenge auch Hamelbasis (nach Georg Hamel). Ein Vektorraum besitzt im Allgemeinen verschiedene Basen, ein Wechsel der Basis erzwingt eine Koordinatentransformation. Die Hamelbasis sollte nicht mit der Basis eines Koordinatensystems verwechselt werden, da diese Begriffe unter bestimmten Bedingungen nicht gleichgesetzt werden können (z.B. bei krummlinigen Koordinaten).

Definition und grundlegende Begriffe

Eine Basis eines Vektorraums ist eine Teilmenge von mit folgenden gleichwertigen Eigenschaften:

Jedes Element von lässt sich als Linearkombination von Vektoren aus darstellen und diese Darstellung ist eindeutig.
ist ein minimales Erzeugendensystem von , jeder Vektor aus lässt sich also als Linearkombination aus darstellen ( ist lineare Hülle von ) und diese Eigenschaft gilt nicht mehr, wenn ein Element aus entfernt wird.
ist eine maximale linear unabhängige Teilmenge von . Wird also ein weiteres Element aus zu hinzugefügt, ist die neue Menge nicht mehr linear unabhängig.
ist ein linear unabhängiges Erzeugendensystem von .

Die Elemente einer Basis heißen Basisvektoren. Ist der Vektorraum ein Funktionenraum, nennt man die Basisvektoren auch Basisfunktionen. Eine Basis lässt sich mit Hilfe einer Indexmenge in der Form $B=\{b_{i}:\;i\in I\}$ beschreiben, eine endliche Basis beispielsweise in der Form $B = \{b_1, \dotsc, b_n\}$ . Wird eine solche Indexmenge benutzt, dann verwendet man jedoch meist zur Bezeichnung der Basis gleich die Familienschreibweise, d.h. $b=(b_{i})_{i\in I}$ statt $B=\{b_{i}:\;i\in I\}$ .

Man beachte, dass in der Familienschreibweise eine Ordnungsrelation auf der Indexmenge eine Anordnung der Basisvektoren erzeugt; heißt dann „geordnete Basis“. Dies macht man sich bei der Beschreibung der Orientierung von Vektorräumen zunutze. Eine Indexmenge mit Ordnungsrelation ermöglicht es, unter den Basen Orientierungsklassen (Händigkeit) einzuführen. Beispiele: abzählbar unendliche Basis $b=(b_{i})_{i\in \mathbb {N} }$ , endliche Basis $b=(b_{1},\dotsc ,b_{n})=(b_{i})_{i\in \{1,\dotsc ,n\}}$ .

Die Koeffizienten, die in der Darstellung eines Vektors als Linearkombination von Vektoren aus der Basis auftreten, nennt man die Koordinaten des Vektors bezüglich . Diese sind Elemente des dem Vektorraum zugrundeliegenden Körpers (z.B. $\mathbb {R}$ oder $\mathbb {C}$ ). Zusammen bilden diese einen Koordinatenvektor $x=(x_{i})_{i\in B}$ , der allerdings in einem anderen Vektorraum liegt, dem Koordinatenraum $K^{B}$ . Achtung: Da die Zuordnung der Koordinaten zu ihren jeweiligen Basisvektoren entscheidend ist, müssen hier – mangels einer gemeinsamen Indexmenge – die Basisvektoren selbst zur Indizierung herangezogen werden.

Obwohl Basen meist als Mengen aufgeschrieben werden, ist daher eine durch eine Indexmenge gegebene „Indizierung“ praktischer. Die Koordinatenvektoren haben dann die Form $x=(x_{i})_{i\in I}$ , der Koordinatenraum ist $K^{I}$ . Ist mit einer Ordnungsrelation versehen, so entsteht auch für den Koordinatenvektor eine Reihenfolge der Koordinaten. Im Beispiel $I=\{1,\dotsc ,n\}$ ist der Koordinatenvektor von der Form $x=(x_{1},\dotsc ,x_{n})$ („Nummerierung“ der Koordinaten). Der Koordinatenraum ist hier $K^{n}$ , bei reellen oder komplexen Vektorräumen also $\mathbb {R} ^{n}$ bzw. $\mathbb {C} ^{n}$ .

Wichtige Eigenschaften

Jeder Vektorraum besitzt eine Basis. Ein Beweis für diese Aussage ist im Abschnitt Existenzbeweis angegeben.
Alle Basen eines Vektorraumes enthalten dieselbe Anzahl von Elementen. Diese Anzahl, die auch eine unendliche Kardinalzahl sein kann, nennt man die Dimension des Vektorraums.
Eine Teilmenge $\{b_{1},\dotsc ,b_{k}\}$ eines -Vektorraumes definiert eindeutig eine lineare Abbildung $K^{k}\to V,\quad e_{i}\mapsto b_{i}$ , wobei $e_{i}$ den -ten Standardeinheitsvektor bezeichnet.

Diese Abbildung ist genau dann

injektiv, wenn die $b_{i}$ linear unabhängig sind;
surjektiv, wenn die $b_{i}$ ein Erzeugendensystem bilden;
bijektiv, wenn die $b_{i}$ eine Basis bilden.

Diese Charakterisierung überträgt sich auf den allgemeineren Fall von Moduln über Ringen, siehe Basis (Modul).

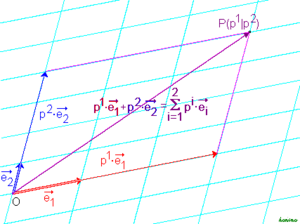
e₁ und e₂ bilden eine Basis der Ebene.

Beispiele

In der euklidischen Ebene $\mathbb {R} ^{2}$ gibt es die so genannte Standardbasis $\{(1,0),(0,1)\}$ . Darüber hinaus bilden in dieser Ebene zwei Vektoren genau dann eine Basis, wenn sie nicht in dieselbe (oder die entgegengesetzte) Richtung zeigen.

Die Standardbasis des Vektorraums $K^{n}$ ist die Menge der kanonischen Einheitsvektoren $\{(1,0,\dotsc ,0),(0,1,0,\dotsc ,0),\dotsc ,(0,\dotsc ,0,1)\}$ .

Die Standardbasis im Raum der Matrizen $K^{m\times n}$ wird durch die Standardmatrizen gebildet, bei denen genau ein Eintrag ist und alle anderen Einträge $0$ sind.

Der Nullvektorraum $\{0\}$ hat Dimension null; seine einzige Basis ist die leere Menge.

Als $\mathbb {R}$ -Vektorraum wird für $\mathbb {C}$ meist die Basis $\{1,i\}$ verwendet. Eine Menge $\{a,b\}\subseteq \mathbb {C} \setminus \{0\}$ ist genau dann eine Basis von $\mathbb {C}$ über $\mathbb {R}$ , wenn ${\tfrac {a}{b}}$ keine reelle Zahl ist. Als $\mathbb {Q}$ -Vektorraum hat $\mathbb {R}$ eine Basis, die man aber nicht explizit angeben kann.

Der Vektorraum der Polynome über einem Körper hat die Basis $\{1,X,X^{2},X^{3},\dotsc \}$ . Es gibt aber auch viele andere Basen, die zwar umständlicher anzuschreiben sind, aber in konkreten Anwendungen praktischer sind, zum Beispiel die Legendre-Polynome.

Im Vektorraum der reellen Zahlenfolgen bilden die Vektoren $\{(1,0,0,0,\dotsc ),(0,1,0,0,\dotsc ),(0,0,1,0,\dotsc ),\dotsc \}$ zwar ein linear unabhängiges System, aber keine Basis, denn es wird zum Beispiel die Folge $(1,1,1,1,\dotsc )$ nicht davon erzeugt, da eine Kombination unendlich vieler Vektoren keine Linearkombination ist.

Beweis der Äquivalenz der Definitionen

Die folgenden Überlegungen skizzieren einen Beweis dafür, dass die vier charakterisierenden Eigenschaften, die in diesem Artikel als Definition des Begriffs Basis genannt werden, äquivalent sind. (Für diesen Beweis wird das Auswahlaxiom oder Lemma von Zorn nicht benötigt.)

Wenn sich jeder Vektor eindeutig als Linearkombination von Vektoren in darstellen lässt, dann ist insbesondere ein Erzeugendensystem (nach Definition).
Wenn nicht minimales Erzeugendensystem ist, dann gibt es eine echte Teilmenge , die auch ein Erzeugendensystem ist. Sei nun $b^{*}$ ein Element von , welches nicht in liegt. Dann lässt sich $b^{*}$ auf mindestens zwei verschiedene Arten als Linearkombination von Vektoren in darstellen, nämlich einmal als Linearkombination von Vektoren in und einmal als $b^{*}=1\cdot b^{*}$ . Es ergibt sich ein Widerspruch und daher ist minimal.
Also gilt (1) → (2).

Jedes minimale Erzeugendensystem muss linear unabhängig sein. Denn wenn nicht linear unabhängig ist, dann gibt es einen Vektor $b^{*}$ in , welcher sich als Linearkombination von Vektoren in $B\setminus \{b^{*}\}$ darstellen lässt. Dann aber lässt sich jede Linearkombination von Vektoren in auch durch eine Linearkombination von Vektoren in $B\setminus \{b^{*}\}$ umschreiben und wäre nicht minimal.
Also gilt (2) → (4).

Jedes linear unabhängige Erzeugendensystem muss eine maximale linear unabhängige Menge sein. Wäre nämlich nicht maximal linear unabhängig, so gäbe es ein $b^{*}$ (das nicht in liegt), welches zusammen mit linear unabhängig wäre. Aber $b^{*}$ lässt sich als Linearkombination von Elementen von darstellen, was der linearen Unabhängigkeit widerspricht.
Also gilt (4) → (3).

Ein maximal linear unabhängiges System ist ein Erzeugendensystem: Sei $b^{*}$ ein beliebiger Vektor. Wenn $b^{*}$ in enthalten ist, dann lässt sich $b^{*}$ als Linearkombination von Elementen von schreiben. Wenn aber $b^{*}$ nicht in enthalten ist, dann ist die Menge $B\ \cup \{b^{*}\}$ eine echte Obermenge von und damit nicht mehr linear unabhängig. Die Vektoren $b_1, \dotsc, b_n$ , die in einer möglichen linearen Abhängigkeit $a_{1}b_{1}+\dotsb +a_{n}b_{n}=0$ vorkommen, können nicht alle aus sein, daher muss einer davon (sagen wir $b_{1}$ ) gleich $b^{*}$ sein, mit $a_{1}$ ungleich 0. Daher ist $b^{*}=-{\tfrac {1}{a_{1}}}(a_{2}b_{2}+\dotsb +a_{n}b_{n})$ . Die Eindeutigkeit dieser Darstellung folgt aus der linearen Unabhängigkeit von .
Also gilt (3) → (1).

Existenzbeweis

Mit dem Lemma von Zorn kann man beweisen, dass jeder Vektorraum eine Basis haben muss, auch wenn man sie oft nicht explizit angeben kann.

Sei ein Vektorraum. Man möchte eine maximale linear unabhängige Teilmenge des Vektorraums finden. Es liegt also nahe, das Mengensystem

$P:=\{X\subseteq V:\;X{\text{ linear unabhängig}}\}\,$

zu betrachten, das durch die Relation $\subseteq$ halbgeordnet wird. Man kann nun zeigen:

ist nicht leer (zum Beispiel enthält die leere Menge). Besteht nicht nur aus dem Nullvektor, dann ist zusätzlich auch jede Einermenge $\{v\}$ mit in und $v\neq \mathbf {0}$ ein Element von .
Für jede Kette $C\subseteq P$ ist auch $\bigcup C=\bigcup _{X\in C}X=\{v:\exists X\in C:v\in X\}$ in .

Aus dem Lemma von Zorn folgt nun, dass ein maximales Element hat. Die maximalen Elemente von sind nun aber genau die maximalen linear unabhängigen Teilmengen von , also die Basen von . Daher hat eine Basis und es gilt darüber hinaus, dass jede linear unabhängige Teilmenge von in einer Basis von enthalten ist.

Basisergänzungssatz

Ist $T\subset V$ eine vorgegebene Menge linear unabhängiger Vektoren und geht man in obigem Beweis von

$P:=\{X\subseteq V:\;T\subset X,\,X{\text{ linear unabhängig}}\}\,$

aus, so erhält man die Aussage, dass in einem maximalen Element von enthalten ist. Da sich ein solches maximales Element wieder als eine Basis von erweist, ist gezeigt, dass man jede Menge linear unabhängiger Vektoren zu einer Basis von ergänzen kann. Diese Aussage nennt man Basisergänzungssatz.

Weitere Aussagen über Basen

Austauschlemma von Steinitz (nach E. Steinitz): Sind $v_{1},\dotsc ,v_{n}$ eine Basis eines Vektorraumes und ein weiterer vom Nullvektor verschiedener Vektor aus , so kann man einen der Basisvektoren gegen „austauschen“, d.h., es existiert ein Index $1\leq i\leq n$ , sodass $v_{1},\dotsc ,v_{i-1},w,v_{i+1},\dotsc ,v_{n}$ ebenfalls eine Basis von ist.
Diese Aussage wird häufig benutzt, um zu zeigen, dass alle Basen eines Vektorraumes aus gleich vielen Vektoren bestehen.
Jeder Vektorraum ist ein freies Objekt über seiner Basis. Dies ist eine universelle Eigenschaft von Vektorräumen im Sinne der Kategorientheorie. Konkret heißt dies:

Eine lineare Abbildung eines Vektorraums in einen anderen Vektorraum ist bereits durch die Bilder der Basisvektoren vollständig bestimmt.
Jede beliebige Abbildung der Basis in den Bildraum definiert eine lineare Abbildung.

In einem -dimensionalen Vektorraum über einem endlichen Körper mit Elementen gibt es

${\frac {1}{d!}}\prod _{k=0}^{d-1}\left(q^{d}-q^{k}\right)$

verschiedene Basen.

Basisbegriffe in speziellen Vektorräumen

Reelle und komplexe Vektorräume tragen meist zusätzliche topologische Struktur. Aus dieser Struktur kann sich ein Basisbegriff ergeben, der vom hier beschriebenen abweicht.

Basis und duale Basis im dreidimensionalen euklidischen Vektorraum

In der klassischen Mechanik wird der Anschauungsraum mit dem drei-dimensionalen euklidischen Vektorraum (V³, ·) modelliert, wodurch dieser eine besondere Relevanz bekommt. Euklidische Vektorräume sind u.a. dadurch definiert, dass es in ihnen ein Skalarprodukt „·“ gibt, wodurch diese Vektorräume besondere und erwähnenswerte Eigenschaften erhalten.

Im dreidimensionalen euklidischen Vektorraum gibt es zu jeder Basis ${\vec {b}}_{1,2,3}$ genau eine duale Basis ${\vec {b}}^{1,2,3}$ , sodass mit dem Kronecker-Delta δ gilt: ${\vec {b}}_{i}\cdot {\vec {b}}^{j}=\delta _{i}^{j}.$ Bei einer Orthonormalbasis sind alle Basisvektoren auf Länge eins normiert und paarweise orthogonal. Dann stimmen Basis und duale Basis überein.

Jeder Vektor ${\vec {v}}$ lässt sich nun als Linearkombination der Basisvektoren darstellen:

${\vec {v}}=\sum _{i=1}^{3}({\vec {v}}\cdot {\vec {b}}^{i}){\vec {b}}_{i}=\sum _{i=1}^{3}({\vec {v}}\cdot {\vec {b}}_{i}){\vec {b}}^{i}$

Denn die Differenzvektoren von ${\vec {v}}$ zu den Vektoren rechts der Gleichheitszeichen sind Nullvektoren.

Der dreidimensionale euklidische Vektorraum ist ein vollständiger Skalarproduktraum.

Hamel- und Schauderbasis in Skalarprodukträumen

Beim Studium von reellen oder komplexen Skalarprodukträumen, besonders von Hilberträumen gibt es noch eine andere, dort zweckmäßigere Art, die Elemente des Raumes darzustellen. Eine Basis besteht dabei aus paarweise orthogonalen Einheitsvektoren, und es werden nicht nur endliche, sondern auch unendliche Summen (sog. Reihen) von Basisvektoren zugelassen. Ein solches vollständiges Orthonormalsystem ist in einem unendlichdimensionalen Raum nie eine Basis im hier definierten Sinn, zur besseren Unterscheidung spricht man auch von Schauderbasis. Der im vorliegenden Artikel beschriebene Basistyp wird zur Unterscheidung auch Hamelbasis genannt.

Auerbachbasen

Eine Auerbachbasis ist eine Hamelbasis für einen dichten Unterraum in einem normierten Vektorraum, sodass der Abstand jedes Basisvektors vom Erzeugnis der übrigen Vektoren gleich seiner Norm ist.

Abgrenzung der Basisbegriffe

Sowohl eine Hamelbasis als auch eine Schauderbasis ist eine linear unabhängige Menge von Vektoren.
Eine Hamelbasis oder einfach Basis, wie sie in diesem Artikel beschrieben ist, bildet ein Erzeugendensystem des Vektorraums, d.h., ein beliebiger Vektor des Raums lässt sich als Linearkombination aus endlich vielen Vektoren der Hamelbasis darstellen.
Bei einem endlichdimensionalen reellen oder komplexen Skalarproduktraum ist eine Orthonormalbasis (d.h. ein minimales Erzeugendensystem aus normierten, zueinander senkrechten Vektoren) zugleich Hamel- und Schauderbasis.
Bei einem unendlichdimensionalen, vollständigen reellen oder komplexen Skalarproduktraum (speziell also in einem unendlichdimensionalen Hilbertraum) ist eine Schauderbasis nie eine Hamelbasis und umgekehrt. Im unendlichdimensionalen Fall lässt sich eine Hamelbasis häufig nicht einmal orthonormieren.
Die Hamelbasis eines unendlichdimensionalen, separablen Hilbertraumes besteht aus überabzählbar vielen Elementen. Eine Schauderbasis hingegen besteht in diesem Fall aus abzählbar vielen Elementen. Es gibt mithin keinen Hilbertraum von Hamel-Dimension $\aleph _{0}$ .
In Hilberträumen ist mit Basis (ohne Zusatz) meistens eine Schauderbasis gemeint, in Vektorräumen ohne Skalarprodukt immer eine Hamelbasis.

Siehe auch

Literatur

Peter Knabner, Wolf Barth: Lineare Algebra. Grundlagen und Anwendungen. Springer Spektrum, Berlin/Heidelberg 2013, ISBN 978-3-642-32185-6.
Uwe Storch, Hartmut Wiebe: Lehrbuch der Mathematik. Band II: Lineare Algebra. BI-Wissenschaft, Mannheim u.a. 1990, ISBN 978-3-411-14101-2.

Basierend auf einem Artikel in:

Wikipedia.de