Legendre-Polynom

Die Legendre-Polynome (nach Adrien-Marie Legendre), auch zonale Kugelfunktionen genannt, sind spezielle Polynome, die auf dem Intervall [-1,1] ein orthogonales Funktionensystem bilden. Sie sind die partikulären Lösungen der legendreschen Differentialgleichung. Eine wichtige Rolle spielen die Legendre-Polynome in der theoretischen Physik, insbesondere in der Elektrodynamik und in der Quantenmechanik und im Bereich der Filtertechnik bei den Legendre-Filtern.

Herkunft

Konstruktion orthogonaler Polynome

Für ein Intervall I = [a,b] und eine darauf gegebene Gewichtsfunktion $\varrho(x)$ ist eine Folge (P_n) von reellen Polynomen $P_n\in\R[X]$ orthogonal, wenn sie die Orthogonalitätsbedingung

$\int \limits _{a}^{b}\varrho (x)\,P_{n}(x)\,P_{m}(x)\,{\mathrm {d}}x=0$

für alle $m, n\in\Bbb N_0$ mit $m\neq n$ erfüllt.

Für das Intervall I = [-1,1] zusammen mit der einfachsten aller Gewichtsfunktionen $\varrho(x) = 1$ können solche orthogonalen Polynome mit Hilfe des Gram-Schmidtschen Orthogonalisierungsverfahren ausgehend von den Monomen $(x^n)_{n\in \Bbb N}$ iterativ erzeugt werden. Die Legendre-Polynome ergeben sich, wenn dabei zusätzlich P_n(1) = 1 gefordert wird.

Legendresche Differentialgleichung

Die Legendre-Polynome P_n(x) sind Lösungen der legendreschen Differentialgleichung

$\left(1-x^2\right)\,f''(x)-2x\,f'(x)+n(n+1)\,f(x)=0,\quad n\in\mathbb{N}_0,$

welche auch in der Form

$\frac{\mathrm{d}}{\mathrm{d}x} \left[ \left(1-x^2\right) \, f'(x) \right] + n(n+1) \, f(x) = 0$

geschrieben werden kann. Die allgemeine Lösung dieser Differentialgleichung lautet

$f(x)=A\,P_n(x)+B\,Q_n(x)$

mit den beiden linear unabhängigen Funktionen P_n(x) und Q_n(x) . Man bezeichnet die Legendre-Polynome P_n(x) daher auch als Legendre-Funktionen 1. Art und Q_n(x) als Legendre-Funktionen 2. Art, denn diese sind keine Polynome mehr.

Darüber hinaus existiert noch eine verallgemeinerte Legendresche Differentialgleichung, deren Lösungen zugeordnete Legendrepolynome heißen.

Legendre-Polynome

Das -te Legendre-Polynom hat den Grad und ist aus $\Bbb Q[x]$ , d.h., es hat rationale Koeffizienten. Für die Legendre-Polynome gibt es mehrere Darstellungsformen.

Monomdarstellung

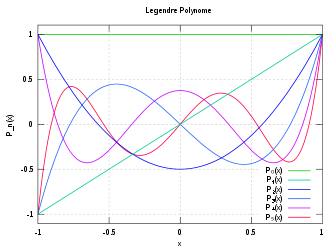
Die ersten sechs Legendre–Polynome

Die ersten Legendre-Polynome lauten:

$P_0(x) = 1\,$

$P_1(x) = x\,$

$P_2(x) = \frac{1}{2} (3x^2 - 1)$

$P_3(x) = \frac{1}{2} (5x^3 - 3x)$

$P_4(x) = \frac{1}{8}(35x^4-30x^2+3)$

$P_5(x) = \frac{1}{8}(63x^5-70x^3+15x)$

$P_6(x) = \frac{1}{16}(231x^6-315x^4+105x^2-5)$

Das -te Legendre Polynom lautet

$P_n(x) = \sum_{k=0}^{\lfloor n/2\rfloor} (-1)^k \frac{(2n - 2k)! \ }{(n-k)! \ (n-2k)! \ k! \ 2^n} x^{n-2k}$

mit der Gauß-Klammer

$\left\lfloor \frac{n}{2}\right\rfloor = \begin{cases} \frac{n}{2} & n \ \text{gerade}\\ \frac{n-1}{2} & n \ \text{ungerade} \end{cases}$

Rodrigues-Formel

$P_{n}(x)={\frac {1}{2^{n}\,n!}}\cdot {\frac {{\mathrm {d}}^{n}}{{\mathrm {d}}x^{n}}}\left[(x^{2}-1)^{n}\right]$

Die Rodrigues-Formel kann man mit der Formel von Faà di Bruno auswerten und erhält wieder die explizite Form des -ten Legendre-Polynoms.

Integraldarstellung

Für alle $x \in \mathbb{C} \setminus \{+1, -1\}$ gilt

$P_n(x) = \frac{1}{\pi} \int_0^\pi \left[x + \sqrt{x^2 - 1} \cos\varphi\right]^n \, \mathrm{d}\varphi$

Rekursionsformeln

Für die Legendre-Polynome gelten folgende Rekursionsformeln:

${\begin{aligned}(n+1)P_{{n+1}}(x)&=(2n+1)xP_{n}(x)-nP_{{n-1}}(x)\,\,\,\,\,\quad \quad (n=1,2,\ldots ;P_{0}=1;P_{1}=x)\\(x^{2}-1){\frac {{\mathrm {d}}}{{\mathrm {d}}x}}P_{n}(x)&=nxP_{n}(x)-nP_{{n-1}}(x)\end{aligned}}$

Die erste rekursive Formel lässt sich mittels der Substitution n'=n+1 in folgender, häufig zu findenden Weise darstellen:

$nP_{{n}}(x)=(2n-1)xP_{{n-1}}(x)-(n-1)P_{{n-2}}(x)\,\,\,\,\,\qquad (n=2,3,\ldots ;P_{0}=1;P_{1}=x)$

Durch Anwendung der Ableitungsregel für Ausdrücke der Art y = x^n mit $y'=nx^{n-1} = nx^{-1}y$ , bzw. $y^{(m)} = (n-m+1)x^{-1}y^{(m-1)}$ ergibt sich folgende rekursive Darstellung der Legendre-Polynome, welche auch die Ableitungen dieser Polynome berücksichtigt:

$(n-m)P_{{n}}^{{(m)}}(x)=(2n-1)xP_{{n-1}}^{{(m)}}(x)-(n-1+m)P_{{n-2}}^{{(m)}}(x)\,\,\,\,\,\qquad (n>1;\,\,m=0\ldots n-1)$

Die Anfangsbedingungen lauten $P_{m}^{{(m)}}(x)={\frac {(2m)!}{2^{m}m!}}$ und $P_{{k}}^{{(m)}}(x)={0}\,\,\,\,\,\qquad (k<m)$ .

Bei m=0 ergibt sich wiederum die weiter oben angegebene Formel mit ihren Anfangsbedingungen.

Eigenschaften

Vollständiges Orthogonalsystem

Man betrachte den Hilbertraum $V:= L^2([-1,1]; \R)$ der quadratintegrierbaren auf [-1,1] definierten reellwertigen Funktionen ausgestattet mit dem Skalarprodukt

$\langle f,g\rangle =\int _{{-1}}^{1}f(x)g(x){\mathrm {d}}x$ .

Die Familie (P_n)_n der Legendre-Polynome bildet auf $(V, \langle\cdot,\cdot\rangle)$ ein vollständiges Orthogonalsystem, sie sind also ein Spezialfall von orthogonalen Polynomen. Normiert man diese, so bilden sie ein vollständiges Orthonormalsystem auf .

Es gilt

$\int \limits _{{-1}}^{{1}}P_{n}(x)P_{m}(x)\,{\mathrm {d}}x={\frac {2}{2n+1}}\delta _{{nm}}$ ,

wobei $\delta_{nm}$ das Kronecker-Delta bezeichnet. Dabei bedeutet die Vollständigkeit, dass sich jede Funktion $f\in V$ in der von $\langle\cdot,\cdot\rangle$ erzeugten Normtopologie nach Legendre-Polynomen „entwickeln“ lässt:

$f(x) = \sum_{n=0}^\infty c_n \, P_n(x)$

mit den Entwicklungskoeffizienten

$c_{n}={\frac {2\,n+1}{2}}\,\int \limits _{{-1}}^{1}f(x)\,P_{n}(x)\,{\mathrm {d}}x.$

In der physikalischen oder technischen Literatur wird die Vollständigkeit gern wie folgt als Distributionsgleichung geschrieben:

$\sum_{n=0}^\infty \frac{2\,n+1}{2} \, P_n(x') \, P_n(x) = \delta(x'-x)$ ,

wobei $\delta$ die diracsche Delta-Distribution ist. Eine solche Distributionsgleichung ist immer so zu lesen, dass beide Seiten dieser Gleichung auf Testfunktionen anzuwenden sind. Wendet man die rechte Seite auf eine solche Testfunktion $x\mapsto f(x)$ an, so erhält man f(x') . Zur Anwendung der linken Seite muss man definitionsgemäß mit f(x) multiplizieren und anschließend über integrieren. Dann erhält man aber genau obige Entwicklungsformel (mit an Stelle von ). Orthogonalität und Vollständigkeit lassen sich daher kurz und prägnant wie folgt schreiben:

Orthogonalität: $\langle P_n, P_m \rangle = 0$ für $m\neq n$ .
Vollständigkeit: $f(x) = \sum_{n=0}^\infty \frac{2n+1}{2}\langle f,P_n\rangle \, P_n(x)$ für alle $f\in L^2([-1,1]; \R)$ (im Sinne der $L^{2}$ -Konvergenz).

Nullstellen

P_n(x) hat auf dem Intervall I = [-1,1] genau einfache Nullstellen. Sie liegen symmetrisch zum Nullpunkt der Abszisse, da Legendre-Polynome entweder gerade oder ungerade sind. Zwischen zwei benachbarten Nullstellen von P_n(x) liegt genau eine Nullstelle von $P_{n-1}(x)$ . In welchem Verhältnis eine Nullstelle von $P_{n-1}(x)$ das Intervall zwischen zwei Nullstellen von P_n(x) teilt, oder auch umgekehrt bis auf die äußeren von P_n(x) , ist dabei sehr variabel.

Die Bestimmung der Nullstellen der Legendre-Polynome ist in der numerischen Mathematik eine häufige Aufgabe, da sie eine zentrale Rolle bei der Gauß-Legendre-Quadratur oder der unter „Vollständiges Orthogonalsystem“ erwähnten Entwicklung „beliebiger“ Funktionen nach Polynomen spielen. Es gibt zwar zahlreiche Tabellenwerke dafür, aber oft ist ihr Gebrauch mit Unannehmlichkeiten verbunden, weil man für eine flexible Reaktion eine Vielzahl an Tabellen in geeigneten Genauigkeiten vorhalten müsste. Bei der Nullstellensuche ist die Kenntnis des Intervalls nur von beschränktem Wert bei der Wahl eines Iterationsanfangs, zumal auch noch die Kenntnis der Nullstellen eines anderen Polynoms erforderlich ist. Eine mit zunehmendem genauer werdende Näherung der -ten Nullstelle von P_n(x) ist gegeben durch:

$x_k = \cos\left(\pi\,\frac{4k-1}{4n+2}\right),\quad k=1,\ldots,n.$

Für beispielsweise $P_{10}(x)$ werden so alle Nullstellen auf wenigstens zwei Dezimalstellen genau abgeschätzt, mit Fehlern zwischen 0{,}00102 und 0{,}00016 , während das kleinste Nullstellenintervall von $P_{9}(x)$ nur 0{,}13 ist. Bei $P_{20}(x)$ sind bereits drei Dezimalstellen sicher, mit Fehlern zwischen 0{,}00028 und 0{,}00002 , während die beste Einschachtelung durch $P_{19}(x)$ nur 0{,}032 ist. Der maximale Schätzfehler für $P_{200}(x)$ ist nur 0{,}0000031 bei den beiden fünften Nullstellen von außen, deren exakter Betrag mit $0{,}99722851428\ldots$ beginnt.

Mit einem solchen Startwert und den beiden ersten „Rekursionsformeln“ lassen sich mit einem Rechengang sowohl der Funktionswert als auch dessen Ableitung bestimmen. Mithilfe des Newton-Verfahrens lassen sich alle Nullstellen bis auf die beiden äußeren mit mehr als quadratischer Konvergenz finden, da sich die Nullstellen in unmittelbarer Nähe der Wendestellen befinden. Die beiden äußeren Nullstellen konvergieren „nur“ quadratisch, d.h. ein anfänglicher Abstand zur Nullstelle von 0{,}00102 verkleinert sich nach einer Iteration zunächst auf ungefähr $0{,}00102^{2}$ , dann auf $0{,}00102^{4},0{,}00102^{8}$ und $0{,}00102^{{16}}$ .

Die angegebene Abschätzung ist Teil eines sehr kurzen Algorithmus, die sowohl alle Nullstellen eines Legendre-Polynoms als auch die passenden Gewichte für die Gauß-Legendre-Quadratur liefert.

Allgemeine Eigenschaften

Für jedes $n\in \mathbb {N}$ und jedes $x \in [-1,1]$ gilt:

$\begin{align} P_n(1) &= 1\\[.3em] P_n(-x) &= (-1)^n \, P_n(x)\\[.3em] P_{2\,n+1}(0) &= 0 \end{align}$

Erzeugende Funktion

Für alle $x\in \mathbb {R}$ , $z \in \mathbb{C}$ , |z| < 1 gilt

$(1 - 2xz + z^2)^{-1/2} = \sum_{n=0}^\infty P_n(x) z^n\ .$

Dabei hat die Potenzreihe auf der rechten Seite für $-1 \le x \le +1$ den Konvergenzradius 1.

Die Funktion $z \mapsto (1 - 2xz + z^2)^{-1/2}$ wird daher als erzeugende Funktion der Legendre-Polynome $P_{n}$ bezeichnet.

Der in der Physik oft auftretende Term $1/|\vec{x}-\vec{x}\,'|$ (z.B. in den Potentialen der newtonschen Gravitation oder der Elektrostatik; Multipolentwicklung) lässt sich damit in eine Potenzreihe entwickeln für $\tfrac{|\vec{x}\,'|}{|\vec{x}|}=\tfrac{r\,'}{r}<1$ :

$\begin{align} \frac{1}{|\vec{x}-\vec{x}\,'|} &=\frac{1}{\sqrt{\vec{x\,}^{2}-2\vec{x}\cdot\vec{x}\,'+\vec{x}\,'^{2}}} =\frac{1}{\sqrt{r^{2}-2rr\,'\cos\alpha+r\,'^{2}}} =\frac{1}{r\sqrt{1-2\frac{r'}{r}\cos\alpha+(\frac{r'}{r})^{2}}} \\&=\frac{1}{r}\sum_{n=0}^{\infty}\left(\frac{r\,'}{r}\right)^{n}P_{n}(\cos\alpha) \end{align}$

Legendre-Funktionen 2. Art

Die Rekursionsformeln der Legendre-Polynome gelten auch für die Legendre-Funktionen 2. Art, so dass diese sich iterativ mit der Angabe der ersten bestimmen lassen:

$Q_{0}(x)={\frac {1}{2}}\,\ln \left({\frac {1+x}{1-x}}\right)=\operatorname {artanh}(x)$

$Q_{1}(x)={\frac {x}{2}}\,\ln \left({\frac {1+x}{1-x}}\right)-1=x\operatorname {artanh}(x)-1$

$Q_{2}(x)={\frac {3\,x^{2}-1}{4}}\,\ln \left({\frac {1+x}{1-x}}\right)-{\frac {3\,x}{2}}={\frac 32}\left(\left(x^{2}-{\frac 13}\right)\operatorname {artanh}(x)-x\right)$

$Q_3(x) = \frac{5\,x^3 - 3\,x}{4} \, \ln\left( \frac{1+x}{1-x} \right) - \frac{5\,x^2}{2} + \frac{2}{3}$

Hierbei ist für den Logarithmus der Hauptzweig zu verwenden wodurch sich Singularitäten bei $x=\pm 1$ und in der komplexe Ebene Verzweigungsschnitte entlang $(-\infty,-1)$ und $(1,\infty)$ ergeben.

Basierend auf einem Artikel in:

Wikipedia.de