Newtonverfahren

Das Newtonverfahren, auch Newton-Raphson-Verfahren (benannt nach Sir Isaac Newton 1669 und Joseph Raphson 1690), ist in der Mathematik ein häufig verwendeter Approximationsalgorithmus zur numerischen Lösung von nichtlinearen Gleichungen und Gleichungssystemen. Im Falle einer Gleichung mit einer Variablen lassen sich zu einer gegebenen stetig differenzierbaren Funktion $f\colon \mathbb {R} \to \mathbb {R}$ Näherungswerte zu Lösungen der Gleichung f(x)=0 , d.h. Näherungen der Nullstellen dieser Funktion finden. Die grundlegende Idee dieses Verfahrens ist, die Funktion in einem Ausgangspunkt zu linearisieren, d.h. ihre Tangente zu bestimmen, und die Nullstelle der Tangente als verbesserte Näherung der Nullstelle der Funktion zu verwenden. Die erhaltene Näherung dient als Ausgangspunkt für einen weiteren Verbesserungsschritt. Diese Iteration erfolgt, bis die Änderung in der Näherungslösung eine festgesetzte Schranke unterschritten hat. Das Iterationsverfahren konvergiert im günstigsten Fall asymptotisch mit quadratischer Konvergenzordnung, die Zahl der korrekten Dezimalstellen verdoppelt sich dann in jedem Schritt.

Formal ausgedrückt, wird ausgehend von einem Startwert $x_{0}$ die Iteration

$x_{n+1}=x_{n}-{\frac {f(x_{n})}{f'(x_{n})}}$

wiederholt, bis eine hinreichende Genauigkeit erzielt wird.

Newtonverfahren für reelle Funktionen einer Veränderlichen

Historisches über das Newton-Verfahren

Isaac Newton verfasste im Zeitraum 1664 bis 1671 die Arbeit „Methodus fluxionum et serierum infinitarum“ (latein. für: Von der Methode der Fluxionen und unendlichen Folgen). Darin erklärt er einen neuen Algorithmus zum Lösen einer polynomialen Gleichung am Beispiel $y^{3}-2y-5=0$ . Dazu kann man leicht den Punkt y=2 als erste Näherung raten. Newton machte den Ansatz y=2+p mit einem als „klein“ angenommenen und setzte diesen in die Gleichung ein:

Nach den binomischen Formeln gilt

$y^{3}=(2+p)^{3}=8+12p+6p^{2}+p^{3}\$

$\ 2y=2(2+p)=4+2p$

$\Rightarrow \ 0=y^{3}-2y-5=-1+10p+6p^{2}+p^{3}$ .

Da „klein“ sein soll, können die Terme höherer Ordnung gegenüber den linearen und konstanten vernachlässigt werden, womit 10p-1=0 bzw. p=0{,}1 übrig bleibt. Wir können nun dieses Vorgehen wiederholen und p=0{,}1+q ansetzen, in die zweite Gleichung einsetzen, höhere Terme weglassen und $q=-0{,}061/11{,}23=-0{,}0054\dots$ erhalten.

Joseph Raphson beschrieb 1690 in der Arbeit „Analysis Aequationum universalis“ diesen Rechenprozess formal und illustrierte den Formalismus an der allgemeinen Gleichung dritten Grades, wobei er die nachfolgende Iterationsvorschrift fand.

Die abstrakte Form des Verfahrens mit Benutzung der Ableitung $x_{n+1}=x_{n}-{\frac {f(x_{n})}{f'(x_{n})}}$ stammt von Thomas Simpson.

Konstruktion am Graphen

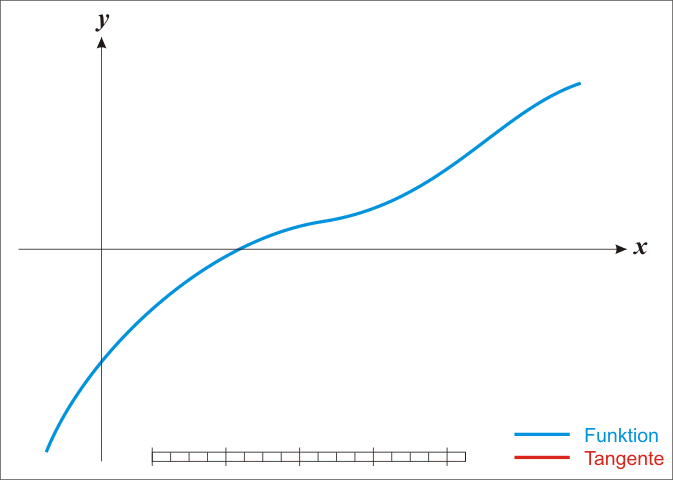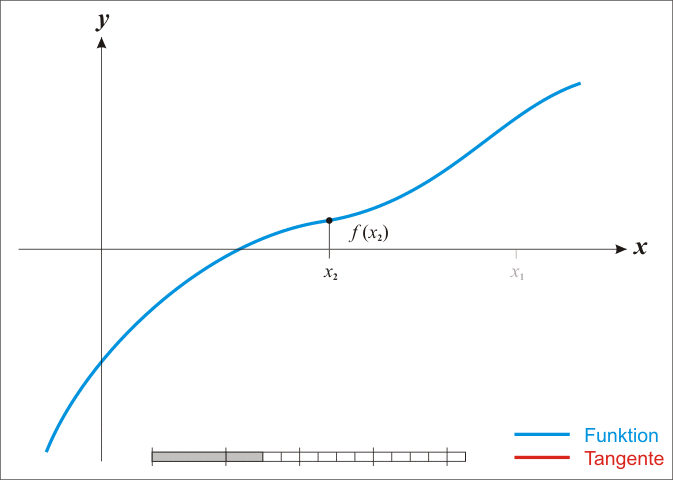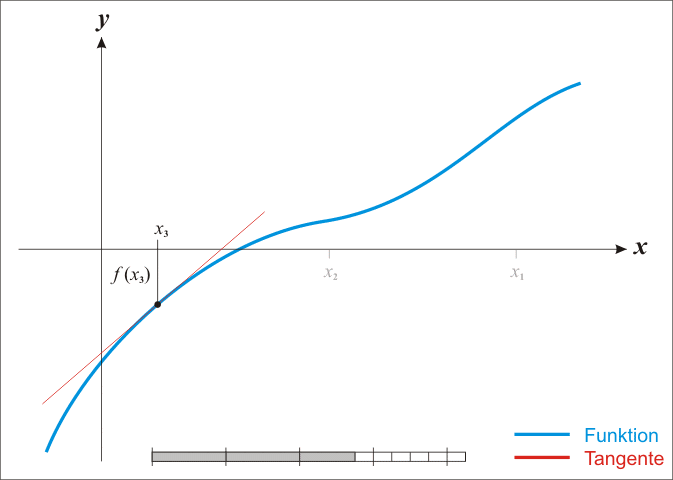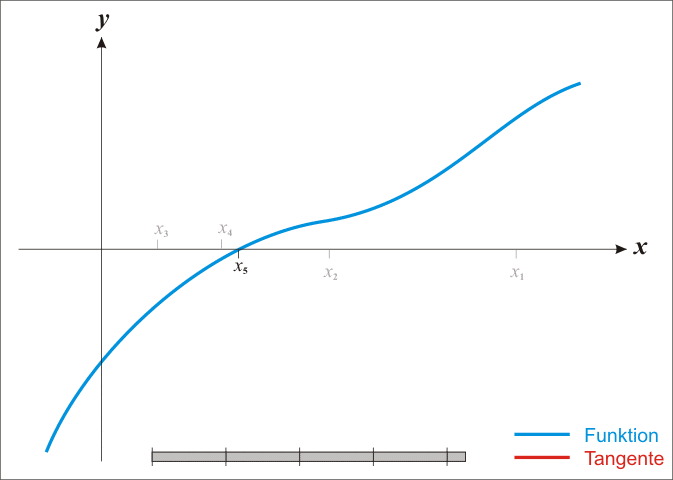
Animation: Iteration mit dem newtonschen Verfahren

Anschaulich gelangt man wie folgt zu diesem Verfahren: Sei $f\colon \mathbb {R} \to \mathbb {R}$ eine stetig differenzierbare reelle Funktion, von der wir eine Stelle $x_{n}$ im Definitionsbereich mit „kleinem“ Funktionswert kennen. Wir wollen einen Punkt $x_{n+1}$ nahe $x_{n}$ finden, der eine verbesserte Näherung der Nullstelle darstellt. Dazu linearisieren wir die Funktion an der Stelle $x_{n}$ , d.h. wir ersetzen sie durch ihre Tangente im Punkt $P(x_{n}\,;\,f(x_{n}))$ mit Anstieg $f^{\prime }(x_{n})$ .

Die Tangente ist durch die Funktion $t(x_{n}+h):=f(x_{n})+f^{\prime }(x_{n})h$ gegeben. Setzen wir $h=x-x_{n}$ ein, so erhalten wir

$t(x):=f(x_{n})+f^{\prime }(x_{n})(x-x_{n})$ .

Wir wählen als $x_{n+1}$ die einzige Nullstelle dieser linearen Funktion,

$0=t(x_{n+1})=f(x_{n})+f^{\prime }(x_{n})(x_{n+1}-x_{n})\quad \Rightarrow \quad x_{n+1}=x_{n}-f(x_{n})/f'(x_{n})$ .

Wenden wir diese Konstruktion mehrfach an, so erhalten wir aus einer ersten Stelle $x_{0}$ eine unendliche Folge von Stellen $(x_{n})_{n\in \mathbb {N} }$ , die durch die Rekursionsvorschrift

$x_{n+1}:=N_{f}(x_{n}):=x_{n}-{\frac {f(x_{n})}{f'(x_{n})}}$

definiert ist. Diese Vorschrift wird auch als Newtoniteration bezeichnet, die Funktion $N_{f}$ als Newtonoperator. Die Newtoniteration ist ein spezieller Fall einer Fixpunktiteration, falls die Folge gegen $\xi =\lim _{n\to \infty }x_{n}\,$ konvergiert, so gilt $\xi =N_{f}(\xi )=\xi -f(\xi )/f'(\xi )$ und daher $f(\xi )=0$ .

Die Kunst der Anwendung des Newtonverfahrens besteht darin, geeignete Startwerte $x_{0}$ zu finden. Je mehr über die Funktion bekannt ist, desto kleiner lässt sich die notwendige Menge von Startwerten gestalten.

Viele nichtlineare Gleichungen haben mehrere Lösungen, so hat ein Polynom -ten Grades bis zu Nullstellen. Will man alle Nullstellen in einem bestimmten Bereich $D\subseteq \mathbb {R}$ ermitteln, so muss zu jeder Nullstelle ein passender Startwert in gefunden werden, für den die Newtoniteration konvergiert. Dazu könnte man z.B. per Bisektion genügend kleine isolierende Intervalle zu jeder Nullstelle bestimmen.

Erstes Beispiel

Die Quadratwurzel einer Zahl a>0 ist die positive Nullstelle der Funktion $f(x)=1-a/x^{2}$ . Diese Funktion hat die Ableitung $f^{\prime }(x)=2a/x^{3}$ , die Newtoniteration erfolgt also nach der Vorschrift

$x_{n+1}:=N_{f}(x_{n})=x_{n}-{\frac {1-a/x_{n}^{2}}{2a/x_{n}^{3}}}=x_{n}-{\frac {x_{n}^{3}}{2a}}+{\frac {x_{n}}{2}}={\frac {x_{n}}{2}}\left(3-{\frac {x_{n}^{2}}{a}}\right)$

Der Vorteil dieser Vorschrift gegenüber dem Wurzelziehen nach Heron (siehe unten) ist, dass es divisionsfrei ist, sobald einmal der Kehrwert von bestimmt wurde. Als Startwert wurde in der Tabelle $x_{0}:=(1+a)/2$ gewählt. Die Iterierten wurden an der ersten ungenauen Stelle abgeschnitten. Es ist zu erkennen, dass nach wenigen Schritten die Anzahl gültiger Stellen schnell wächst.

n	$x_{n}$ bei	$x_{n}$ bei	$x_{n}$ bei
0
1
2
3
4
5
6
7
8

Betrachten wir die Differenz $x_{n+1}-{\sqrt {a}}$ zum Grenzwert im (n+1) -ten Schritt, so kann mittels der binomischen Formeln die Differenz im -ten Schritt zweimal abgespalten werden:

$x_{n+1}-{\sqrt {a}}={\frac {3}{2}}x_{n}-{\frac {x_{n}^{3}}{2a}}-{\frac {3}{2}}{\sqrt {a}}+{\frac {{\sqrt {a}}^{3}}{2a}}=(x_{n}-{\sqrt {a}})\cdot \left({\frac {3}{2}}-{\frac {x_{n}^{2}+x_{n}{\sqrt {a}}+a}{2a}}\right)$

$=(x_{n}-{\sqrt {a}})\cdot {\frac {a-x_{n}^{2}+a-x_{n}{\sqrt {a}}}{2a}}=-(x_{n}-{\sqrt {a}})^{2}\cdot {\frac {x_{n}+2{\sqrt {a}}}{2a}}$

Nach der Ungleichung vom arithmetischen und geometrischen Mittel gilt $0<{\sqrt {a}}\leq {\tfrac {1+a}{2}}$ , so dass der zweite Faktor sinnvoll durch 3/2(1+a) beschränkt werden kann. Ist die Differenz im -ten Schritt eine kleine Zahl, so ist die Differenz im (n+1) -ten Schritt proportional zum Quadrat davon, also wesentlich kleiner. So entsteht durch Quadrieren eines Fehlers $10^{{-m}}$ eine Fehlerabschätzung proportional zu $10^{{-2m}}$ . Deshalb spricht man davon, dass sich die Anzahl der gültigen Stellen in jedem Schritt der Newtoniteration ungefähr verdoppelt.

Konvergenzbetrachtungen

Das Newtonverfahren für das Polynom $z^{3}-1$ über den komplexen Zahlen konvergiert für Startwerte aus den roten, den grünen und den blauen Bereichen jeweils zu einer der drei Nullstellen des Polynoms. Für Startwerte aus der hellen Struktur, dem Newtonfraktal, konvergiert das Verfahren nicht.

Das Newtonverfahren ist ein sogenanntes lokal konvergentes Verfahren. Konvergenz der in der Newtoniteration erzeugten Folge zu einer Nullstelle ist also nur garantiert, wenn der Startwert, d.h. das 0-te Glied der Folge, schon „ausreichend nahe“ an der Nullstelle liegt. Ist der Startwert zu weit entfernt, ist das Konvergenzverhalten nicht festgelegt, das heißt, es ist sowohl eine Divergenz der Folge möglich als auch eine Oszillation (bei der sich endlich viele Funktionswerte abwechseln) oder eine Konvergenz gegen eine andere Nullstelle der betrachteten Funktion.

Dynamik des Newtonverfahrens für die Funktion $x^{3}-2x+2$ mit Startwerten zwischen −4 und 4: Jede farbcodierte Zeile zeigt das Resultat eines Schritts des Verfahrens, angewandt auf die jeweils darüberliegende Zeile. Die Startwerte befinden sich in der obersten Zeile. Viele Startwerte konvergieren gegen die (einzige reellwertige) Nullstelle des Polynoms bei ca. −1,769, deren Farbe Mittelblau ist. Es gibt jedoch auch viele Startwerte, für welche das Verfahren nicht konvergiert und zwischen null (schwarz) und eins (rot) hin- und herpendelt. Die Menge dieser nicht zur Nullstelle führenden Startwerte enthält offene Intervalle, ist also eine Menge von positivem Maß und damit insbesondere keine Nullmenge.

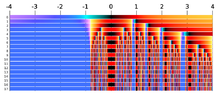
Ist der Startwert $x_{0}$ so gewählt, dass das Newtonverfahren konvergiert, so ist die Konvergenz allerdings quadratisch, also mit der Konvergenzordnung 2 (falls die Ableitung an der Nullstelle nicht verschwindet). Die Menge der Startpunkte, für die das Newtonverfahren gegen eine bestimmte Nullstelle konvergiert, bildet den Einzugsbereich dieser Nullstelle. Färbt man für eine Polynomfunktion, mit reellen oder komplexen Koeffizienten, die Einzugsbereiche verschiedener Nullstellen in der komplexen Ebene unterschiedlich ein, so ergibt sich ein Newtonfraktal. In diesem ist zu erkennen, dass die Einzugsbereiche Bassins, d.h. Kreisscheiben um die Nullstellen enthalten, aus welchen heraus die Newtoniteration stabil gegen die Nullstelle im Zentrum konvergiert. Aber es ist auch zu erkennen, dass die Ränder der Einzugsbereiche „ausgefranst“ sind, sie haben sogar eine fraktale Struktur. Geringe Abweichungen im Startpunkt können also zu unterschiedlichen Nullstellen führen.

Falls es jedoch im Intervall $I={]a,b[}$ genau eine Nullstelle gibt, in durchweg $f'>0$ sowie $f''<0$ gilt und der Startwert $x_{0}\in I$ links von der Nullstelle $\xi \in I$ gewählt wird, dann konvergiert die Folge im Newtonverfahren stets, und zwar streng monoton wachsend (siehe Abbildung unten bzw. die Tabelle oben ab n=1 ).

Beispiele für Nicht-Konvergenz

Oszillierendes Verhalten ergibt sich u.a. für das Polynom $f(x):=x^{3}-2x+2$ mit $f^{\prime }(x)=3x^{2}-2$ . Der Punkt mit und $f^{\prime }(0)=-2$ wird durch den Newtonoperator auf den Punkt abgebildet, der Punkt wiederum, mit und $f^{\prime }(1)=1$ , wird auf abgebildet, so dass die Newtoniteration mit einem dieser Punkte als Startwert eine periodische Folge ergibt, diese beiden Punkte wechseln sich zyklisch ab. Dieser Zyklus ist stabil, er bildet einen Attraktor der Newtoniteration. Das bedeutet, um beide Punkte gibt es Umgebungen, so dass Startpunkte aus diesen Umgebungen gegen den Zyklus konvergieren und somit je einen der Punkte 0 und 1 als Grenzwert der Teilfolge mit geradem Index und der mit ungeradem Index haben.
Divergenz bzw. beliebig weites Entfernen vom Startpunkt ergibt sich für $f(x)=\sin(x)$ mit $f^{\prime }(x)=\cos(x)$ und $N(x)=x-\tan(x)$ . Es gibt eine Stelle $x_{0}\in \lbrack -\pi /2,0\rbrack$ mit $\tan(x_{0})=-2\pi$ d.h. $x_{0}=\arctan(-2\pi )=-1{,}412965136506737759\dots$ Man überzeugt sich, dass dann $x_{n}=x_{0}+2\pi n$ gilt. Dieses Verhalten ist nicht stabil, denn bei leichter Variation des Anfangswertes, wie sie zum Beispiel durch die numerische Berechnung entsteht, entfernt sich die Newtoniteration immer weiter von der idealen divergierenden Folge. Selbst bei schließlicher Konvergenz wird die gefundene Nullstelle sehr weit vom Startwert entfernt sein.

Lokale quadratische Konvergenz

Sei eine zweimal stetig differenzierbare reelle Funktion und eine einfache Nullstelle von , in welcher die Ableitung somit keine Nullstelle hat. Das bedeutet, dass der Graph der Funktion transversal, d.h. nicht-berührend, die -Achse schneidet. Sei ein Punkt nahe bei . Dann kann die Taylorformel zweiten Grades (mit Lagrange-Restglied)

$0=f(a)=f(x)+f'(x)(a-x)+{\tfrac {1}{2}}f''(\xi )(a-x)^{2},\qquad \xi$ liegt zwischen und ,

nach der Differenz (x-a) umgestellt werden,

$x-a={\frac {f(x)}{f'(x)}}+{\frac {f''(\xi )}{2\,f'(x)}}(x-a)^{2}$ .

Es wird nun so umgestellt, dass der Newtonoperator auf der rechten Seite erscheint,

$N_{f}(x)-a=x-{\frac {f(x)}{f'(x)}}-a={\frac {f''(\xi )}{2\,f'(x)}}(x-a)^{2}$ .

Seien ein Intervall um ohne Nullstelle der Ableitung f'(x) und $m_{1}=\min _{x\in I}|f'(x)|$ sowie $M_{2}=\max _{x\in I}|f''(x)|$ Schranken der Ableitungen von . Dann folgt für alle $x\in I$ die Abschätzung

${\Bigl |}N_{f}(x)-a{\Bigr |}\leq {\frac {M_{2}}{2m_{1}}}|x-a|^{2}$ .

Mit $K={\tfrac {M_{2}}{2m_{1}}}$ sei der konstante Faktor bezeichnet. In jedem Schritt der Newtoniteration wird die Größe $d_{n}=K\,|x_{n}-a|$ kleiner sein als das Quadrat derselben Größe im vorhergehenden Schritt, $d_{n}\leq K\cdot K|x_{n-1}-a|^{2}=d_{n-1}^{2}$ . Nach vollständiger Induktion ergibt sich

$K\,|x_{n}-a|=d_{n}\leq d_{n-1}^{2}\leq d_{n-2}^{4}\leq \dotsb \leq d_{0}^{2^{n}}=(K\,|x_{0}-a|)^{2^{n}}$ .

Kann also für den Startpunkt der Iteration die Abschätzung $|x_{0}-a|<{\tfrac {1}{K}}$ garantiert werden, z.B. indem die Intervalllänge von kleiner als 1/K ist, so konvergiert die Folge $(x_{n})$ der Newtoniteration gegen die Nullstelle , denn die Folge $(d_{n})_{n\in \mathbb {N} }$ und damit $(x_{n}={\tfrac {1}{K}}d_{n})_{n\in \mathbb {N} }$ ist nach der angegebenen Abschätzung eine Nullfolge. Die Verkürzung des Intervalls kann durch einige Iterationen eines langsameren Verfahrens zur Nullstelleneinschränkung erreicht werden, z.B. des Bisektionsverfahrens oder der Regula falsi.

Die aus dieser Abschätzungen folgende Konvergenzgeschwindigkeit wird als quadratisch bezeichnet, die (logarithmische) Genauigkeit bzw. Anzahl gültiger Stellen verdoppelt sich in jedem Schritt. Die Abschätzung des Abstands $|x_{n}-a|$ zur Nullstelle wird oft linear in $|x_{0}-a|$ angegeben, so gilt z.B.

$|x_{n}-a|\leq \left({\tfrac {1}{2}}\right)^{2^{n}-1}\cdot |x_{0}-a|$ , falls die Länge des Intervalls kleiner als ${\tfrac {1}{2K}}$ ist. Dies ergibt eine Abschätzung der gültigen Stellen im Binärsystem.
$|x_{n}-a|\leq \left({\tfrac {1}{10}}\right)^{2^{n}-1}\cdot |x_{0}-a|$ , falls die Länge des Intervalls kleiner als ${\tfrac {1}{10K}}$ ist, d.h. nahe genug an der Nullstelle ergibt sich eine Verdopplung der gültigen Dezimalstellen in jedem Schritt.

Lokale quadratische Konvergenz bei mehrfacher Nullstelle durch Modifikation

Für den Fall, dass bei eine mehrfache Nullstelle endlichen Grades besitzt, lässt sich ebenfalls die Konvergenzgeschwindigkeit abschätzen und durch eine geringfügige Modifikation wieder quadratische Konvergenz erzwingen.

Hat bei eine -fache Nullstelle, lässt sich schreiben als $f(x)=(x-a)^{k}\cdot g(x)$ mit $g(a)\neq 0$ .

Dann ist nach der Produktregel $f'(x)=k\cdot (x-a)^{k-1}\cdot g(x)+(x-a)^{k}\cdot g'(x)$ und damit der Ausdruck

${\frac {f(x)}{f'(x)}}={\frac {(x-a)^{k}\cdot g(x)}{k\cdot (x-a)^{k-1}\cdot g(x)+(x-a)^{k}\cdot g'(x)}}=(x-a){\frac {g(x)}{k\cdot g(x)+(x-a)\cdot g'(x)}}$ .

Setzt man dies nun in die Iteration ein, so erhält man

$x_{\text{neu}}=x-{\frac {f(x)}{f'(x)}}=x-(x-a){\frac {g(x)}{k\cdot g(x)+(x-a)\cdot g'(x)}}$

und daraus nach beidseitiger Subtraktion von den Iterationsfehler

$(x_{\text{neu}}-a)=(x-a)-(x-a){\frac {g(x)}{k\cdot g(x)+(x-a)\cdot g'(x)}}=(x-a)\left[1-{\frac {g(x)}{k\cdot g(x)+(x-a)\cdot g'(x)}}\right]$ . (*)

Wenn nun der Ausdruck (x-a) sehr klein geworden ist, wird der Summand $(x-a)\cdot g'(x)$ im Nenner viel kleiner als $k\cdot g(x)$ , so dass sich die hintere Klammer in (*) immer mehr dem Wert $s=1-{\tfrac {1}{k}}$ nähert. Für die einfache Nullstelle mit k=1 hat man einen kleinen Wert , der fast 0 wird, so dass $(x_{\text{neu}}-a)=(x-a)\cdot s$ wird. Für k=2 wird ungefähr 0,5, so dass sich der Abstand zur Nullstelle von Schritt zu Schritt nur etwa halbiert und man nach etwa 10 Schritten die Genauigkeit nur in weiteren drei Dezimalstellen erhöht hat. Bei k=3 wird etwa 0,67, so dass erst nach etwa 16 Schritten die Genauigkeit um weitere drei Dezimalstellen steigt usw.

Man kann daher am Konvergenzverhalten die Vielfachheit der Nullstelle abschätzen, falls man sie nicht aus anderen Gründen weiß, und – wie nun noch beschrieben – das Verfahren optimieren.

Bei einer -fachen Nullstelle modifiziert man das newtonsche Näherungsverfahren mit einem Faktor :

$x_{\text{neu}}=x-k\cdot {\frac {f(x)}{f'(x)}}$ (Newtonverfahren bei -facher Nullstelle)

Damit wird dann (*) zu

${\begin{aligned}(x_{\text{neu}}-a)&=(x-a)\left[1-{\frac {k\cdot g(x)}{k\cdot g(x)+(x-a)\cdot g'(x)}}\right]\\&=(x-a)\left[{\frac {k\cdot g(x)+(x-a)\cdot g'(x)}{k\cdot g(x)+(x-a)\cdot g'(x)}}-{\frac {k\cdot g(x)}{k\cdot g(x)+(x-a)\cdot g'(x)}}\right]\\&=(x-a){\frac {(x-a)\cdot g'(x)}{k\cdot g(x)+(x-a)\cdot g'(x)}}\\&=(x-a)^{2}{\frac {g'(x)}{k\cdot g(x)+(x-a)\cdot g'(x)}}\end{aligned}}$

Ist nun (x-a) wieder sehr klein, so wird im Nenner der Summand $(x-a)\cdot g'(x)$ viel kleiner als $k\cdot g(x)$ , und man erhält

$(x_{\text{neu}}-a)=(x-a)^{2}{\frac {g'(x)}{k\cdot g(x)}}$ ,

wobei der rechte Faktor wegen $g(a)\neq 0$ gegen einen festen Wert konvergiert. Wie man sieht, liegt nun auch hier quadratische Konvergenz vor.

Ein Beispiel zeigt das Konvergenzverhalten sehr schön. Die Funktion $f(x)=x^{2}-2$ hat die einfache Nullstelle ${\sqrt {2}}$ . Die linke Spalte der Tabelle zeigt die rasche Konvergenz für den Startwert 1, nach 4 Schritten lässt sich die Genauigkeit nicht mehr steigern, beim Fehler verdoppelt sich die Anzahl der Nullen hinterm Komma (mindestens). Quadriert man nun die Funktion (mittlere Spalte), wird die Nullstelle eine doppelte, und nun zeigt sich das oben erläuterte Verhalten, dass sich ohne Modifikation der Fehler in jedem Schritt nur etwa halbiert. Modifiziert man dann diesen Fall mit dem Faktor k=2 , so stellt sich dasselbe Verhalten wie bei der einfachen Nullstelle ein (rechte Spalte).

n	$x_{n}$ für $f(x)=x^{2}-2$	Fehler	$x_{n}$ für $f(x)=(x^{2}-2)^{2}$ ohne Faktor	Fehler	$x_{n}$ für $f(x)=(x^{2}-2)^{2}$ mit Faktor	Fehler
0
1
2
3
4		$0$				$0$
5		$0$				$0$
6		$0$				$0$
7		$0$				$0$
8		$0$				$0$
9		$0$				$0$
10		$0$				$0$

Das Newtonverfahren für komplexe Zahlen

Für komplexe Zahlen schreibt man die Formel entsprechend:

$(1)\,z_{1}=z_{0}-{\frac {f(z_{0})}{f\,'\,(z_{0})}}$

mit der holomorphen Funktion $f(z),\,z=x+iy,\,i^{2}=-1,\;x,y\in \mathbb {R}$ . Die Zerlegung in Real- und Imaginärteil ergibt

$f(z)=u(x,y)+iv(x,y)$

Die komplexe Ableitung ist unabhängig von der Richtung der Ableitung an der Stelle d.h. es gilt

${\frac {d}{dz}}f(z)\;=\;{\frac {\partial }{\partial x}}f(z)\;=\;{\frac {\partial }{\partial \,(iy)}}f(z)\;=\;{\frac {\partial }{i\,\partial \,y}}\,f(z)$

Daher gelten die Cauchy-Riemann'schen Differentialgleichungen

$(2)\,u_{x}=v_{y}$ und $v_{x}=-u_{y}.$

Die komplexe Gleichung (1) kann in Real- und Imaginärteil zerlegt werden:

$(3)\,{\frac {f(z)}{f\,'(z)}}\,=\,{\frac {f(z)\cdot {\overline {\,f\,'(z)}}}{f\,'(z)\,\cdot {\overline {f\,'(z)}}}}\,=\,{\frac {(u+iv)\cdot (u_{x}-iv_{x})}{u_{x}^{2}+v_{x}^{2}}}$ .

Mit Hilfe (2) folgt hieraus

${\frac {f(z)}{f\,'(z)}}\,={\frac {1}{u_{x}^{2}+v_{x}^{2}}}\cdot \left\{\left(u\cdot u_{x}+v\cdot v_{x}\right)+i\left(u\cdot u_{y}+v\cdot v_{y}\right)\right\}$

Die geometrische Bedeutung dieser Gleichung sieht man wie folgt. Man bestimmt das Minimum vom Betrag $\vert f(z)\vert$ . Das Minimum wird für $f(z)=0$ angenommen. Dies kann mit dem Gradientenverfahren, d.h. mit der Methode des steilsten Abstiegs bestimmt werden.

Man führt die Bezeichnung $b(x,y)=\vert f(z)\vert ={\sqrt {u^{2}\,+\,v^{2}}}$ ein. Die Formel für diese Methode lautet mit dem Vektor ${\vec {x}}\,=\left({\begin{array}{*{20}c}{x}\\{y}\\\end{array}}\right)$ :

$(4)\,{\vec {x}}_{1}\;=\;{\vec {x}}_{0}\;-\;{\frac {b(x_{0},y_{0})}{\left|\,-\nabla \,b(x_{0},y_{0})\right|^{2}}}\cdot -\nabla \,b(x_{0},y_{0}).$

Dies ist mit der Formel (1) identisch.

Bemerkungen

Der lokale Konvergenzbeweis kann auch auf die gleiche Weise im mehrdimensionalen Fall geführt werden, allerdings ist er dann technisch etwas schwieriger, da mit zwei- und dreistufigen Tensoren für die erste bzw. zweite Ableitung gearbeitet wird. Im Wesentlichen ist die Konstante K durch $K={\tfrac {1}{2}}\,\sup _{x\in U}\|f'(x)^{-1}\|_{(1,1)}\,\sup _{x\in U}\|f''(x)\|_{(1,2)}$ zu ersetzen, mit geeigneten induzierten Operatornormen.
Der lokale Konvergenzbeweis setzt voraus, dass ein eine Nullstelle enthaltendes Intervall bekannt ist. Aus seinem Beweis ergibt sich aber keine Möglichkeit, dies schnell zu testen. Ein Konvergenzbeweis, der auch hierfür ein Kriterium liefert, wurde zuerst von Leonid Kantorowitsch geführt und ist als Satz von Kantorowitsch bekannt.
Um einen geeigneten Startpunkt zu finden, verwendet man gelegentlich andere („gröbere“) Verfahren. Beispielsweise kann man mit dem Gradientenverfahren eine ungefähre Lösung ermitteln und diese dann mit dem Newtonverfahren verfeinern.
Bei unbekanntem Startpunkt kann man mittels einer Homotopie die Funktion , von der man eine Nullstelle sucht, zu einer einfacheren Funktion deformieren, von der (mindestens) eine Nullstelle bekannt ist. Man durchläuft dann die Deformation rückwärts in Form einer endlichen Folge sich nur „wenig“ unterscheidender Funktionen. Von der ersten Funktion kennt man eine Nullstelle. Als Startwert der Newtoniteration zur gerade aktuellen Funktion der Folge verwendet man die Näherung einer Nullstelle der in der Folge vorhergehenden Funktion. Zum genauen Vorgehen siehe Homotopieverfahren.

Als Beispiel mag die „Flutungshomotopie“ dienen: mit einem willkürlichen bilden wir die Ausgangsfunktion $g(x)=f_{0}(x):=f(x)-f(z)$ mit bekannter Nullstelle . Wir haben den „Wasserspiegel“ vom „Nullpegel“ auf die Höhe f(z)

geflutet. Nun senken wir schrittweise den Wasserstand, $f_{n}(x):=f(x)-(f(z)-n\cdot h\cdot f(z))$ , h=1/N

, $n=1\dots N$ . In jedem Schritt wird eine Näherung $\xi ^{(n)}$ einer Nullstelle bestimmt, wobei $x_{0}:=\xi ^{(n-1)}$ gesetzt wird. Es ist $f_{N}=f$ und somit $\xi ^{(N)}$ eine der gesuchten Näherungslösungen.

Das newtonsche Näherungsverfahren

Abbruchkriterien

Mögliche Abbruchkriterien bezüglich einer Restgröße (zum Beispiel Rechner-Arithmetik) sind:

$\|f(x_{n})\|<\varepsilon _{1}\qquad \mathrm {oder} \qquad \|x_{n+1}-x_{n}\|<\varepsilon _{2}$

Wobei $\varepsilon _{1},\varepsilon _{2}\in \mathbb {R} ^{+}$ die Qualität der „Nullstelle“ bestimmt. In beiden Fällen kann es vorkommen, dass das Abbruchkriterium zu einem „schlechten“ Zeitpunkt erfüllt ist.

Weitere Anwendungsbeispiele

Lösen eines Optimierungsproblems

Das Newtonverfahren kann verwendet werden, um einen Extremwert einer Funktion $f\colon \mathbb {R} \to \mathbb {R}$ zu finden. Dafür sucht man mit dem Verfahren nach einem Kritischen Punkt, d.h. nach einer Nullstelle in der ersten Ableitung der Funktion. Der Iterationsschritt sieht demnach wie folgt aus:

$x_{n+1}=x_{n}-{\frac {f'(x_{n})}{f''(x_{n})}}$

Für eine Funktion $f\colon \mathbb {R} ^{n}\to \mathbb {R}$ mit mehreren Eingangsvariablen $\mathbf {x} \in \mathbb {R} ^{n}$ verwendet man analog die Jacobimatrix $J\in \mathbb {R} ^{n\times 1}$ und die inverse Hessematrix $H\in \mathbb {R} ^{n\times n}$ (siehe auch Das Newtonverfahren im Mehrdimensionalen):

$\mathbf {x} _{n+1}=\mathbf {x} _{n}-H(\mathbf {x} _{n})^{-1}J(\mathbf {x} _{n})$

Berechnung der Quadratwurzel

Ein Spezialfall des newtonschen Näherungsverfahrens ist das babylonische Wurzelziehen, auch bekannt als Heronverfahren nach Heron von Alexandria:

Wendet man die Iterationsformel zur Nullstellenbestimmung auf die Funktion

$f(x)=x^{2}-a$

an, so erhält man wegen der Ableitungsfunktion f'(x)=2x für die Lösung ${\sqrt {a}}$ das Näherungsverfahren

$x_{n+1}:=x_{n}-{\frac {x_{n}^{2}-a}{2x_{n}}}={\frac {2x_{n}^{2}-x_{n}^{2}+a}{2x_{n}}}={\frac {1}{2}}\left(x_{n}+{\frac {a}{x_{n}}}\right)$ .

Dieses Verfahren konvergiert für jedes $a\geq 0$ und für jeden beliebigen Anfangswert $x_{0}\neq 0$ .

Berechnung der Kubikwurzel

Wendet man die Iterationsformel zur Nullstellenbestimmung auf die Funktion

$f(x)=x^{3}-a$

an, so erhält man wegen der Ableitungsfunktion $f'(x)=3x^{2}$ für die Lösung ${\sqrt[{3}]{a}}$ das Näherungsverfahren

$x_{n+1}:=x_{n}-{\frac {x_{n}^{3}-a}{3x_{n}^{2}}}=x_{n}-{\frac {1}{3}}\left(x_{n}-{\frac {a}{x_{n}^{2}}}\right)={\frac {1}{3}}\left(2x_{n}+{\frac {a}{x_{n}^{2}}}\right)$ .

Für negative Radikanden empfiehlt sich die Umrechnung mit ${\sqrt[{3}]{x}}=-{\sqrt[{3}]{-x}}$ .

Dieses Verfahren konvergiert für und Anfangswert $x_{0}\neq 0$ , wenn und $x_{0}$ gleiches Vorzeichen haben.

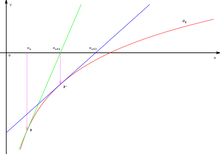
Schnittpunkt zweier Funktionen

Auf ähnliche Weise lässt sich auch der -Wert des Schnittpunktes zweier Funktionen g(x) und f(x) bestimmen:

Da man die beiden Funktionen zur Lösung des Problems gleichsetzt, lässt sich immer durch Umformung folgende Form, auf die das newtonsche Näherungsverfahren angewendet werden kann, bestimmen:

Gemischt-goniometrische Funktion

Gesucht sei die positive Lösung der Gleichung $\cos(x)=x^{3}$ . Das Problem kann umformuliert werden als $\cos(x)-x^{3}=0$ . Gesucht werden also Nullstellen von $f(x)=\cos(x)-x^{3}$ .

Wir haben nun $f'(x)=-\sin(x)-3x^{2}$ . Da $\cos(x)\leq 1$ für alle gilt und $x^{3}>1$ für x>1 , wissen wir, dass die Nullstelle zwischen 0 und 1 liegt. Wir starten die Iteration mit dem Wert $x_{0}=0{,}5$ .

${\begin{matrix}x_{1}&=&x_{0}-{\frac {f(x_{0})}{f'(x_{0})}}&=&0{,}5-{\frac {\cos(0{,}5)-0{,}5^{3}}{-\sin(0{,}5)-3\cdot 0{,}5^{2}}}&\approx &1{,}11214163710\\x_{2}&=&x_{1}-{\frac {f(x_{1})}{f'(x_{1})}}&&\vdots &\approx &0{,}909672693736\\x_{3}&&\vdots &&\vdots &\approx &0{,}867263818209\\x_{4}&&\vdots &&\vdots &\approx &0{,}865477135298\\x_{5}&&\vdots &&\vdots &\approx &0{,}865474033111\\x_{6}&&\vdots &&\vdots &\approx &0{,}865474033101\\x_{7}&&\vdots &&\vdots &\approx &0{,}865474033102\end{matrix}}$

Damit sind die ersten zwölf Ziffern der Nullstelle bekannt.

Das Newton-Verfahren im Mehrdimensionalen

Das Newtonverfahren kann auch benutzt werden, um Nullstellen von mehrdimensionalen Funktionen $f\colon \mathbb {R} ^{n}\to \mathbb {R} ^{n}$ zu bestimmen. Ein konkreter Anwendungsfall ist die Kombination mit der Gaußschen Fehlerquadratmethode im Gauß-Newton-Verfahren. Für den allgemeinen Fall ist der Ausgangspunkt eine Taylorentwicklung der Funktion :

${\begin{aligned}f(\mathbf {x} +\mathbf {h} )=f(\mathbf {x} )+J(\mathbf {x} )\cdot \mathbf {h} +{\mathcal {O}}(\|\mathbf {h} \|^{2}),\quad {\text{für}}\quad \mathbf {x} ,\mathbf {h} \in \mathbb {R} ^{n}\end{aligned}}$

wobei $J(\mathbf {x} )=f'(\mathbf {x} )={\frac {\partial f}{\partial \mathbf {x} }}(\mathbf {x} )$ die Jacobimatrix, also die Matrix der partiellen Ableitungen von $f(\mathbf {x} )\,$ , ist:

$J(\mathbf {x} ):=\left({\frac {\partial f_{i}}{\partial x_{j}}}(\mathbf {x} )\right)_{ij}={\begin{pmatrix}{\frac {\partial f_{1}}{\partial x_{1}}}&{\frac {\partial f_{1}}{\partial x_{2}}}&\ldots &{\frac {\partial f_{1}}{\partial x_{n}}}\\{\frac {\partial f_{2}}{\partial x_{1}}}&{\frac {\partial f_{2}}{\partial x_{2}}}&\ldots &{\frac {\partial f_{2}}{\partial x_{n}}}\\\vdots &\vdots &\ddots &\vdots \\{\frac {\partial f_{n}}{\partial x_{1}}}&{\frac {\partial f_{n}}{\partial x_{2}}}&\ldots &{\frac {\partial f_{n}}{\partial x_{n}}}\end{pmatrix}}.$

Anstatt nach Nullstellen der nicht-linearen Funktion zu suchen, sucht man nach Nullstellen der linearen Anpassung von im Punkt $\mathbf {x}$ :

${\tilde {f}}(\mathbf {h} ):=f(\mathbf {x} )+J(\mathbf {x} )\cdot \mathbf {h} {\overset {!}{=}}0.$

Für $\mathbf {x} =\mathbf {x_{n}}$ und $\mathbf {h} =\mathbf {x_{n+1}} -\mathbf {x_{n}}$ inspiriert dies das Newtonverfahren:

$\mathbf {x} _{n+1}:=N_{f}(\mathbf {x} _{n})=\mathbf {x} _{n}-(J(\mathbf {x} _{n}))^{-1}f(\mathbf {x} _{n}).$

Da das Lösen von

$\Delta \mathbf {x} _{n}:=-(J(\mathbf {x} _{n}))^{-1}f(\mathbf {x} _{n})\;,$

über die Berechnung der Inversen einer Matrix und anschließender Multiplikation mit $f(\mathbf {x} _{n})$ aufwendiger und numerisch ungünstiger ist, wird stattdessen das lineare Gleichungssystem

$J(\mathbf {x} _{n})\;\Delta \mathbf {x} _{n}=-f(\mathbf {x} _{n})$

gelöst. Danach erhält man $\mathbf {x} _{n+1}$ aus:

$\mathbf {x} _{n+1}=\mathbf {x} _{n}+\Delta \mathbf {x} _{n}.$

Zum Lösen des Systems existieren verschiedene Lösungsverfahren. Ist die Jacobimatrix in der Nullstelle invertierbar und in einer Umgebung der Nullstelle lipschitzstetig, so konvergiert das Verfahren lokal quadratisch.

Varianten des Newtonverfahrens

Das größte Problem bei der Anwendung des Newtonverfahrens liegt darin, dass man die erste Ableitung der Funktion benötigt. Deren Berechnung ist meist aufwendig, und in vielen Anwendungen ist eine Funktion auch nicht analytisch gegeben, sondern beispielsweise nur durch ein Computerprogramm. Im Eindimensionalen ist dann die Regula falsi vorzuziehen, bei der die Sekante und nicht die Tangente benutzt wird. Im Mehrdimensionalen muss man andere Alternativen suchen. Hier ist das Problem auch dramatischer, da die Ableitung eine Matrix mit $n^{2}$ Einträgen ist, der Aufwand der Berechnung steigt also quadratisch mit der Dimension.

Vereinfachtes Newtonverfahren

Statt die Ableitung in jedem Newton-Schritt auszurechnen, ist es auch möglich, sie nur in jedem n-ten Schritt zu berechnen. Dies senkt die Kosten für einen Iterationsschritt drastisch, der Preis ist ein Verlust an Konvergenzgeschwindigkeit. Die Konvergenz ist dann nicht mehr quadratisch, es kann aber weiterhin superlineare Konvergenz erreicht werden.

Inexaktes Newtonverfahren

Eine ähnliche Idee besteht darin, in jedem Schritt eine Approximation der Ableitung zu berechnen, beispielsweise über finite Differenzen. Eine quantitative Konvergenzaussage ist in diesem Fall schwierig, als Faustregel lässt sich jedoch sagen, dass, je schlechter die Approximation der Ableitung ist, desto schlechter die Konvergenz wird. Ein Beispiel für ein solches Verfahren ist das Sekantenverfahren.

Newton-Krylow-Verfahren

Für die numerische Lösung nichtlinearer partieller Differentialgleichungen bietet sich prinzipiell das Newtonverfahren als Grundlöser an. Die entsprechende Jacobimatrix ist immer dünnbesetzt, und daher bieten sich Krylow-Unterraum-Verfahren zur Lösung der linearen Gleichungssysteme an. Man spricht dann von Newton-Krylow-Verfahren. Im Krylowverfahren selbst tritt die Jacobimatrix nur in Matrix-Vektorprodukten auf, welche als Richtungsableitungen interpretiert werden können. Approximiert man diese durch finite Differenzen, so erhält man matrixfreie Verfahren.

Literatur

P. Deuflhard, A. Hohmann: Numerische Mathematik I. Eine algorithmisch orientierte Einführung. 3. überarbeitete und erweiterte Auflage. De Gruyter, Berlin, New York 2002, ISBN 3-11-017182-1.
M. Hermann: Numerische Mathematik, Band 1: Algebraische Probleme. 4., überarbeitete und erweiterte Auflage. Walter de Gruyter Verlag, Berlin und Boston 2020, ISBN 978-3-11-065665-7.

Basierend auf einem Artikel in:

Wikipedia.de