Gradientenverfahren

Das Gradientenverfahren wird in der Numerik eingesetzt, um allgemeine Optimierungsprobleme zu lösen. Dabei schreitet man (am Beispiel eines Minimierungsproblems) von einem Startpunkt aus entlang einer Abstiegsrichtung, bis keine numerische Verbesserung mehr erzielt wird. Wählt man als Abstiegsrichtung den negativen Gradient, also die Richtung des lokal steilsten Abstiegs, erhält man das Verfahren des steilsten Abstiegs. Manchmal werden die Begriffe Gradientenverfahren und Verfahren des steilsten Abstiegs synonym verwendet. Im Allgemeinen bezeichnet Gradientenverfahren eine Optimierungsmethode, bei der die Abstiegsrichtung durch Gradienteninformation gewonnen wird, also nicht notwendigerweise auf den negativen Gradient beschränkt ist.

Das Verfahren des steilsten Abstiegs konvergiert oftmals sehr langsam, da es sich dem stationären Punkt mit einem starken Zickzack-Kurs nähert. Andere Verfahren für die Berechnung der Abstiegsrichtung erreichen teils deutlich bessere Konvergenzgeschwindigkeiten, so bietet sich für die Lösung von symmetrisch positiv definiten linearen Gleichungssystemen beispielsweise das Verfahren der konjugierten Gradienten an. Der Gradientenabstieg ist mit dem Bergsteigeralgorithmus (hill climbing) verwandt.

Das Optimierungsproblem

Das Gradientenverfahren ist einsetzbar, um eine reellwertige, differenzierbare Funktion $f\colon \mathbb {R} ^{n}\rightarrow \mathbb {R}$ zu minimieren:

${\underset {x\in \mathbb {R} ^{n}}{\min }}\ f(x).$

Hierbei handelt es sich um ein Problem der Optimierung ohne Nebenbedingungen, auch unrestringiertes Optimierungsproblem genannt.

Das Verfahren

Das Gradientenverfahren generiert ausgehend von einem Startpunkt $x^{0}\in \mathbb {R} ^{n}$ eine Folge von Punkten $x^{k}\in \mathbb {R} ^{n}$ gemäß der Iterationsvorschrift

$x^{k+1}=x^{k}+\alpha ^{k}d^{k},\quad k=0,1,\ldots$

wobei $\alpha ^{k}>0$ eine positive Schrittweite ist und $d^{k}\in \mathbb {R} ^{n}$ eine Abstiegsrichtung. Dabei werden sowohl $\alpha^k$ als auch $d^{k}$ in jedem Iterationsschritt so bestimmt, dass die Folge x^k zu einem stationären Punkt von konvergiert.

Bestimmen der Abstiegsrichtung

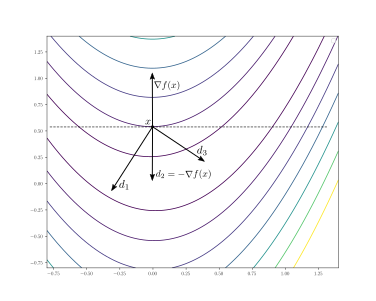
Abstiegsrichtungen $d_{i}$ haben einen Winkel größer als 90° mit dem Gradienten im Punkt . Die strichlierte Gerade ist die Tangente an die Isolinie der zweidimensionalen Funktion, sie stellt den Grenzfall dar bei dem der Winkel mit dem Gradient 90° beträgt. Die Abstiegsrichtung $d_{2}$ zeigt in Richtung des negativen Gradienten, d.h. in Richtung des steilsten Abstiegs.

Eine Abstiegsrichtung im Punkt x^k ist ein Vektor $d^{k}$ , der

$\left(\nabla f(x^{k})\right)^{T}d^{k}<0$

erfüllt. Intuitiv bedeutet das, dass der Winkel zwischen $\nabla f(x^{k})$ und $d^{k}$ größer als 90° ist. Da der Gradient $\nabla f(x^{k})$ in Richtung des steilsten Anstiegs zeigt, ist $d^{k}$ eine Richtung entlang derer sich der Funktionswert verringert.

Viele Gradientenmethoden berechnen die Abstiegsrichtung anhand

$d^{k}=-D^{k}\nabla f(x^{k}),$

wobei $D^{k}$ eine positiv definite Matrix ist. In diesem Fall lautet die Bedingung für die Abstiegsrichtung

$\left(\nabla f(x^{k})\right)^{T}\left(-D^{k}\right)\nabla f(x^{k})<0,$

und ist dank der positiven Definitheit von $D^{k}$ immer erfüllt.

Mit der Wahl der Matrix $D^{k}$ erhält man folgende Algorithmen:

$D^{k}=I$ , wobei die Einheitsmatrix ist, ergibt das Verfahren des steilsten Abstiegs. Die Absteigsrichtung ist in diesem Fall einfach der negative Gradient, $d^{k}=-\nabla f(x^{k})$ .
$D^{k}={\begin{bmatrix}a_{1}&0&\cdots &0\\0&a_{2}&\ddots &\vdots \\\vdots &\ddots &\ddots &0\\0&\cdots &0&a_{n}\end{bmatrix}}$ , wobei $a_{i}>0,\ i=1,\ldots ,n$ sodass $D^{k}$ positiv definit ist, ist ein diagonal skalierter steilster Abstieg. Oft werden die $a_{i}$ als Approximation der Inversen der 2. Ableitung gewählt, also $a_{i}\approx \left({\frac {\partial ^{2}f(x^{k})}{\left(\partial x_{i}\right)^{2}}}\right)^{-1}$ .
$D^{k}=\left(\nabla ^{2}f(x^{k})\right)^{-1}$ , die Inverse Hesse-Matrix, ergibt das Newton-Verfahren für die Lösung nichtlinearer Minimierungsprobleme.
Da die Berechnung der Hesse-Matrix oft aufwändig ist, gibt es eine Klasse von Algorithmen welche eine Approximation $D^{k}\approx \left(\nabla ^{2}f(x)\right)^{-1}$ verwenden. Solche Methoden werden als Quasi-Newton-Verfahren bezeichnet, es gibt verschiedene Arten wie die Approximation berechnet wird. Ein wichtiger Vertreter aus der Klasse der Quasi-Newton Methoden ist der BFGS Algorithmus.
Falls das Optimierungsproblem in der speziellen Form $\min _{x\in \mathbb {R} ^{n}}\left\{\|f(x)\|^{2}=\sum _{i=1}^{m}\left(f_{i}(x)\right)^{2}\right\}$ , also als Summe von Quadraten von Funktionen, gegeben ist, erhält man mit $D^{k}=\left(J^{T}J\right)^{-1}$ , wobei die Jacobi-Matrix von im Punkt ist, das Gauß-Newton-Verfahren.

Bestimmen der Schrittweite

Die Bestimmung der Schrittweite $\alpha^k$ ist ein wichtiger Teil des Gradientenverfahren, der großen Einfluss auf die Konvergenz haben kann. Ausgehend vom Iterationsschritt $x^{k+1}=x^{k}+\alpha ^{k}d^{k}$ betrachtet man den Wert von entlang der Linie $x^{k}+\alpha d^{k}$ , also $f(\alpha )=f(x^{k}+\alpha d^{k})$ . Man spricht in diesem Zusammenhang oft auch von Liniensuche. Die ideale Wahl wäre es, die Schrittweite als jenen Wert zu berechnen, der die Funktion $f(\alpha )$ minimiert, also das eindimensionale Problem

$\min _{\alpha >0}\left\{f(\alpha )=f(x^{k}+\alpha d^{k})\right\}$

zu lösen. Dies wird als exakte Liniensuche bezeichnet und wird in dieser Form in der Praxis selten angewandt, da selbst für einfache Optimierungsprobleme die exakte Bestimmung der Schrittweite sehr rechenaufwändig ist.

Als Alternative zur exakten Liniensuche lockert man die Erfordernisse und beschränkt sich darauf, dass der Funktionswert sich mit jedem Iterationsschritt „genügend“ verringert. Dies wird auch als inexakte Liniensuche bezeichnet. Die einfachste Möglichkeit besteht darin, die Schrittweite $\alpha$ ausgehend von einem Startwert (z.B. $\alpha =1$ ) so lange zu verringern, bis $f(x^{k+1})=f(x^{k}+\alpha d^{k})<f(x^{k})$ erreicht ist. Diese Methode funktioniert in der Praxis oft zufriedenstellend, man kann jedoch zeigen, dass für manche pathologischen Funktionen diese Liniensuche zwar in jedem Schritt den Funktionswert verringert, die Folge x^k jedoch nicht zu einem stationärem Punkt konvergiert.

Armijo-Bedingung

Die Armijo-Bedingung formalisiert das Konzept "genügend" in der geforderten Verringerung des Funktionswertes. Die Bedingung $f(x^{k}+\alpha d^{k})<f(x^{k})$ wird modifiziert zu

$f(x^{k}+\alpha d^{k})\leq f(x^{k})+\sigma \alpha \left(\nabla f(x^{k})\right)^{T}d^{k},$

mit $\sigma \in (0,1)$ . Die Armijo-Bedingung umgeht die Konvergenzprobleme aus der vorigen einfachen Bedingung, indem sie fordert dass die Verringerung zumindest proportional zur Schrittweite und zur Richtungsableitung $\left(\nabla f(x^{k})\right)^{T}d^{k}$ ist, mit Proportionalitätskonstante $\sigma$ . In der Praxis werden oft sehr kleine Werte verwendet, z.B. $\sigma =10^{-4}$ .

Backtracking Liniensuche

Die Armijo-Bedingung gilt immer dann, wenn die Schrittweite genügend klein ist und kann damit zum Stillstand des Gradientenverfahrens führen – der Schritt ist so klein, dass kein nennenswerter Fortschritt mehr gemacht wird. Eine einfache Kombination aus wiederholter Verkleinerung der Schrittweite und der Armijo-Bedingung ist die Backtracking-Liniensuche. Sie stellt sicher, dass die Schrittweite klein genug ist, um die Armijo-Bedingung zu erfüllen, andererseits aber nicht zu klein. In Pseudocode:

Wähle Startwert für , z.B. , wähle Konstanten

while 
  
end

Setze

Die Backtracking-Liniensuche verringert die Schrittweite wiederholt um den Faktor $\rho$ , bis die Armijo-Bedingung erfüllt ist. Sie terminiert garantiert nach einer endlichen Anzahl von Schritten und wird wegen ihrer Einfachheit oft in Praxis verwendet.

Konvergenz

Im Allgemeinen konvergiert das Gradientenverfahren weder zu einem globalen noch zu einem lokalen Minimum. Garantiert werden kann nur die Konvergenz zu einem stationären Punkt, also einem Punkt $x^{*}$ mit $\nabla f(x^{*})=0$ . Schränkt man die Klasse der Zielfunktionen auf konvexe Funktionen ein, so sind stärkere Garantien möglich, siehe konvexe Optimierung.

Konvergenzgeschwindigkeit

Für den allgemeinen Fall kann weder über die Konvergenzgeschwindigkeit der Folge $\{f(x^{k})\}$ noch über die Konvergenzgeschwindigkeit der Folge $\{x^{k}\}$ eine Aussage getroffen werden. Ist eine Lipschitz-Konstante von $\nabla f$ , so kann man zeigen, dass die Norm der Gradienten $g_{N}^{*}=\min _{0\leq k\leq N}\|\nabla f(x^{k})\|$ mit der Rate ${\sqrt {\frac {L\left(f(x^{0})-f(x^{*})\right)}{\omega (N+1)}}}$ gegen 0 konvergiert, wobei $\omega>0$ eine positive Konstante ist.

Beispiel

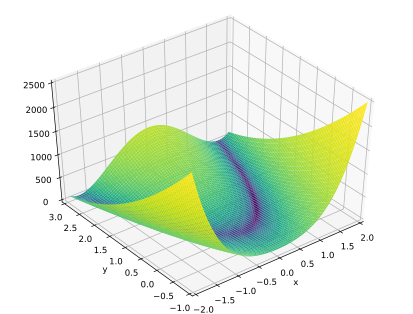
Die Rosenbrock Funktion mit $a=1,\ b=100$

Die Rosenbrock-Funktion

$f:\mathbb {R} ^{2}\to \mathbb {R} :x\mapsto \left(a-x_{1}\right)^{2}+b\left(x_{2}-x_{1}^{2}\right)^{2}$

wird häufig als Test für Optimierungsmethoden verwendet, da sie wegen des schmalen und flachen Tals, in welchem iterative Methoden nur kleine Schritte machen können, eine Herausforderung darstellt. Die Konstanten werden üblicherweise mit $a=1,\ b=100$ gewählt, das globale Optimum liegt in diesem Fall bei $x^{*}=(1,1)$ mit dem Funktionswert $f(x^{*})=0$ .

Der Gradient sowie die Hesse-Matrix ergeben sich als

$\nabla f={\begin{bmatrix}4bx_{1}^{3}-4bx_{1}x_{2}+2(x_{1}-a)\\2b(-x_{1}^{2}+x_{2})\end{bmatrix}}$

sowie

$\nabla ^{2}f={\begin{bmatrix}12bx_{1}^{2}-4bx_{2}+2&-4bx_{1}\\-4bx_{1}&2b\end{bmatrix}}$ .

Damit lassen sich die Algorithmen Verfahren des steilsten Abstiegs und Newton-Verfahren direkt implementieren. Um das Gauß-Newton-Verfahren anzuwenden, muss die Rosenbrock-Funktion zunächst in die Form „Summe von Quadraten von Funktionen“ gebracht werden. Dies ist auf der Seite zum Gauß-Newton-Verfahren im Detail erklärt.

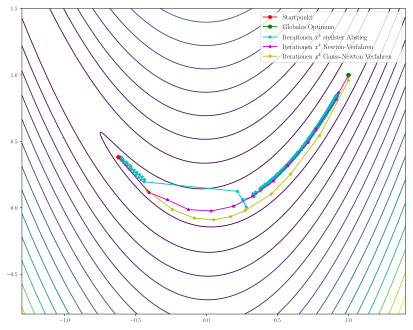
Optimierung mit Verfahren des steilsten Abstiegs, Newton-Verfahren und Gauß-Newton Verfahren

Für die Liniensuche kommt bei allen Verfahren ein Backtracking mit folgenden Parametern zum Einsatz: Startwert $\alpha =1$ , $\rho =0{,}5,\ \sigma =0{,}001$ . Als Startpunkt wird $x^{0}=(-0{,}62,-0{,}38)$ gewählt.

Das Verfahren des steilsten Abstiegs findet auch nach 1000 Iterationen nicht zum globalen Optimum und steckt in dem flachen Tal fest, wo nur sehr kleine Schritte möglich sind. Im Gegensatz dazu finden sowohl das Newton-Verfahren als auch der Gauß-Newton- Algorithmus in wenigen Iterationen zum globalen Optimum.

Siehe auch

Liniensuchverfahren

Basierend auf einem Artikel in:

Wikipedia.de