
Konvexe Optimierung
Die konvexe Optimierung ist ein Teilgebiet der mathematischen Optimierung.
Es ist eine bestimmte Größe zu minimieren, die sogenannte Zielfunktion, welche von
einem Parameter, welcher mit
bezeichnet wird, abhängt. Außerdem sind bestimmte Nebenbedingungen einzuhalten,
das heißt, die Werte
,
die man wählen darf, sind gewissen Einschränkungen unterworfen. Diese sind meist
in Form von Gleichungen und Ungleichungen gegeben. Sind für einen Wert
alle Nebenbedingungen eingehalten, so sagt man, dass
zulässig ist. Man spricht von einem konvexen Optimierungsproblem oder einem
konvexen Programm, falls sowohl die Zielfunktion als auch die Menge der
zulässigen Punkte konvex
ist. Viele Probleme der Praxis sind konvexer Natur. Oft wird zum Beispiel auf Quadern
optimiert, welche stets konvex sind, und als Zielfunktion finden oft quadratische Formen
wie in der quadratischen
Optimierung Verwendung, die unter bestimmten Voraussetzungen ebenfalls
konvex sind (siehe Definitheit).
Ein anderer wichtiger Spezialfall ist die Lineare
Optimierung, bei der eine lineare Zielfunktion über einem konvexen Polyeder optimiert wird.
Eine wichtige Eigenschaft der konvexen Optimierung im Unterschied zur nicht-konvexen Optimierung ist, dass jedes lokale Optimum auch ein globales Optimum ist. Anschaulich bedeutet dies, dass eine Lösung, die mindestens so gut ist wie alle anderen Lösungen in einer Umgebung, auch mindestens so gut ist wie alle zulässigen Lösungen. Dies erlaubt es, einfach nach lokalen Optima zu suchen.
Problemstellung
Es gibt viele mögliche Formulierungen eines konvexen Programms. Eines der am häufigsten verwendeten und mathematisch am leichtesten handhabbaren ist
Der Eingabeparameter
sei aus dem
,
das heißt, das Problem hängt von
Einflussparametern ab. Die Zielfunktion
sei konvex auf ihrem Definitionsbereich
,
genauso wie die Ungleichungsrestriktionen
.
Die
sind auf ganz
definierte affine
Funktionen der Form
.
Die Menge
heißt dann die Definitionsmenge des konvexen Programms. Sie ist die größte
Menge, auf der alle Funktionen definiert und konvex sind. Außerdem ist sie als
Schnitt konvexer Mengen auch konvex. Die Funktionen
stellen die sogenannten Ungleichungsnebenbedingungen und die Funktionen
stellen die sogenannten Gleichungsnebenbedingungen dar. Die Funktion
heißt die Zielfunktion und die Menge
die Restriktionsmenge des Problems. Sie ist eine konvexe Menge, da Subniveaumengen konvexer Funktionen wieder konvex sind.
Varianten
Konkave Zielfunktion
Meist werden auch Probleme der Form „Maximiere
unter konvexen Nebenbedingungen“ als konvexe Probleme bezeichnet, wenn
eine konkave Funktion ist. Dieses Problem ist äquivalent (nicht identisch) mit
dem obigen Problem in dem Sinne, dass jeder Optimalpunkt des konkaven Problems
auch ein Optimalpunkt des konvexen Problems ist, welches durch „minimiere
unter konvexen Nebenbedingungen“ entsteht. Die Optimalwerte stimmen aber im
Allgemeinen nicht überein.
Abstraktes konvexes Optimierungsproblem
Manchmal werden Probleme der Form
als abstraktes konvexes Optimierungsproblem bezeichnet. Sie besitzen
dieselben Lösbarkeitseigenschaften wie das obige Problem, sind aber mathematisch
schwerer zu handhaben, da Kriterien wie
algorithmisch schwer greifbar sind. Meist werden dann Funktionen gesucht, welche
die abstrakte Nebenbedingung
mittels Ungleichungen beschreiben, um das abstrakte Problem somit auf das obige
Problem zurückführen. Umgekehrt kann aber auch jedes konvexe Problem als ein
abstraktes konvexes Problem der Form „minimiere
unter der Nebenbedingung
“
formuliert werden. Hierbei ist
die Restriktionsmenge.
Mischformen
Die allgemeinste Form eines konvexen Problems besteht aus einer Mischform, die sowohl Ungleichungsrestriktionen, Gleichungsrestriktionen als auch abstrakte Nebenbedingungen verwendet. Aus den oben beschriebenen Gründen ist diese Form jedoch unpraktisch zu handhaben.
Lösbarkeit aus theoretischer Sicht
Abstrakte konvexe Probleme zeichnen sich durch einige starke Eigenschaften aus, die das Auffinden von globalen Minima erleichtern:
- Jedes lokale Minimum des Problems ist immer auch ein globales Minimum des Problems.
- Die Menge der optimalen Punkte ist konvex. Sind nämlich
optimal für das Problem, so ist aufgrund der Konvexität
, da
. Andererseits ist
für alle Punkte
der Restriktionsmenge
, da
und
globale Minima sind. Somit ist
für alle
.
- Ist die Zielfunktion strikt konvex, so ist der Optimalpunkt eindeutig.
Da jede Formulierung eines konvexen Problems in ein abstraktes Problem umgewandelt werden kann, übertragen sich alle diese Eigenschaften auf jede Formulierung des Problems.
Geschichte
Die Disziplin der konvexen Optimierung entstand unter anderem aus der konvexen Analysis. Die erste Optimierungs-Technik, welche als Gradientenverfahren bekannt ist, geht auf Gauß zurück. Im Jahre 1947 wurde das Simplex-Verfahren durch George Dantzig eingeführt. Des Weiteren wurden im Jahr 1968 erstmals Innere-Punkte-Verfahren durch Fiacco und McCormick vorgestellt. In den Jahren 1976 und 1977 wurde die Ellipsoid-Methode von David Yudin und Arkadi Nemirovski und unabhängig davon von Naum Schor zur Lösung konvexer Optimierungsprobleme entwickelt. Narendra Karmarkar beschrieb im Jahr 1984 zum ersten Mal einen polynomialen potentiell praktisch einsetzbaren Algorithmus für lineare Probleme. Im Jahr 1994 entwickelten Arkadi Nemirovski und Yurii Nesterov Innere-Punkte-Verfahren für die konvexe Optimierung, welche große Klassen von konvexen Optimierungsproblemen in polynomialer Zeit lösen konnten.
Bei den Karush-Kuhn-Tucker-Bedingungen wurden die notwendigen Bedingungen für die Ungleichheits-Einschränkung zum ersten Mal 1939 in der Master-Arbeit (unveröffentlicht) von William Karush aufgeführt. Bekannter wurden diese jedoch erst 1951 nach einem Konferenz-Paper von Harold W. Kuhn und Albert W. Tucker.
Vor 1990 lag die Anwendung der konvexen Optimierung hauptsächlich im Operations Research und weniger im Bereich der Ingenieure. Seit 1990 boten sich jedoch immer mehr Anwendungsmöglichkeiten in der Ingenieurwissenschaft. Hier lässt sich unter anderem die Kontroll- und Signal-Steuerung, die Kommunikation und der Schaltungsentwurf nennen. Darüber hinaus ist das Konzept vor allem für die Strukturmechanik effizient. Außerdem entstanden neue Problemklassen wie semidefinite und Kegel-Optimierung 2. Ordnung und robuste Optimierung.
Beispiel
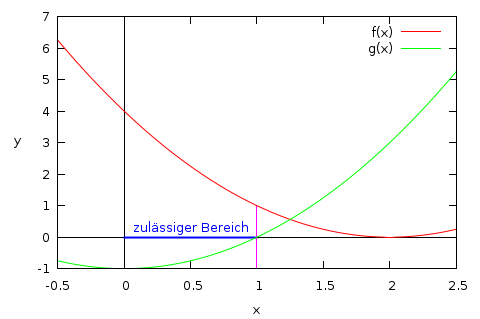
Als Beispiel wird ein eindimensionales Problem ohne Gleichungsnebenbedingungen und mit nur einer Ungleichungsnebenbedingung betrachtet:
Minimiere
mit
unter der Nebenbedingung:
Der zulässige Bereich ist gegeben durch die konvexe Menge
,
denn für Werte
ist
nicht erfüllt. Der Zeichnung kann entnommen werden, dass
für
den Optimalwert
annimmt.
Klassifikation und Verallgemeinerungen
Die konvexe Optimierung enthält weitere Klassen von Optimierungsproblemen, die sich alle durch eine spezielle Struktur auszeichnen:
- Konische
Programme: Es werden verallgemeinerte
Ungleichungen verwendet, ansonsten sind alle Funktionen affin. Konische
Programme haben wiederum drei Teilgebiete:
- Semidefinite Programme verwenden den Kegel der positiv semidefiniten Matrizen, haben also als Variable eine Matrix. Die verwendete verallgemeinerte Ungleichung ist dann die Loewner-Halbordnung.
- Die SOCPs (Second Order Cone Program) verwenden den second-order cone, der auch Lorentz-Kegel genannt wird.
- Auch lineare Optimierungsprobleme lassen sich als konische Programme formulieren.
Außerdem wird unterschieden, ob die verwendeten Funktionen stetig differenzierbar sind oder nicht.
Unter gewissen Voraussetzungen fallen noch folgende Problemklassen unter die konvexe Optimierung:
- Quadratische Programme und Quadratische Programme mit quadratischen Nebenbedingungen sind konvexe Probleme, wenn alle auftretenden Matrizen positiv semidefinit sind.
- Geometrische Programme sind per se keine konvexen Probleme, lassen sich aber durch elementare Substitutionen in eine konvexe Form überführen.
Verallgemeinerungen, die noch einige Eigenschaften einer konvexen Funktion erhalten, machen gewisse erweiterte Begriffe der konvexen Optimierung möglich.
- Pseudokonvexe Funktionen sind eine Klasse von differenzierbaren Funktionen, bei denen ein globales Minimum vorliegt, wenn die Ableitung verschwindet.
- Bei quasikonvexen Funktionen sind die Subniveaumengen alle konvex. Lässt man somit quasikonvexe Funktionen als Ungleichungsrestriktionen zu, so ist die Restriktionsmenge als Schnitt der Subniveaumengen immer noch eine konvexe Menge. Man erhält somit ein abstraktes konvexes Optimierungsproblem.
- K-konvexe
Funktion verwenden verallgemeinerte
Ungleichungen, um Konvexität für Halbordnungen auf dem
zu verallgemeinern. Dabei werden
echte Kegel im
definiert und dementsprechend
Funktionen
, die K-konvex bezüglich des Kegels
und der verallgemeinerten Ungleichung
sind. Das Problem lautet dann
- für eine konvexe Funktion
und eine passend dimensionierte Matrix
und einen Vektor
. Da auch die Subniveaumengen einer K-konvexen Funktion konvex sind, liefert dies auch wieder ein abstraktes konvexes Optimierungsproblem.
- Eine weitere Verallgemeinerung sind die fast konvexen Funktionen. Sie bilden im Allgemeinen kein abstraktes konvexes Optimierungsproblem mehr, dafür gilt bei ihnen wie bei konvexen Problemen die starke Dualität, wenn sie die Slater-Bedingung erfüllen.
- Allgemeiner lassen sich konvexe Abbildungen für jeden reellen Vektorraum mit Ordnungskegel definieren.
Optimalitätsbedingungen
Für konvexe Probleme gibt es einige wichtige Optimalitätskriterien. Zuerst werden die notwendigen Kriterien beschrieben, das heißt, wenn ein Optimum erreicht wird, dann sind diese Kriterien erfüllt. Danach die hinreichenden Kriterien, das heißt, wenn diese Kriterien in einem Punkt erfüllt sind, dann handelt es sich um einen Optimalpunkt.
Notwendige Kriterien
Karush-Kuhn-Tucker-Bedingungen
Die Karush-Kuhn-Tucker-Bedingungen (auch bekannt als die
KKT-Bedingungen) sind eine Verallgemeinerung der Lagrange-Multiplikatoren
von Optimierungsproblemen unter Nebenbedingungen und finden in der
fortgeschrittenen neoklassischen
Theorie Anwendung. Ein zulässiger Punkt
des konvexen Problem erfüllt die KKT-Bedingungen, wenn gilt
Diese Bedingungen werden die Karush-Kuhn-Tucker-Bedingungen oder kurz KKT-Bedingungen genannt.
Ein Punkt
heißt dann Karush-Kuhn-Tucker-Punkt oder kurz KKT-Punkt des obigen
Optimierungsproblems, wenn er die obigen Bedingungen erfüllt.
Das eigentliche notwendige Optimalitätskriterium lautet nun: Ist ein Punkt
ein lokales (und aufgrund der Konvexität auch globales) Minimum des konvexen
Problems, und erfüllt er gewisse Regularitätsvoraussetzungen, so gibt es
,
so dass
ein KKT-Punkt ist. Gängige Regularitätsbedingungen (auch constraint
qualifications genannt) sind die LICQ,
die MFCQ,
die Abadie
CQ oder speziell für konvexe Probleme die Slater-Bedingung.
Mehr Regularitätsvoraussetzungen finden sich im Hauptartikel zu den
KKT-Bedingungen.
Fritz-John-Bedingungen
Die Fritz-John-Bedingungen oder FJ-Bedingungen sind eine Verallgemeinerung
der KKT-Bedingungen und kommen im Gegensatz zu diesen ohne
Regularitätsvoraussetzungen aus. Unter gewissen Umständen sind beide Bedingungen
äquivalent. Ein Punkt
heißt Fritz-John-Punkt oder kurz FJ-Punkt des konvexen Problems,
wenn er die folgenden Bedingungen erfüllt:
Diese Bedingungen werden die Fritz-John-Bedingungen oder kurz FJ-Bedingungen genannt.
Ist der Punkt
lokales (und aufgrund der Konvexität auch globales) Minimum des
Optimierungsproblems, so gibt es
,
so dass
ein FJ-Punkt ist und
ungleich dem Nullvektor ist.
Hinreichende Kriterien
Ist
ein KKT-Punkt, so ist
ein globales Minimum des konvexen Problems. Somit sind die KKT-Bedingungen im
konvexen Fall schon hinreichend für die Optimalität des Punktes. Insbesondere
werden dazu keine weiteren Regularitätsvoraussetzungen benötigt. Da sich zeigen
lässt, dass man aus jedem FJ-Punkt einen KKT-Punkt konstruieren kann, wenn
ist, sind auch schon die FJ-Bedingungen hinreichend für die Optimalität, wenn
gilt.
Kriterien für nicht differenzierbare Funktionen
Sind einige der verwendeten Funktionen des konvexen Optimierungsproblems
nicht differenzierbar, so kann man noch auf die Sattelpunktcharakterisierung von
Optimalpunkten zurückgreifen. Mittels der Lagrange-Funktion lässt sich dann
zeigen, dass jeder Sattelpunkt der Lagrange-Funktion ein Optimallösung ist.
Umgekehrt ist
eine Optimallösung und die Slater-Bedingung
erfüllt, so kann man die Optimallösung zu einem Sattelpunkt der
Lagrange-Funktion erweitern.
Konkretes Vorgehen
Lagrange-Funktion
Zunächst wird die folgende abkürzende Schreibweise eingeführt:
,
wobei
der Vektor aus allen Multiplikatoren ist.
Lagrangesche Multiplikatorenregel für das konvexe Problem
Vergleiche hierzu auch mit Lagrangesche Multiplikatorenregel. Konkretes Vorgehen:
- Überprüfe, ob alle auftretenden Funktionen stetig partiell differenzierbar sind. Falls nein, ist diese Regel nicht anwendbar.
- Gibt es einen zulässigen Punkt
, für den gilt:
? Falls ja, dann ist
optimal. Sonst fahre mit dem nächsten Schritt fort.
- Bestimme den Gradienten
der Lagrange-Funktion.
- Löse das System
, wobei kein Multiplikator negativ sein darf. Falls eine Restriktion nicht aktiv ist, muss der zugehörige Multiplikator sogar gleich
sein. Findet man eine Lösung
, so ist diese optimal.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 17.12. 2021