Johann Carl Friedrich Gauß

deutscher Mathematiker, Astronom, Geodät und Physiker

geboren: 30. April 1777 in Braunschweig
gestorben: 23. Februar 1855 in Göttingen

Professor an der Georg-August-Universität Göttingen 1807;
Mitglied der Akademie Sankt Petersburg 1802;
Auswärtiges Mitglied der Bayerischen Akademie der Wissenschaften 1820;
Auswärtiges Mitglied der American Academy of Arts and Sciences 1822;
Copley-Medaille der Royal Society 1838;
Aufnahme in die Friedensklasse des Ordens Pour le Mérite 1842;
Geheimer Hofrat in Wien 1845;

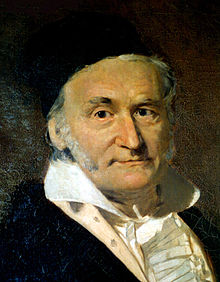
Bereits 1856 ließ der König von Hannover Gedenkmedaillen mit dem Bild von Gauß und der Inschrift „Mathematicorum Principi“ (deutsch: „dem Fürsten der Mathematiker“) prägen. Da Gauß nur einen Bruchteil seiner Entdeckungen veröffentlichte, erschloss sich der Nachwelt die Tiefgründigkeit und Reichweite seines Werks in vollem Umfang erst, als 1898 sein Tagebuch entdeckt und ausgewertet wurde und als der Nachlass bekannt wurde.

Einige Anekdoten besagen, dass bereits der dreijährige Carl Friedrich seinen Vater bei der Lohnabrechnung korrigierte. Später sagte Gauß von sich selbst, er habe das Rechnen vor dem Sprechen gelernt.
Mit 14 Jahren galt Gauß als mathematischer „Wunderknabe“.
Mit finanzieller Unterstützung des Herzogs von Braunschweig konnte Gauß von 1792 bis 1795 am Collegium Carolinum studieren.

Im Oktober 1795 wechselte Gauß an die Universität Göttingen. Dort hörte er Vorlesungen über klassische Philologie, Mathematik, Experimentalphysik und sehr wahrscheinlich Astronomie.
Mit 18 Jahren entdeckte er einige Eigenschaften der Primzahlverteilung und fand die Methode der kleinsten Quadrate, bei der es darum geht, die Summe der Quadrate von Abweichungen zu minimieren, ohne zunächst etwas darüber zu publizieren. Nachdem Adrien-Marie Legendre 1805 seine „Méthode des moindres carrés“ in einer Abhandlung veröffentlicht hatte und Gauß seine Ergebnisse erst 1809 bekannt machte, entstand daraus ein Prioritätsstreit.

Gauß erfasste früh den Nutzen komplexer Zahlen, so in seiner Doktorarbeit von 1799, die einen Beweis des Fundamentalsatzes der Algebra enthält. Dieser Satz besagt, dass jede algebraische Gleichung mit Grad größer als null mindestens eine reelle oder komplexe Lösung besitzt. Den älteren Beweis von Jean-Baptiste le Rond d’Alembert kritisierte Gauß als ungenügend, aber auch sein eigener Beweis erfüllt noch nicht die späteren Ansprüche an topologische Strenge. Gauß kam auf den Beweis des Fundamentalsatzes noch mehrfach zurück und gab neue Beweise 1815 und 1816.
Gauß kannte spätestens 1811 die geometrische Darstellung komplexer Zahlen in einer Zahlenebene (gaußsche Zahlenebene), die schon Jean-Robert Argand 1806 und Caspar Wessel 1797 gefunden hatten. 1849 veröffentlicht er zu seinem Goldenen Doktorjubiläum eine verbesserte Version seiner Dissertation, in der er im Gegensatz zur ersten Version explizit komplexe Zahlen benutzt.
Nach seiner Promotion lebte Gauß in Braunschweig von dem kleinen Gehalt, das ihm der Herzog zahlte, und arbeitete an seinem Werk Disquisitiones Arithmeticae.

Einen Ruf an die Petersburger Akademie der Wissenschaften lehnte Gauß aus Dankbarkeit gegenüber seinem Gönner, dem Herzog von Braunschweig, und wohl in der Hoffnung, dass dieser ihm eine Sternwarte in Braunschweig bauen würde, ab.
Gauß wurde im November 1807 Professor an der Georg-August-Universität Göttingen und Direktor der dortigen Sternwarte.

Er wurde in Göttingen auf dem Albani-Friedhof begraben.