
Quader

Quader mit
Raumdiagonale d
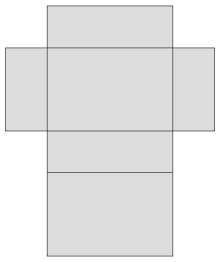
Auseinander
geklapptes Netz
eines Quaders
Ein Quader (auch Rechtkant und zuweilen Rechtflach) ist ein Körper, der von sechs Rechtecken begrenzt wird.
Ein Quader besitzt
- sechs Seitenflächen, die im rechten Winkel aufeinander stehen,
- acht rechtwinkelige Ecken und
- zwölf Kanten, von denen jeweils vier gleiche Längen besitzen und zueinander parallel sind.
Gegenüberliegende Flächen eines Quaders sind kongruent (deckungsgleich).
| Formeln zum Quader | ||
|---|---|---|
| Kantenlängen | ||
| Volumen | ||
| Oberflächeninhalt | ||
| Länge der Raumdiagonalen | ||
Spezielle Quader
Im Sonderfall gleicher Kantenlängen ,
bei dem alle Flächen des Quaders Quadrate sind,
ergibt sich ein Würfel.
Im Fall, dass genau zwei Kantenlängen gleich sind, ergibt sich ein
quadratisches gerades Prisma (
),
man spricht gelegentlich von einer quadratischen Platte (
)
bzw. einer quadratischen Säule (
).
Symmetrie
Quader sind punktsymmetrisch. Der Symmetriepunkt ist der Schnittpunkt der Raumdiagonalen. Im Gegensatz zum Würfel stellen die Raumdiagonalen keine (dreizähligen) Drehachsen dar.
Verallgemeinerungen
- Ein dreidimensionaler Körper mit sechs paarweise parallelen Flächen heißt Parallelepiped, unabhängig von der Rechtwinkligkeit. Somit ist jeder Quader ein rechtwinkliges Parallelepiped.
- Jeder Quader ist ein Prisma mit rechteckiger Grundfläche.
- Gelegentlich wird der Begriff des Quaders auf
-dimensionale Räume erweitert, sodass speziell für
ein Rechteck als zweidimensionaler, ein Intervall bzw. eine Strecke als eindimensionaler und ein Punkt als nulldimensionaler Quader bezeichnet werden kann. Bei höherdimensionalen Polytopen sind die Begriffe Hyperquader, Hyperrechteck,
-dimensionaler Quader oder auch
-dimensionales Intervall gebräuchlich.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 12.10. 2021