Schnittpunkt
Ein Schnittpunkt ist in der Mathematik ein gemeinsamer Punkt zweier Kurven in der Ebene oder im Raum. Der allgemeine Sprachgebrauch versteht unter Schnittpunkt jenen zweier Geraden, was jedoch im mathematischen Kurvenbegriff enthalten ist. Im Raum gibt es noch den Schnittpunkt einer Kurve mit einer Fläche. Im einfachsten Fall schneidet eine Gerade eine Ebene.
Die Bestimmung eines Schnittpunktes ist in den beiden Fällen Gerade-Gerade und Gerade-Ebene einfach (s. unten). Im Allgemeinen führt die Bestimmung von Schnittpunkten auf nicht lineare Gleichungen, die man in der Praxis mit einem Newton-Verfahren löst. Schnittpunkte einer Gerade mit einem Kegelschnitt (Kreis, Hyperbel, Ellipse, Parabel) oder einer Quadrik (Kugel, Ellipsoid, Hyperboloid, …) führen auf quadratische Gleichungen und sind auch noch relativ leicht lösbar. Für den Schnitt einer Gerade mit Ebene/Kugel/Zylinder/Kegel bietet die darstellende Geometrie Methoden, um Schnittpunkte zeichnerisch zu bestimmen.
Schnittpunkt in der Ebene
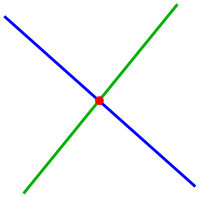
Schnittpunkt zweier Geraden
Für den Schnittpunkt zweier nicht paralleler
- Geraden (gegeben in Koordinatenform)
ergibt sich mit der Cramerschen
Regel für die Koordinaten des Schnittpunktes
Falls
ist, sind die beiden Geraden parallel.
- Für eine Gerade durch die Punkte
und
- und eine Gerade durch die Punkte
und
- Berechnet man den Schnittpunkt, indem man zuvor die Zweipunkteformen in Koordinatenformen umrechnet.
- Der Schnittpunkt
ergibt sich zu
- und
Schnittpunkt zweier Strecken
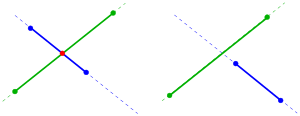
Sind zwei nicht parallele Strecken
und
gegeben, so müssen sie sich nicht schneiden. Denn der Schnittpunkt
der zugehörigen Geraden muss nicht in beiden Strecken enthalten sein. Um
letzteres zu klären, stellt man beide Strecken parametrisiert dar:
,
Schneiden sich die Strecken, so muss der gemeinsame Punkt
der zugehörigen Geraden Parameter
haben mit der Eigenschaft
.
Die Schnittparameter
sind Lösung des linearen Gleichungssystems
Dieses löst man (wie oben) mit der Cramerschen Regel, überprüft die
Schnittbedingung
und setzt
oder
in die zugehörige Parameterdarstellung ein, um schließlich den Schnittpunkt
zu erhalten.
Beispiel: Für die Strecken
und
erhält man das Gleichungssystem
und .
D. h. die Strecken schneiden sich und der Schnittpunkt ist
.
Bemerkung: Betrachtet man Geraden durch zwei Punktepaare (nicht
Strecken !), so kann man die Bedingung
ignorieren und erhält mit dieser Methode den Schnittpunkt der beiden Geraden (s.
vorigen Abschnitt).
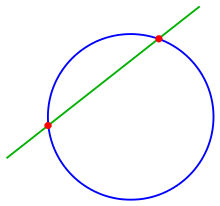
Schnittpunkte einer Geraden mit einem Kreis
Um den Schnitt der
- Gerade
mit dem Kreis
zu berechnen, wird zunächst das System durch Setzen von
und
so verschoben, dass der Kreismittelpunkt im Nullpunkt liegt. Dadurch ergibt sich
als neue Kreisgleichung
und als neue Geradengleichung
mit
.
Durch Auflösen der Geradengleichung nach
oder
,
Einsetzen in die Kreisgleichung, Anwenden der Lösungsformel für quadratische
Gleichungen und anschließendes Rückgängigmachen der Verschiebung ergeben sich
dann die Schnittpunkte
mit
sofern
gilt. Im Fall der Gleichheit gibt es nur einen Schnittpunkt und die Gerade ist
eine Tangente des Kreises.
Bemerkung: Die Schnittpunkte einer Gerade mit einer Parabel oder einer Hyperbel lassen sich analog durch Lösen einer quadratischen Gleichung bestimmen.
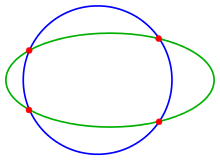
Schnittpunkte zweier Kreise
Die Bestimmung der Schnittpunkte zweier Kreise
lässt sich durch Subtraktion der beiden Gleichungen auf das Problem Schnittpunkte der Gerade
mit einem der beiden Kreise zurückführen (s. o.).
Sonderfall :
In diesem Fall hat der erste Kreis den Nullpunkt als Mittelpunkt und der zweite
Mittelpunkt liegt auf der x-Achse. Dadurch vereinfacht sich die Gleichung der
Potenzgerade zu
und für die Schnittpunkte
ergibt sich
Falls
ist, schneiden sich die Kreise nicht. Im Fall
berühren sich die Kreise.
Der allgemeine Fall lässt sich immer durch eine geeignete Verschiebung und Drehung auf diesen Sonderfall zurückführen.
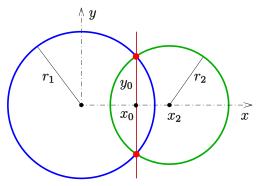
Alternative Berechnungsmethode
Analog zu den obigen Kreisgleichungen, sind die Mittelpunkte der Kreise wie folgt beschreibbar:
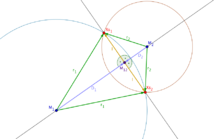
Die Bezeichnungen sind der nebenstehenden Grafik zu entnehmen. Des Weiteren
lassen sich der Vektor
und
wie folgt beschreiben:
(Hinweis:
stellt die Vektornorm
dar, bzw. die Länge des Vektors)
Wobei
die Radien der Kreise repräsentieren. Dieser Vektor
verbindet also die Punkte
und
.
Auf diese Formel kommt man durch geometrische Überlegungen. Und zwar muss anhand
der in der Grafik zu sehenden Dreiecke
die folgende Gleichung nach dem Satz
des Pythagoras erfüllt sein.
Weiterhin gilt, dass die Summe der Längen von
und
dem Mittelpunktsabstand der Kreise entspricht:
Folglich lässt sich der Mittelpunktsabstand prozentual mit dem Parameter
auf die Längen von
und
aufteilen:
Mit den Gleichungen (1) und (2) lässt sich damit der Parameter
bestimmen:
Nun benötigt man einen zum Richtungsvektor zwischen
und
orthogonalen
Einheitsvektor. Dies lässt sich dann wie folgt darstellen:
Die Schnittpunkte
lassen sich nun wie folgt beschreiben:
Schnittpunkte zweier Kegelschnitte
Die Aufgabe, die Schnittpunkte einer Ellipse/Hyperbel/Parabel mit einer Ellipse/Hyperbel/Parabel zu bestimmen, führt bei Elimination einer Koordinate i.a. auf eine Gleichung vierten Grades, die nur in speziellen Fällen leicht lösbar ist. Die Schnittpunkte lassen sich allerdings auch iterativ mit Hilfe des 1- bzw. 2-dimensionalen Newton-Verfahrens bestimmen, je nachdem man a) beide Kegelschnitte implizit (→ 2-dim. Newton) oder b) einen implizit und den anderen parametrisiert darstellt (→ 1-dim. Newton). Siehe hierzu den nächsten Abschnitt.
Schnittpunkt zweier Kurven
Zwei in der Ebene
liegende, stetig differenzierbare Kurven (also Kurven ohne „Knick“) haben einen
Schnittpunkt, wenn sie einen Punkt der Ebene gemeinsam haben und die
beiden Kurven in diesem Punkt entweder
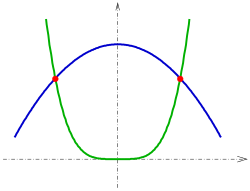
- a) unterschiedliche Tangenten aufweisen (transversales Schneiden), oder
- b) gemeinsame Tangenten haben und sich in dem Punkt kreuzen (berührendes Schneiden, siehe Bild).
Falls die beiden Kurven zwar einen gemeinsamen Punkt
und dort eine gemeinsame Tangente haben, aber sich nicht kreuzen,
berühren sie sich in
.
Da berührendes Schneiden eher selten vorkommt und rechnerisch sehr aufwendig zu behandeln ist, wird im Folgenden stets transversales Schneiden vorausgesetzt. Um es nicht immer wieder erwähnen zu müssen, werden auch die jeweils nötigen Differenzierbarkeits-Bedingungen vorausgesetzt. Die Bestimmung von Schnittpunkten führt immer wieder auf das Problem, eine Gleichung mit einer bzw. zwei Gleichungen mit zwei Unbekannten lösen zu müssen. Die Gleichungen sind im Allgemeinen nicht linear und können dann beispielsweise mit dem 1- oder 2-dimensionalen Newton-Verfahren numerisch gelöst werden. Im Folgenden werden die einzelnen Fälle und die zu lösenden Gleichungen beschrieben:
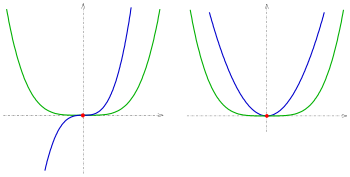
- Falls beide Kurven explizit vorliegen:
liefert Gleichsetzen die Gleichung
- Falls beide Kurven parametrisiert vorliegen:
.
- Gleichsetzen liefert zwei Gleichungen für zwei Unbekannte:
- Falls eine Kurve parametrisiert und die andere implizit gegeben
sind:
.
- Dies ist nach dem expliziten der einfachste Fall. Denn man muss hier nur
die Parameterdarstellung von
in die Gleichung
von
einsetzen und erhält die Gleichung
- Falls beide Kurven implizit gegeben sind:
.
- Ein Schnittpunkt ist hier die Lösung des im Allgemeinen nichtlinearen
Gleichungssystems
Die für das jeweilige Newton-Verfahren nötigen Startwerte lassen sich aus
einer Visualisierung der beiden Kurven gewinnen. Eine parametrisiert oder
explizit gegebene Kurve lässt sich leicht visualisieren, da man zu vorgegebenem
Parameter
bzw.
direkt einen Punkt berechnen kann. Für implizit gegebene Kurven ist dies nicht
so einfach. Hier muss man im Allgemeinen mit Hilfe von Startpunkten und einem
Iterationsverfahren Kurvenpunkte berechnen.
Beispiele:
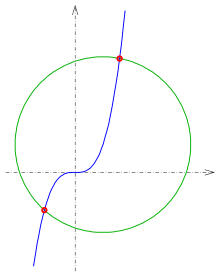
- 1:
und Kreis
(s. Bild).
- Es ist die Newton-Iteration
für
durchzuführen. Als Startwerte kann man −1 und 1,5 wählen.
- Die Schnittpunkte sind: (−1,1073; −1.3578) und (1,6011; 4,1046)
- Es ist die Newton-Iteration
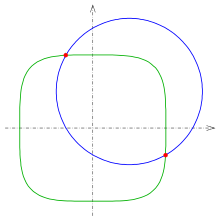
- 2:
(s. Bild).
- Es ist die Newton-Iteration
durchzuführen, wobei
die Lösung des linearen Gleichungssystems
an der Stelle
ist. Als Startpunkte kann man (−0,5; 1) und (1; −0,5) wählen.
- Das lineare Gleichungssystem löst man am einfachsten mit der Cramerschen Regel.
- Als Schnittpunkte ergeben sich (−0.3686; 0,9953) und (0,9953; −0,3686).
Schnittpunkt zweier Polygone
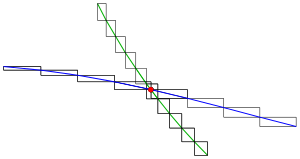
Falls man Schnittpunkte zweier Polygone sucht, kann man jede Teilstrecke des einen Polygons mit jeder Teilstrecke des anderen Polygons auf Schneiden untersuchen (s. oben: Schnitt zweier Strecken). Für Polygone mit vielen Teilstrecken ist diese einfache Methode sehr zeitaufwändig. Durch sogenannte Fenstertests lässt sich die Rechenzeit deutlich reduzieren. Dabei fasst man mehrere Teilstrecken zu einem Teilpolygon zusammen und berechnet das zugehörige Fenster, das ist das minimale achsenparallele Rechteck, das das Teilpolygon enthält. Bevor aufwändig ein Schnittpunkt zweier Teilpolygone berechnet wird, werden die zugehörigen Fenster auf Überlappung getestet.
Schnittpunkte im Raum
Im 3-dimensionalen Raum spricht man von einem Schnittpunkt (gemeinsamer Punkt) einer Kurve mit einer Fläche. Bei den folgenden Überlegungen sollen (wie oben) nur die transversalen Schnitte einer Kurve mit einer Fläche behandelt werden.
Schnittpunkt einer Geraden mit einer Ebene
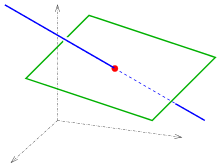
Eine Gerade wird im Raum in der Regel durch eine Parameterdarstellung
und eine Ebene
durch eine Gleichung
beschrieben. Durch Einsetzen der Parameterdarstellung der Gerade in die Ebenengleichung ergibt
sich die lineare Gleichung
für den Parameter
des Schnittpunktes
.
(Falls die lineare Gleichung keine Lösung besitzt, ist die Gerade parallel zur
Ebene. Falls die Gleichung für alle
erfüllt ist, ist die Gerade in der Ebene enthalten.)
Schnittpunkt dreier Ebenen
Ist eine Gerade als Schnitt zweier nicht paralleler Ebenen
gegeben und soll mit einer dritten Ebene
geschnitten werden, muss der gemeinsame Punkt der 3 Ebenen bestimmt werden.
Drei Ebenen
mit linear unabhängigen Normalenvektoren
besitzen den Schnittpunkt
Zum Beweis überzeuge man sich von
unter Beachtung der Regeln für ein Spatprodukt.
Schnittpunkte einer Kurve mit einer Fläche
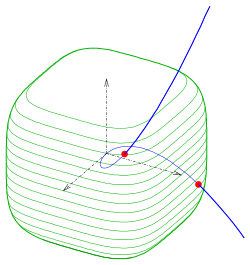
Analog wie im ebenen Fall führen die folgenden Fälle zu im Allgemeinen nicht linearen Gleichungssystemen, die mit einem 1- bzw. 3-dimensionalen Newton-Verfahren gelöst werden können:
- parametrisierte Kurve
und
- parametrisierte Fläche
- parametrisierte Kurve
und
- implizite Fläche
Beispiel:
- parametrisierte Kurve
und
- implizite Fläche
(siehe Bild)
- Zu lösende Gleichung:
- Die Schnittpunkte sind: (−0,8587; 0,7374; −0,6332), (0,8587; 0,7374; 0,6332).
Bemerkung: Eine Gerade kann auch in einer Ebene enthalten sein. Dann
gibt es unendlich viele gemeinsame Punkte. Auch eine Kurve kann teilweise oder
vollständig in einer Fläche enthalten sein (siehe Kurven auf der Fläche ).
In diesen Fällen spricht man aber nicht mehr von Schnittpunkt.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 02.05. 2021