Kegelschnitt

Kegelschnitte:
(1) liefert die Parabel, (2) Kreis und Ellipse, (3) die Hyperbel

Ein Kegelschnitt (lateinisch sectio conica, englisch conic section) ist eine Kurve, die entsteht, wenn man die Oberfläche eines Doppelkegels mit einer Ebene schneidet. Enthält die Schnittebene die Kegelspitze, so entsteht als Schnitt entweder ein Punkt oder eine Gerade oder ein sich schneidendes Geradenpaar. Ist die Spitze nicht enthalten, so entstehen die nicht ausgearteten Kegelschnitte Ellipse, Kreis (eine Sonderform der Ellipse), Parabel oder Hyperbel.

Der Nachweis, dass im nicht ausgearteten Fall wirklich diese in der Ebene als Ortskurven definierten Kurven entstehen, lässt sich ohne Rechnung mit Hilfe der Dandelinschen Kugeln führen. Der rechnerische Nachweis wird hier im Abschnitt Ebene Schnitte des Einheitskegels gegeben.

Ein Kegelschnitt kann auch als zweidimensionaler Sonderfall einer Quadrik angesehen werden und durch eine Gleichung 2. Grades, die allgemeine Kegelschnittgleichung, beschrieben werden.

Bettet man Ellipse, Hyperbel und Parabel in eine projektive Ebene ein, so entstehen projektive Kegelschnitte, die alle zueinander äquivalent sind, d.h., man kann sie durch geradentreue Abbildungen ineinander überführen.

Ellipse: Definition

Parabel: Definition

Hyperbel: Definition

Ausgeartete Kegelschnitte:
sich schneidendes Geradenpaar, paralleles Geradenpaar, eine Gerade, ein Punkt

Gleichungen der Kegelschnitte

Die Kegelschnitte können in einem geeigneten x-y-Koordinatensystem durch Gleichungen 2. Grades beschrieben werden:

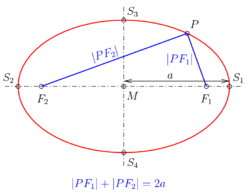
Ellipse mit Mittelpunkt M im Punkt (0,0) und der Hauptachse auf der x-Achse:

$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1, \quad b=|MS_3|, \qquad a,b\ne0\quad,$ (s. Bild). (Für ergibt sich ein Kreis.)
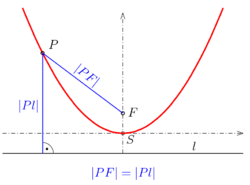
Parabel mit Scheitel im Punkt (0,0) und der Achse auf der y-Achse:

$y=ax^{2},\quad a={\frac {1}{4|SF|}},\qquad a\neq 0\quad ,$ (s. Bild).
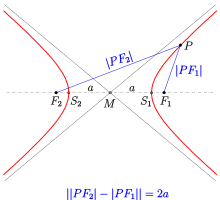
Hyperbel mit Mittelpunkt M im Punkt (0,0) und der Hauptachse auf der x-Achse:

${\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}=1,\quad b^{2}=|MF_{1}|^{2}-a^{2},\qquad a,b\neq 0\quad ,$ (s. Bild).
Sich schneidendes Geradenpaar mit Schnittpunkt im Punkt (0,0):

$a^{2}x^{2}-y^{2}=0,\ a\neq 0.$
Gerade durch den Punkt (0,0):

$x^{2}=0.$
Punkt, der Punkt (0,0):

$a^{2}x^{2}+b^{2}y^{2}=0,\ a,b\neq 0.$

Der Vollständigkeit halber werden noch zwei weitere Fälle hinzugenommen, die nicht als eigentliche Kegelschnitte auftreten, aber auch durch Gleichungen 2. Grades beschrieben werden:

Paralleles Geradenpaar:

$x^{2}=a^{2},\ a\neq 0.$
Die leere Menge:

$x^{2}+y^{2}=-1$ oder $x^{2}=-1$ .

Die letzten beiden Fälle können als ebene Schnitte eines geraden Kreiszylinders auftreten. Ein Kreiszylinder lässt sich als Grenzfall eines Kegels mit Kegelspitze im Unendlichen auffassen. Deshalb nimmt man diese beiden Fälle mit zu den Kegelschnitten.

Ebene Schnitte des Einheitskegels

Kegelschnitt-Fälle

Um festzustellen, dass die oben als Kegelschnitte bezeichneten Kurven/Punkte tatsächlich beim Schnitt eines Kegels mit einer Ebene auftreten, schneiden wir hier den Einheitskegel (gerader Kreiskegel) $K_{1}\colon x^{2}+y^{2}=z^{2}$ mit einer Ebene, die parallel zur y-Achse ist. Dies ist keine Einschränkung, da der Kegel rotationssymmetrisch ist. Ein beliebiger gerader Kreiskegel ist das affine Bild des Einheitskegels $K_{1}$ und Ellipsen/Hyperbeln/Parabeln/… gehen bei einer affinen Abbildung wieder in ebensolche über.

Gegeben: Ebene $\varepsilon \colon ax+cz=d\ ,$ Kegel $K_{1}\colon x^{2}+y^{2}=z^{2}$ .

Gesucht: Schnitt $\varepsilon \cap K_1$ .

Fall I: In diesem Fall ist die Ebene senkrecht und und . Eliminiert man aus der Kegelgleichung, so erhält man .
- Fall Ia: . In diesem Fall besteht der Schnitt aus dem Geradenpaar $t(0,1, \pm 1), \ t \in \R.$ .
- Fall Ib: $d \neq 0$ . Die obige Gleichung beschreibt jetzt eine Hyperbel in der y-z-Ebene. Also ist auch die Schnittkurve $\varepsilon \cap K_1$ selbst eine Hyperbel.
Fall II: . Eliminiert man aus der Kegelgleichung mit Hilfe der Ebenengleichung, so erhält man das Gleichungssystem
- Fall IIa: Für geht die Ebene durch die Kegelspitze und Gleichung (1) hat jetzt die Gestalt .
  
  Für ist der Schnitt der Punkt $P_{0}=(0,0,0)$ .
  
  Für ist der Schnitt die Gerade $t(c,0,-a), \ t \in \R.$
  
  Für ist der Schnitt das Geradenpaar $t(c/ \pm \sqrt{a^2-c^2}, 1, -a/ \pm \sqrt{a^2-c^2}) , \ t \in\R .$
- Fall IIb: Für $d \neq 0$ geht die Ebene nicht durch die Kegelspitze und ist nicht senkrecht.
  
  Für geht (1) in $x=-{\frac {c^{2}}{2ad}}y^{2}+{\frac {d}{2a}}$ über und die Schnittkurve ist eine Parabel.
  
  Für $c^{2}\neq a^{2}$ formen wir (1) um in ${\frac {(c^{2}-a^{2})^{2}}{d^{2}c^{2}}}\left(x+{\frac {ad}{c^{2}-a^{2}}}\right)^{2}+{\frac {c^{2}-a^{2}}{d^{2}}}y^{2}=1$ .
  
  Für ergibt sich als Schnittkurve eine Ellipse und
  
  für ergibt sich eine Hyperbel.

Zusammenfassung:

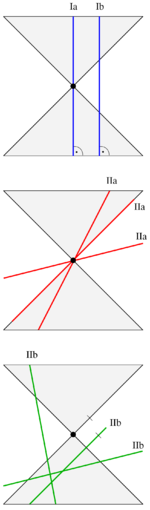
Enthält die Schnittebene die Kegelspitze nicht, entstehen die nicht ausgearteten Kegelschnitte (s. Bild zu Ib, IIb), nämlich eine Parabel, eine Ellipse oder eine Hyperbel, je nachdem, ob die Kegelachse von der Schnittebene unter dem gleichen, einem größeren oder einem kleineren Winkel geschnitten wird als von den Mantellinien des Kegels.
Liegt hingegen die Kegelspitze in der Schnittebene, entstehen die ausgearteten Kegelschnitte (s. Bild zu Ia, IIa), und zwar ein Punkt (nämlich die Kegelspitze), eine Gerade (nämlich eine Mantellinie) oder ein sich schneidendes Geradenpaar, (nämlich zwei Mantellinien).

Allgemeine Kegelschnittgleichung

Die allgemeine Gleichung für Kegelschnitte lautet

$ax^{2}+bxy+cy^{2}+dx+ey+f=0$

(man beachte, dass die Parameter a und b nicht diejenigen des vorhergehenden Abschnitts sind)

Die Parameter a,b,c sind im Speziellen nicht alle 0. Falls $a=b=c=0$ ist, beschreibt die Gleichung eine Gerade oder ganz $\mathbb {R} ^{2}$ .

Ellipse: Hauptachsentransformation

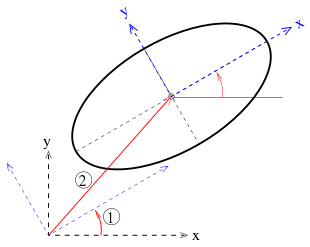
Es soll jetzt nachgewiesen werden, dass als Lösungsmengen der allgemeinen Kegelschnittgleichung nur die obigen 8 Fälle auftreten. Das Ziel erreichen wir in zwei wesentlichen Schritten, der Hauptachsentransformation:

Drehung des Koordinatensystems zur Beseitigung des Terms .
Verschiebung des Nullpunktes (Translation) so, dass möglichst die linearen Terme $\dots x+\dots y$ verschwinden.

1. Schritt: Falls $b\ne0$ , führen wir die Drehung

$(x,y)=(x'\cos\alpha-y'\sin\alpha,x'\sin\alpha+y'\cos\alpha)$

um den Winkel $\alpha$ mit $\tan(2\alpha)=\tfrac{b}{a-c}$ bzw. $\alpha=45^\circ$ , falls a=c

, durch.

Die Kegelschnittgleichung hat danach die Form

(statt

wurde wieder x,y

benutzt).

2.Schritt:

Falls $A\ne0$ ist, führt eine quadratische Ergänzung zum Term $A\left(x+{\tfrac {C}{2A}}\right)^{2}$ und damit zur Verschiebung $x'=x+\tfrac{C}{2A}$ .

Falls $B\ne0$ ist, führt eine quadratische Ergänzung zum Term $B\left(y+{\tfrac {D}{2B}}\right)^{2}$ und damit zur Verschiebung $y'=y+\tfrac{D}{2B}$ .

Nach diesen beiden Schritten hat die Kegelschnittgleichung (x’ und y’ werden wieder durch x,y ersetzt) schließlich die Form

mit $u,v\ne 0$ oder

II:

oder

mit $u\ne 0$ .

Es können nur die obigen 8 Fälle auftreten:

Im Fall I ergeben sich eine Ellipse oder eine Hyperbel oder die leere Menge, falls $w\ne 0$ ist, oder ein Punkt oder ein sich schneidendes Geradenpaar, falls w=0

ist.

Im Fall II ergeben sich eine Parabel, falls $v\ne 0$ ist, oder ein paralleles Geradenpaar oder eine Gerade oder die leere Menge, falls v=0

ist.

Bei den hier durchgeführten Transformationen (Drehung, Verschiebung) wird die geometrische Form des durch die ursprüngliche Gleichung beschriebenen Kegelschnitts nicht verändert. Parameter wie Halbachsen bei Ellipsen und Hyperbel oder Brennweite bei der Parabel oder Winkel/Abstand zwischen sich schneidenden/parallelen Geraden lassen sich an dem transformierten Kegelschnitt ablesen.

Bemerkung: Der quadratische Anteil der allgemeinen Kegelschnittgleichung lässt sich auch mit Hilfe einer 2×2-Matrix schreiben:

${\begin{pmatrix}x&y\end{pmatrix}}{\begin{pmatrix}a&b/2\\b/2&c\end{pmatrix}}{\begin{pmatrix}x\\y\end{pmatrix}}+dx+ey+f=0.$

Da eine Drehung und eine Verschiebung das Vorzeichen der Determinante $\delta=ac-\tfrac{b^2}{4}$ der 2×2-Matrix nicht verändert, führt $\delta \neq 0$ auf den Fall I und $\delta =0$ auf den Fall II. Weiß man, dass die ursprüngliche Kegelschnittgleichung einen nicht ausgearteten Kegelschnitt darstellt, kann man an der Determinante $\delta$ schon erkennen, ob es sich um eine Ellipse ( $\delta >0$ ) oder eine Hyperbel ( $\delta <0$ ) oder eine Parabel ( $\delta =0$ ) handelt.

Bemerkung:

Da die allgemeine Kegelschnittgleichung nur bis auf einen Faktor durch die 6 Koeffizienten bestimmt ist, sind für die Bestimmung der Koeffizienten 5 Punkte (Gleichungen) nötig. Aber: Nicht jede Wahl von 5 Punkten bestimmen einen Kegelschnitt eindeutig. (Gegenbeispiel: 4 Punkte auf einer Gerade, 1 Punkt nicht auf der Gerade.) Ein nicht ausgearteter Kegelschnitt (Ellipse, Hyperbel, Parabel) ist durch 5 Punkte, wobei keine 3 auf einer Gerade liegen, eindeutig bestimmt. Eine elegante Formel für den nicht ausgearteten Fall benutzt eine 6×6-Determinante:

${\begin{vmatrix}x^{2}&xy&y^{2}&x&y&1\\x_{1}^{2}&x_{1}y_{1}&y_{1}^{2}&x_{1}&y_{1}&1\\x_{2}^{2}&x_{2}y_{2}&y_{2}^{2}&x_{2}&y_{2}&1\\x_{3}^{2}&x_{3}y_{3}&y_{3}^{2}&x_{3}&y_{3}&1\\x_{4}^{2}&x_{4}y_{4}&y_{4}^{2}&x_{4}&y_{4}&1\\x_{5}^{2}&x_{5}y_{5}&y_{5}^{2}&x_{5}&y_{5}&1\\\end{vmatrix}}=0\quad ,$ ( $(x_{i},y_{i}),i=1,\dots ,5$ sind die vorgegebenen Punkte.)
Ein Kreis ist schon durch 3 Punkte (nicht auf einer Geraden) eindeutig bestimmt. Die Gleichung erhält man durch die 4×4-Determinante

${\begin{vmatrix}x^{2}+y^{2}&x&y&1\\x_{1}^{2}+y_{1}^{2}&x_{1}&y_{1}&1\\x_{2}^{2}+y_{2}^{2}&x_{2}&y_{2}&1\\x_{3}^{2}+y_{3}^{2}&x_{3}&y_{3}&1\\\end{vmatrix}}=0$ .

Beispiel: Der Kegelschnitt durch die 5 Punkte $(1,0),(-1,0),(0,1),(-1,-1),(1,1)$ hat nach Ausrechnen obiger Determinante die Gleichung $-4x^{2}+4xy-4y^{2}+4=0$ oder nach Vereinfachung: $x^{2}-xy+y^{2}-1=0$ . Die Hauptachsentransformation erfolgt mit einer Drehung um $45^{\circ }$ . Eine Verschiebung ist nicht nötig. Der Kegelschnitt hat die transformierte Gleichung $\tfrac{x^2}{2}+\tfrac{3}{2}y^2-1=0$ und ist eine Ellipse.

Scheitelgleichung einer Kegelschnittschar

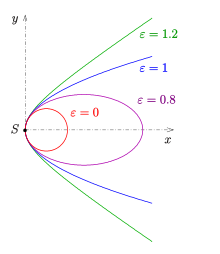
Kegelschnitt-Schar: p fest, $\varepsilon$ variabel

Die Schar der nicht ausgearteten Kegelschnitte, deren Achse die -Achse ist und die im Punkt (0,0) einen Scheitel haben, lässt sich durch die Gleichung

$y^2= 2px +(\varepsilon^2 -1) x^2 \qquad, \ p>0 \ , \varepsilon\ge 0$

beschreiben (zum Beweis siehe Leitlinien-Eigenschaft der Hyperbel). Für

$\varepsilon=0$ erhält man einen Kreis,

für $0<\varepsilon <1$ eine Ellipse,

für $\varepsilon =1$ eine Parabel und

für $\varepsilon>1$ eine Hyperbel.

$\varepsilon$ ist die numerische Exzentrizität.

ist die Weite des Kegelschnitts, gemessen am Brennpunkt senkrecht zur Achse.

ist der Scheitelkrümmungskreisradius im Scheitel (0,0)

Für Ellipsen und Hyperbeln ist $\varepsilon=e/a$ , wobei die große Halbachse und die lineare Exzentrizität ist. Im Fall einer Ellipse ist (a,0)

der Mittelpunkt und (a-e,0)

ein Brennpunkt. Im Fall einer Hyperbel ist (-a,0)

der Mittelpunkt und (e-a,0)

ein Brennpunkt. Im Fall einer Parabel ist $(\tfrac{p}{2},0)$ der Brennpunkt. Für den Kreis (mit $\varepsilon=0$ ) liegt der Mittelpunkt bei $(p,0)$ und der Radius ist .

Polargleichung einer Kegelschnittschar

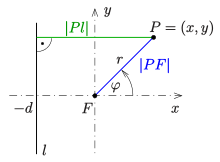
Kegelschnitt: zur Leitliniendefinition

Kegelschnittschar mit gemeinsamem Brennpunkt in Polarkoordinaten

Die Leitlinieneigenschaft der nicht ausgearteten Kegelschnitte lautet:

Die Menge der Punkte der euklidischen Ebene, deren Abstände zu einer vorgegebenen Geraden und einem vorgegebenen Punkt die Bedingung ${\frac {|PF|}{|Pl|}}=\varepsilon >0$ ist konstant, erfüllen, ist eine Ellipse, falls $0<\varepsilon <1$ , eine Parabel, falls $\varepsilon =1$ , eine Hyperbel, falls $\varepsilon>1$ ist.

Ist der Punkt der Nullpunkt und hat die Gerade die Gleichung $x=-d$ , so gilt in Polarkoordinaten (s. Bild):

${\frac {|PF|}{|Pl|}}={\frac {r}{r\cos \varphi +d}}=\varepsilon \ .$

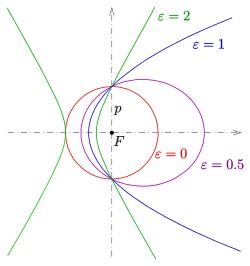
Auflösen nach liefert zunächst $r={\frac {\varepsilon d}{1-\varepsilon \cos \varphi }}$ . Setzt man $p=r(\pi /2)=\varepsilon d$ , so erhält man die Polardarstellung der nichtausgearteten Kegelschnitte:

$r={\frac {p}{1-\varepsilon \cos \varphi }}$ .

ist dabei der Halbparameter (halbe Breite des Kegelschnitts am Brennpunkt) und $\varepsilon$ die numerische Exzentrizität. Wählt man den Halbparameter fest, so erhält man Kegelschnitte mit dem Nullpunkt als gemeinsamen Brennpunkt, und zwar

für $\varepsilon=0$ den Kreis mit Mittelpunkt $M=(0,0)$ und Radius $R=p$ ,

für $0<\varepsilon <1$ die Ellipse mit dem Mittelpunkt $M=(e,0),\ e={\frac {p\;\varepsilon }{1-\varepsilon ^{2}}}$ und den Halbachsen $a={\frac {e}{\varepsilon }},\ b={\sqrt {a^{2}-e^{2}}}$ ,

für $\varepsilon =1$ die Parabel mit dem Scheitel $S=(-{\frac {p}{2}},0)$ und der Gleichung $x={\frac {y^{2}-p^{2}}{2p}}$ ,

für $\varepsilon>1$ die Hyperbel mit dem Mittelpunkt $M=(-e,0),\ e={\frac {p\;\varepsilon }{\varepsilon ^{2}-1}}$ und den Halbachsen $a={\frac {e}{\varepsilon }},\ b={\sqrt {e^{2}-a^{2}}}$ .

Kegelschnittbüschel

Sind die Gleichungen $f_{1}(x,y)=0,\ f_{2}(x,y)=0$ zweier Kegelschnitte gegeben, so lassen sich durch die Linearkombination

$a_{1}f_{1}(x,y)+a_{2}f_{2}(x,y)=0$

der Gleichungen neue Kegelschnitte erzeugen. Da proportionale Paare $(a_{1},a_{2})$ und $(ta_{1},ta_{2})$ äquivalente Gleichungen ergeben und daher zum selben Kegelschnitt gehören, schreibt man die Linearkombination oft so:

$(1-\mu )f_{1}(x,y)-\mu f_{2}(x,y)=0$

Kreisbüschel zu zwei vorgegebenen Kreisen (rot)

Kegelschnittbüschel zu 3 Geraden (rot: Kreis für $\mu ={\tfrac {5}{9}}$ , magenta: Ellipse, blau: Parabel für $\mu ={\tfrac {1}{5}}$ , grün: Hyperbel)

Kegelschnitt-Büschel durch 4 Punkte

Diese Gleichung beschreibt in eindeutiger Weise durch den Parameter $\mu$ jeweils einen Kegelschnitt.

Beispiel Kreisbüschel:

Für die zwei Kreisgleichungen

$f_{1}(x,y)=(x-2)^{2}+y^{2}-1=0$

$f_{2}(x,y)=(x+2)^{2}+y^{2}-1=0$

beschreibt $(1-\mu )f_{1}(x,y)-\mu f_{2}(x,y)=0$ mit $\mu \neq 1/2$ ein Büschel von Kreisen (s. Bild). (Für $\mu =1/2$ heben sich die quadratischen Terme auf und es ergibt sich die Gerade x=0 .)

Beispiel Kegelschnittbüschel durch 2 Punkte mit vorgegebenen Tangenten:

Das folgende Beispiel baut aus 3 Geraden $g_{1},g_{2},g_{3}$ ein Büschel von Kegelschnitten auf. Es sei:

$g_{0}:f_{0}(x,y)=y=0$

$g_{1}:f_{1}(x,y)=y/2-x-1=0$

$g_{2}:f_{2}(x,y)=y/2+x-1=0$

Dann beschreibt die Gleichung

$(1-\mu )f_{1}(x,y)\cdot f_{2}(x,y)-\mu f_{0}(x,y)^{2}=0$

mit dem Scharparameter $\mu$ ein Büschel von Kegelschnitten durch die beiden Punkte $P_{1}=g_{0}\cap g_{1}$ und $P_{2}=g_{0}\cap g_{2}$ . Jeder Kegelschnitt berührt die beiden Geraden $g_{1},g_{2}$ in diesen Punkten. Das Kegelschnittbüschel ist also durch die beiden Punkte P_1, P_2 und die beiden Tangenten $g_{1},g_{2}$ in diesen Punkten bestimmt. (Ein Kegelschnitt ist immer durch 5 Vorgaben eindeutig bestimmt!) Beide Kegelschnitte, mit der die Linearkombination gebildet wird, sind ausgeartete Kegelschnitte ( $f_{1}f_{2}=0$ ist ein Geradenpaar und $f_{0}^{2}=0$ ist eine Doppelgerade).

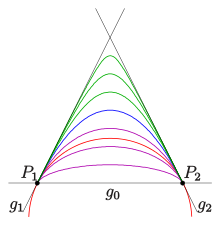
Beispiel Kegelschnittbüschel durch 4 Punkte:

In diesem Fall ist das Büschel eine Linearkombination zweier paralleler Geradenpaare, die sich in den 4 Punkten $(\pm 1,\pm 1)$ schneiden (s. Bild):

$a_{1}(x^{2}-1)+a_{2}(y^{2}-1)=0$

Durch jeden Punkt der Ebene, der von den Grundpunkten des Büschels verschieden ist, geht genau ein (eventuell ausgearteter) Kegelschnitt des Büschels. Z.B. erhält man zum Nullpunkt (0,0) für $a_{1}=1,a_{2}=-1$ das Geradenpaar $y^{2}=x^{2}$ .

Kegelschnittbüschel werden in der Literatur ausführlich untersucht.

Äquivalenz nicht ausgearteter Kegelschnitte

Alle Ellipsen sind affine Bilder des Einheitskreises (s. Ellipse).
Alle Parabeln sind affine Bilder der Normalparabel (s. Parabel).
Alle Hyperbeln sind affine Bilder der Einheitshyperbel (s. Hyperbel).

Eine Ellipse ist aber mit einer affinen Abbildung nicht (z.B.) auf eine Parabel abbildbar. Ergänzt man aber die affine Koordinatenebene zu einer projektiven Ebene und fügt einer Parabel den Fernpunkt ihrer Achse hinzu, so lässt sich eine Ellipse mit einer projektiven Abbildung auf eine so erweiterte Parabel abbilden. Das Analoge gilt für eine um die zwei Fernpunkte ihrer Asymptoten ergänzte Hyperbel.

Vom projektiven Standpunkt aus sind also alle nicht ausgearteten projektiven Kegelschnitte zueinander äquivalent (s. auch Weblink CDKG, S. 251).

Beispiele:

Die projektive Abbildung mit $(x,y)\to (\tfrac{x}{1+y},\tfrac{1-y}{1+y})$ bildet den Einheitskreis auf die Parabel ab.
Die projektive Abbildung mit $(x,y)\to (\tfrac{1}{x},\tfrac{y}{x})$ bildet die Parabel auf die Hyperbel $y=\tfrac{1}{x}$ ab.

Anwendungen und Beispiele

Kegelschnitte beschreiben die Bahnen von Himmelskörpern

Kegelschnitt in der Architektur: Kathedrale von Brasilia

Eine Anwendung finden die Kegelschnitte in der Astronomie, da die Bahnen der Himmelskörper genäherte Kegelschnitte sind.

Auch in der Optik werden sie verwendet – als Rotationsellipsoid für Autoscheinwerfer, als Paraboloid oder Hyperboloid für Spiegelteleskope usw.

Geschichte

Der griechische Mathematiker Menaichmos untersuchte an Platons Akademie die Kegelschnitte mit Hilfe eines Kegelmodells. Er fand dabei heraus, dass sich das delische Problem auf die Bestimmung des Schnittpunkts zweier Kegelschnitte zurückführen lässt. Danach behandelte Aristaios von Samos (Aristaios der Ältere) in einem nicht mehr erhaltenen Buch das Problem der Konstruktion von Kegelschnitten in Bezug auf drei oder vier Geraden, was später in der Begründung der analytischen Geometrie von René Descartes wieder aufgenommen wurde. Euklid schrieb vier Bücher über Kegelschnitte, die uns aber nicht erhalten sind. Die gesamten Kenntnisse der antiken Mathematiker über die Kegelschnitte fasste Apollonios von Perge in seinem achtbändigen Werk Konika zusammen, wobei Apollonios wie Euklid den synthetischen Zugang zur Geometrie bevorzugte. Die Werke von Euklid, Apollonios und Aristaios wurden ab der Renaissance in Westeuropa wieder aufgegriffen und weiterentwickelt. Die Beschreibung von Kegelschnitten durch Koordinatengleichungen wurde von Fermat und Descartes eingeführt.

Kegelschnitte über beliebigen Zahl-Körpern

Kegelschnitte lassen sich auch über beliebigen Körpern definieren. Es bleiben dabei erstaunlich viele Inzidenz- und Symmetrieeigenschaften erhalten. Siehe projektiver Kegelschnitt und für Kegelschnitte über endlichen Körpern den Artikel Quadratische Menge.

Kegelschnitte und Benz-Ebenen

Kegelschnitte spielen bei den Benz-Ebenen, das sind Möbius-Ebenen (Geometrie der Kreise), Laguerre-Ebenen (Geometrie der Parabeln) und Minkowski-Ebenen (Geometrie der Hyperbeln), eine wichtige Rolle.

Siehe auch

Literatur

Max Koecher, Aloys Krieg: Ebene Geometrie. 3. Aufl., Springer-Verlag, Berlin 2007, ISBN 978-3-540-49327-3.
Burg, Haf, Wille: Höhere Mathematik für Ingenieure. Band II, Teubner-Verlag Stuttgart, ISBN 3-519-22956-0.

Basierend auf einem Artikel in:

Wikipedia.de