Hyperboloid

Einschaliges Hyperboloid

Zweischaliges Hyperboloid

Ein Hyperboloid ist im einfachsten Fall eine Fläche, die durch Rotation einer Hyperbel um eine ihrer Achsen entsteht.

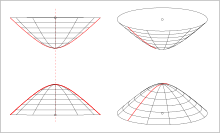
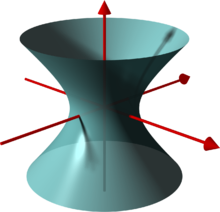
Bei Rotation einer Hyperbel um ihre Nebenachse entsteht ein einschaliges Hyperboloid. Es besteht aus einem zusammenhängenden Flächenstück.
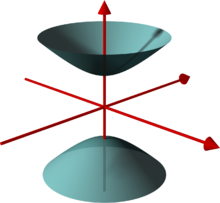
Bei Rotation einer Hyperbel um ihre Hauptachse entsteht ein zweischaliges Hyperboloid. Es besteht aus zwei getrennten Flächenstücken.

Beide Flächen lassen sich durch eine quadratische Gleichung – analog zu den Gleichungen von Ellipse und Hyperbel – beschreiben. Sie sind deshalb Spezialfälle von Quadriken (z. B. Kugel, Kegel, Paraboloid) und werden typischerweise von Ebenen in Kegelschnitten geschnitten.

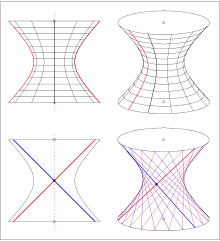
Ein wesentlicher Unterschied zwischen einem einschaligen und einem zweischaligen Hyperboloid ist, dass das einschalige Hyperboloid Geraden enthält, es also eine Regelfläche ist, das zweischalige nicht.

Diese Eigenschaft macht das einschalige Hyperboloid für Architekten und Bauingenieure interessant, da sich einschalige Hyperboloide leicht aus Geraden modellieren lassen. Einige Kühltürme haben die Form eines einschaligen Hyperboloids. Auch im Maschinenbau finden einschalige Hyperboloide Verwendung bei Hyperboloidgetrieben, Einschalige Hyperboloide spielen auch in der synthetischen Geometrie eine Rolle: Eine Minkowski-Ebene ist die Geometrie der ebenen Schnitte eines einschaligen Hyperboloids. Während das einschalige Hyperboloid von Tangentialebenen in zwei sich schneidenden Geraden geschnitten wird (siehe unten), hat ein zweischaliges Hyperboloid mit Tangentialebenen immer nur einen Punkt gemeinsam und ist deshalb geometrisch mehr mit einer Kugel verwandt.

Eigenschaften

Einschaliges Einheitshyperboloid

Einschaliges Hyperboloid: Erzeugung durch Rotation einer Hyperbel (oben) bzw. einer Geraden (unten: rot oder blau)

Einschaliges Hyperboloid: ebene Schnitte

Lässt man die Hyperbel $x^{2}-z^{2}=1$ in der x-z-Ebene um die z-Achse rotieren (siehe Abbildung), so erhält man das einschalige Einheits-Hyperboloid mit der Gleichung

$H_{1}\colon \ x^{2}+y^{2}-z^{2}=1$ .

Bei der Rotation wird $x^{2}$ durch $x^{2}+y^{2}$ ersetzt.

Das einschalige Einheits-Hyperboloid ergibt sich durch Rotation des Graphen der Funktion $f(z)={\sqrt {z^{2}+1}}$ um die -Achse. Für die Ableitung gilt $f'(z)={\frac {z}{\sqrt {z^{2}+1}}}$ . Das Volumen und die Oberfläche für ein einschalige Einheits-Hyperboloid mit der Höhe ergeben sich nach den Guldinschen Regeln mithilfe von Integralen.

Rotationsparaboloid mit Parabeln und Höhenkreisen

Volumen

$V=\pi \int _{0}^{h}(f(z))^{2}\ \mathrm {d} z=\pi \int _{0}^{h}z^{2}+1\ \mathrm {d} z=\pi \left({\frac {h^{3}}{3}}+h\right)={\frac {\pi }{3}}\left(h^{3}+3h\right)$

Oberfläche

${\begin{aligned}A&=2\pi \int _{0}^{h}f(z){\sqrt {1+\left(f'(z)\right)^{2}}}\ \mathrm {d} z\\&=2\pi \int _{0}^{h}{\sqrt {z^{2}+1}}{\sqrt {1+\left({\frac {z}{\sqrt {z^{2}+1}}}\right)^{2}}}\ \mathrm {d} z\\&=2\pi \int _{0}^{h}{\sqrt {2z^{2}+1}}\ \mathrm {d} z\\&=2\pi \left({\frac {1}{2}}z{\sqrt {2z^{2}+1}}+{\frac {\sqrt {2}}{2}}\ln \left({\sqrt {2}}z+{\sqrt {2z^{2}+1}}\right){\Big |}_{z=0}^{z=h}\right)\\&=\pi \left(h{\sqrt {2h^{2}+1}}+{\sqrt {2}}\ln \left({\sqrt {2}}h+{\sqrt {2h^{2}+1}}\right)\right)\end{aligned}}$

Parameterdarstellung

Offensichtlich ist jeder Höhenschnitt mit einer Ebene $z=z_{0}$ ein Kreis mit Radius ${\sqrt {1+z_{0}^{2}}}$ . Der Schnitt der Ebene x=1 liefert die beiden Schnittgeraden $(1,t,\pm t)^{\top },t\in \mathbb {R}$ . Durch Rotation dieser Geraden erhält man Parameterdarstellungen aller Geraden auf dem Hyperboloid:

$g_{\alpha }^{\pm }:{\vec {x}}(t)={\begin{pmatrix}\cos \alpha \\\sin \alpha \\0\end{pmatrix}}+t\cdot {\begin{pmatrix}-\sin \alpha \\\cos \alpha \\\pm 1\end{pmatrix}}\ ,\quad t\in \mathbb {R} ,\ 0\leq \alpha \leq 2\pi$

Das einschalige Hyperboloid $H_{1}$ lässt sich also auch durch Rotation der Geraden $g_{0}^{+}$ oder $g_{0}^{-}$ (windschief zur Rotationsachse) erzeugen (siehe Abbildung). Diese Aussage wird in der Literatur als Satz von Wren bezeichnet.

Tangentialebenen

Die Gleichung der Tangentialebene einer implizit durch f(x,y,z)=0 gegebenen Fläche in einem Punkt ${\vec {x}}_{0}=(x_{0},y_{0},z_{0})$ ist $f_{x}({\vec {x}}_{0})(x-x_{0})+f_{y}({\vec {x}}_{0})(y-y_{0})+f_{z}({\vec {x}}_{0})(z-z_{0})=0$ .

Für H1 ergibt sich

$x_{0}x+y_{0}y-z_{0}z-1=0\ .$

Ebene Schnitte

Ebenen mit einer Neigung kleiner 1 (1 ist die Neigung der Geraden auf dem Hyperboloid) schneiden $H_{1}$ in einer Ellipse,
Ebenen mit einer Neigung gleich 1 durch den Koordinatenursprung schneiden $H_{1}$ in einem parallelen Geradenpaar,
Ebenen mit einer Neigung gleich 1 nicht durch den Koordinatenursprung schneiden $H_{1}$ in einer Parabel,
Tangentialebenen schneiden $H_{1}$ in einem sich schneidenden Geradenpaar,
Ebenen mit einer Neigung größer 1, die keine Tangentialebenen sind, schneiden $H_{1}$ in einer Hyperbel.

Eine Ebene, die eine Hyperboloid-Gerade enthält, ist entweder eine Tangentialebene und enthält damit eine zweite schneidende Hyperboloid-Gerade oder enthält eine zu parallele Hyperboloid-Gerade und ist damit Tangentialebene in einem Fernpunkt.

Affine Bilder

Analog wie eine beliebige Ellipse als affines Bild des Einheitskreises aufgefasst werden kann, ist ein beliebiges einschaliges Hyperboloid das affine Bild des Einheitshyperboloids $H_{1}$ . Die einfachsten affinen Bilder erhält man durch Skalierung der Koordinatenachsen:

${\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}-{\frac {z^{2}}{c^{2}}}=1\ ,\ a,b,c>0.$

Im Fall a=b sind die Höhenschnitte Kreise. Andern falls sind es Ellipsen. Ein solches Hyperboloid nennt man einschaliges Rotationshyperboloid. Dass ein beliebiges einschaliges Hyperboloid auch immer Kreise enthält, wird in Kreisschnittebene gezeigt.

Da ein beliebiges einschaliges Hyperboloid Geraden enthält, ist es eine Regelfläche. Da jede Tangentialebene eines einschaligen Hyperboloids in der Nähe seines Berührpunktes die Fläche schneidet, hat es eine negative Gaußsche Krümmung und ist deswegen nicht abwickelbar, im Gegensatz zu den Regelflächen Kegel und Zylinder, die die Gaußsche Krümmung 0 haben. Aus der üblichen Parameterdarstellung einer Hyperbel mit Hyperbelfunktionen erhält man die folgende Parameterdarstellung des Hyperboloids ${\tfrac {x^{2}}{a^{2}}}+{\tfrac {y^{2}}{b^{2}}}-{\tfrac {z^{2}}{c^{2}}}=1:$

${\vec {x}}(s,t)=\left({\begin{array}{lll}a\cosh s\cos t\\b\cosh s\sin t\\c\sinh s\end{array}}\right),\quad s\in \mathbb {R} ,\ 0\leq t\leq 2\pi$

Homogene Koordinaten

Führt man homogene Koordinaten so ein, dass die Fernebene durch die Gleichung $x_{4}=0$ beschrieben wird, muss man $x={\tfrac {x_{1}}{x_{4}}},y={\tfrac {x_{2}}{x_{4}}},z={\tfrac {x_{3}}{x_{4}}}$ setzen. Nach Beseitigung des Nenners erhält man die homogene Beschreibung von $H_{1}$ durch die Gleichung:

$x_{1}^{2}+x_{2}^{2}-x_{3}^{2}-x_{4}^{2}=0$ .

Der Schnitt des Hyperboloids mit der Fernebene $x_{4}=0$ ist ein Kreis.
Die Umformung zu $(x_{1}-x_{3})(x_{1}+x_{3})+(x_{2}-x_{4})(x_{2}+x_{4})=0$ und anschließende Einführung neuer Koordinaten $u_{1}=x_{1}-x_{2},\;u_{2}=x_{1}+x_{3},\;u_{3}=x_{2}-x_{4},\;u_{4}=x_{2}+x_{4}\;$ liefert die Beschreibung des einschaligen Hyperboloids in homogenen Koordinaten durch die Gleichung

$u_{1}u_{2}+u_{3}u_{4}=0\ .$

In den neuen Koordinaten schneidet die Ebene $u_{4}=0$ das Hyperboloid in zwei Geraden.
Führt man jetzt wieder affine Koordinaten durch $x={\tfrac {u_{1}}{u_{4}}},y={\tfrac {u_{2}}{u_{4}}},z={\tfrac {u_{3}}{u_{4}}}$ ein, erhält man die Gleichung eines hyperbolischen Paraboloids:

$z=-xy\ .$

Dies zeigt: Ein einschaliges Hyperboloid ist projektiv äquivalent zu einem hyperbolischen Paraboloid.

Zweischaliges Hyperboloid

Zweischaliges Einheitshyperboloid

Zweischaliges Hyperboloid: Erzeugung durch Rotation einer Hyperbel

Zweischaliges Hyperboloid: ebene Schnitte

Lässt man die Hyperbel $-x^{2}+z^{2}=1$ in der x-z-Ebene um die z-Achse rotieren (siehe Abbildung), so erhält man das zweischalige Einheits-Hyperboloid mit der Gleichung $-x^{2}-y^{2}+z^{2}=1$ oder in üblicher Form

$H_{2}\colon \ x^{2}+y^{2}-z^{2}=-1$ .

Der Schnitt der Ebene $z=z_{0}$ mit $H_{2}$ ist ein Kreis (falls $z_{0}^{2}>1$ ) oder ein Punkt (falls $z_{0}=\pm 1$ ) oder leer (falls $z_{0}^{2}<1$ ). $H_{2}$ besteht aus zwei Teilen, entsprechend den zwei Teilen der Hyperbel.

Das zweischalige Einheits-Hyperboloid ergibt sich durch Rotation des Graphen der Funktion $f(z)={\sqrt {z^{2}-1}}$ um die -Achse. Für die Ableitung gilt $f'(z)={\frac {z}{\sqrt {z^{2}-1}}}$ . Das Volumen und die Oberfläche für ein zweischalige Einheits-Hyperboloid mit der Höhe $h-1$ ergeben sich nach den Guldinschen Regeln mithilfe von Integralen.

Volumen

$V=\pi \int _{1}^{h}(f(z))^{2}\ \mathrm {d} z=\pi \int _{1}^{h}z^{2}-1\ \mathrm {d} z=\pi \left({\frac {h^{3}}{3}}-h+{\frac {2}{3}}\right)={\frac {\pi }{3}}\left(h^{3}-3h+2\right)$

Oberfläche

${\begin{aligned}A&=2\pi \int _{0}^{h}f(z){\sqrt {1+\left(f'(z)\right)^{2}}}\ \mathrm {d} z\\&=2\pi \int _{0}^{h}{\sqrt {z^{2}-1}}{\sqrt {1+\left({\frac {z}{\sqrt {z^{2}-1}}}\right)^{2}}}\ \mathrm {d} z\\&=2\pi \int _{0}^{h}{\sqrt {2z^{2}-1}}\ \mathrm {d} z\\&=2\pi \left({\frac {1}{2}}z{\sqrt {2z^{2}-1}}-{\frac {\sqrt {2}}{2}}\ln \left({\sqrt {2}}z+{\sqrt {2z^{2}-1}}\right){\Big |}_{z=0}^{z=h}\right)\\&=\pi \left(h{\sqrt {2h^{2}-1}}-{\sqrt {2}}\ln \left({\sqrt {2}}h+{\sqrt {2h^{2}-1}}\right)\right)\end{aligned}}$

Tangentialebenen

Die Tangentialebene von $H_{2}$ in einem Punkt $(x_{0},y_{0},z_{0})$ hat die Gleichung (siehe oben)

$x_{0}x+y_{0}y-z_{0}z+1=0\ .$

Ebene Schnitte

Ebenen mit einer Neigung kleiner 1 (Neigung der Asymptoten der erzeugenden Hyperbel) schneiden $H_{2}$ entweder in einer Ellipse oder in einem Punkt oder nicht,
Ebenen mit einer Neigung gleich 1 und durch den Koordinatenursprung schneiden $H_{2}$ nicht,
Ebenen mit einer Neigung gleich 1 und nicht durch den Koordinatenursprung schneiden $H_{2}$ in einer Parabel,
Ebenen mit einer Neigung größer 1 schneiden $H_{2}$ in einer Hyperbel.

Affine Bilder

Ein beliebiges zweischaliges Hyperboloid ist das affine Bild des Einheitshyperboloids $H_{2}$ . Die einfachsten affinen Bilder erhält man durch Skalierung der Koordinatenachsen:

${\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}-{\frac {z^{2}}{c^{2}}}=-1\ ,\ a,b,c>0.$

Im Fall a=b sind die Höhenschnitte Kreise. Andern falls sind es Ellipsen. Ein solches Hyperboloid nennt man zweischaliges Rotationshyperboloid. Dass ein beliebiges zweischaliges Hyperboloid auch immer Kreise enthält, wird in Kreisschnittebene gezeigt.

Für ein zweischaliges Hyperboloid ${\tfrac {x^{2}}{a^{2}}}+{\tfrac {y^{2}}{b^{2}}}-{\tfrac {z^{2}}{c^{2}}}=-1$ ergibt sich die folgende Parameterdarstellung:

${\vec {x}}(s,t)=\left({\begin{array}{lll}a\sinh s\cos t\\b\sinh s\sin t\\\pm c\cosh s\end{array}}\right),\quad s\in \mathbb {R} ,\ 0\leq t\leq 2\pi$

Homogene Koordinaten

Führt man wie bei $H_{1}$ homogene Koordinaten ein, erhält man die homogene Beschreibung von $H_{2}$ durch die Gleichung:

$x_{1}^{2}+x_{2}^{2}-x_{3}^{2}+x_{4}^{2}=0$ .

Vertauscht man die Koordinaten $x_{3},x_{4}$ und kehrt wieder zu affinen Koordinaten zurück, ergibt sich die Gleichung der Einheitskugel:

$x^{2}+y^{2}+z^{2}=1\ .$

Dies zeigt: Ein zweischaliges Hyperboloid ist projektiv äquivalent zu einer Kugel.

Symmetrieeigenschaften

Wie Ellipsen und Hyperbeln haben auch Hyperboloide Scheitel und Nebenscheitel und Symmetrien. Die Hyperboloide ${\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}-{\frac {z^{2}}{c^{2}}}=1,\quad {\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}-{\frac {z^{2}}{c^{2}}}=-1\$ sind offensichtlich

punktsymmetrisch zum Koordinatenursprung,
symmetrisch zu den Koordinatenebenen sowie
rotationssymmetrisch zur z-Achse und symmetrisch zu jeder Ebene durch die z-Achse, falls ist.

Doppelkegel

Doppelkegel

Den Doppelkegel $x^{2}+y^{2}-z^{2}=0$ kann man als Grenzfläche zwischen den Scharen von einschaligen bzw. zweischaligen Hyperboloiden $x^{2}+y^{2}-z^{2}=c^{2}$ bzw. $x^{2}+y^{2}-z^{2}=-c^{2}$ auffassen. Er entsteht durch Rotation der gemeinsamen Asymptoten der Erzeuger-Hyperbeln.

Gemeinsame Parameterdarstellung

Es gibt verschiedene Möglichkeiten. Hyperboloide zu parametrisieren. Eine einfache Möglichkeit, das einschalige und zweischalige Hyperboloid und den Kegel zu parametrisieren, ist:

${\vec {x}}(s,t)=\left({\begin{array}{lll}a\ {\sqrt {s^{2}+d}}\ \cos t\\b\ {\sqrt {s^{2}+d}}\ \sin t\\cs\end{array}}\right)$

Für d=1 ergibt sich ein einschaliges, für d=-1 ein zweischaliges Hyperboloid und für d=0 ein Doppelkegel.

Wasserturm in Frankreich in Form eines einschaligen Hyperboloids

Hafenturm in Kobe (Japan) in Form eines einschaligen Hyperboloids

Siehe auch

Literatur

Albrecht Beutelspacher, Ute Rosenbaum: Projektive Geometrie. Von den Grundlagen bis zu den Anwendungen (= Vieweg Studium: Aufbaukurs Mathematik). 2., durchgesehene und erweiterte Auflage. Vieweg, Wiesbaden 2004, ISBN 3-528-17241-X.
Hermann Schaal: Lineare Algebra und analytische Geometrie. Band III. Vieweg, 1980, ISBN 3-528-13057-1.
Günter Scheja, Uwe Storch: Lehrbuch der Algebra. Unter Einschluß der linearen Algebra. 2., überarb. und erw. Auflage. Teubner, Stuttgart 1994, ISBN 3-519-12203-0.
Uwe Storch, Hartmut Wiebe: Lehrbuch der Mathematik. 2., überarb. und erw. Auflage. BI-Wissenschafts-Verlag, 1999, ISBN 3-411-14101-8.

Basierend auf einem Artikel in:

Wikipedia.de