Website durchsuchen

Regelfläche

Regelfläche: Definition

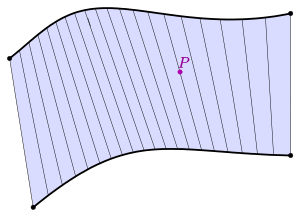
In der Geometrie heißt eine Fläche Regelfläche, wenn gilt

Einfache Beispiele sind Ebenen, Zylinder, Kegel und einschalige Hyperboloide. Bei einem einschaligen Hyperboloid gehen durch jeden Punkt sogar zwei Geraden. Allerdings gilt: Eine Regelfläche, bei der durch jeden Punkt drei Geraden gehen, kann nur eine Ebene sein.

Bei konkreten Regelflächen beschränkt man oft die Erzeugenden auf Strecken, um eine unendliche Ausdehnung (z.B. bei Zylindern oder Kegeln) oder Selbstdurchdringungen (z.B. bei Regelschraubflächen) zu vermeiden.

Im Begriff Regelfläche hat Regel – wie auch in Kippregel – die ursprüngliche Bedeutung des lateinischen regula (Stab, Lineal), die heute noch im englischen rule oder dem französischen règle enthalten ist.

Regelflächen finden in der Architektur als leicht modellierbare Flächen Anwendung. Z.B. hat ein Kühlturm oft die Form eines einschaligen Hyperboloids. Im Metallgewerbe werden abwickelbare Regelflächen, wie z.B. Zylinder und Kegel, verwendet. (Das einschalige Hyperboloid ist nicht abwickelbar!) Abwickelbare Flächen haben den praktischen Vorteil, dass man sie aus ihren Abwicklungen aus Blech durch Aufwickeln herstellen kann (s. Abwicklung (Darstellende Geometrie)). Bei der geometrischen Modellierung werden Regelflächen z.B. zur Erzeugung von Coons-Flächen verwendet.

Definition und Parameterdarstellung

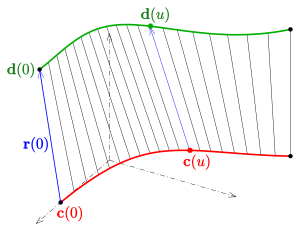
Regelfläche erzeugt mit zwei Bezierkurven als Leitkurven (rot, grün)

Definition

Parameterdarstellung Eine Regelfläche lässt sich durch eine Parameterdarstellung der Form

beschreiben. Jede Flächenkurve {\displaystyle \;\mathbf {x} (u_{0},v)\;} mit festem Parameter u=u_{0} ist eine Erzeugende (Gerade) und die Kurve {\displaystyle \;\mathbf {c} (u)\;} ist die Leitkurve. Die Vektoren {\displaystyle \;\mathbf {r} (u)\;} beschreiben das Richtungsfeld der Erzeugenden.

Die durch die Parameterdarstellung * beschriebene Regelfläche, kann man auch mit Hilfe der Kurve {\displaystyle \;\mathbf {d} (u)=\mathbf {c} (u)+\mathbf {r} (u)\;} als zweite Leitkurve beschreiben:

Umgekehrt kann man von zwei sich nicht schneidenden Kurven als Leitkurven ausgehen und erhält damit die Darstellung einer Regelfläche mit dem Richtungsfeld {\displaystyle \;\mathbf {r} (u)=\mathbf {d} (u)-\mathbf {c} (u)\ .}

Bei der Erzeugung einer Regelfläche mit Hilfe zweier Leitkurven (oder einer Leitkurve und eines Richtungsfeldes) ist nicht nur die geometrische Gestalt dieser Kurven von Bedeutung, sondern die konkrete Parameterdarstellung hat wesentlichen Einfluss auf die Gestalt der Regelfläche. Siehe Beispiele d)

Für theoretische Untersuchungen (s.u.) ist die Darstellung (CR) vorteilhaft, da der Parameter v nur in einem Term vorkommt.

Beispiele

Regelflächen: Zylinder, Kegel

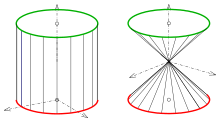
a) Senkrechter Kreiszylinder {\displaystyle \ x^{2}+y^{2}=a^{2}\ }:

{\displaystyle \mathbf {x} (u,v)=(a\cos u,a\sin u,v)^{T}}
{\displaystyle ={\color {red}(a\cos u,a\sin u,0)^{T}}\;+\;v\;{\color {blue}(0,0,1)^{T}}}
{\displaystyle =(1-v)\;{\color {red}(a\cos u,a\sin u,0)^{T}}\;+\;v\;{\color {green}(a\cos u,a\sin u,1)^{T}}\ .}

Hierbei ist {\displaystyle \quad \mathbf {c} (u)=(a\cos u,a\sin u,0)^{T}\ ,\quad \mathbf {r} (u)=(0,0,1)^{T}\ ,\quad \mathbf {d} (u)=(a\cos u,a\sin u,1)^{T}\ .}

b) Senkrechter Kreiskegel {\displaystyle \ x^{2}+y^{2}=z^{2}\ }:

{\displaystyle \mathbf {x} (u,v)=(\cos u,\sin u,1)^{T}\;+\;v\;(\cos u,\sin u,1)^{T}}
{\displaystyle =(1-v)\;(\cos u,\sin u,1)^{T}\;+\;v\;(2\cos u,2\sin u,2)^{T}.}

Hier ist {\displaystyle \quad \mathbf {c} (u)=(\cos u,\sin u,1)^{T}\;=\;\mathbf {r} (u)\ ,\quad \mathbf {d} (u)=(2\cos u,2\sin u,2)^{T}\ .}
Man hätte auch als Leitkurve {\displaystyle \ \mathbf {c} (u)=(0,0,0)^{T}\ }, also die Spitze des Kegels, und als Richtungsfeld {\displaystyle \ \mathbf {r} (u)=(\cos u,\sin u,1)^{T}\ } wählen können. Bei allen Kegeln kann man als Leitkurve die Spitze wählen.

Wendelfläche als Regelfläche

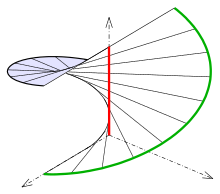
c) Wendelfläche:

{\displaystyle \mathbf {x} (u,v)=\;(v\cos u,v\sin u,ku)^{T}\;}
{\displaystyle =\;(0,0,ku)^{T}\;+\;v\;(\cos u,\sin u,0)^{T}\ }
{\displaystyle =\;(1-v)\;(0,0,ku)^{T}\;+\;v\;(\cos u,\sin u,ku)^{T}\ .}

Die Leitkurve {\displaystyle \ \mathbf {c} (u)=(0,0,ku)^{T}\;} ist die z-Achse, das Richtungsfeld {\displaystyle \;\mathbf {r} (u)=\ (\cos u,\sin u,0)^{T}\;} und die zweite Leitkurve {\displaystyle \ \mathbf {d} (u)=(\cos u,\sin u,ku)^{T}\ } ist eine Schraublinie.

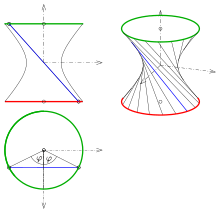
Regelfläche: einschaliges Hyperboloid für {\displaystyle \varphi =63^{\circ }}

d) Zylinder, Kegel und Hyperboloide:
Die Parameterdarstellung

{\displaystyle \mathbf {x} (u,v)=(1-v)\;(\cos(u-\varphi )\;,\;\sin(u-\varphi )\;,\;-1)^{T}\;+\;v\;(\cos(u+\varphi )\;,\;\sin(u+\varphi )\;,\;1)^{T}}

besitzt zwei horizontale Einheitskreise als Leitkurven. Der zusätzliche Parameter \varphi erlaubt es, die Parametrdarstellungen der Kreise zu variieren. Für

{\displaystyle \varphi =0\ } erhält man den Zylinder x^2+y^2=1, für
{\displaystyle \varphi =\pi /2\ } erhält man den Kegel x^2+y^2=z^2 und für
{\displaystyle 0<\varphi <\pi /2\ } erhält man ein einschaliges Hyperboloid mit der Gleichung {\displaystyle \ {\tfrac {x^{2}+y^{2}}{a^{2}}}-{\tfrac {z^{2}}{c^{2}}}=1\ } und den Halbachsen {\displaystyle \ a=\cos \varphi \;,\;c=\cot \varphi }.
Hyperbolisches Paraboloid

e) Hyperbolisches Paraboloid:

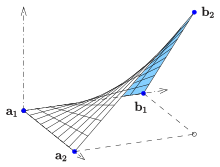
Falls die Leitlinien in (CD) die Geraden

{\displaystyle \mathbf {c} (u)=(1-u)\mathbf {a} _{1}+u\mathbf {a} _{2},\quad \mathbf {d} (u)=(1-u)\mathbf {b} _{1}+u\mathbf {b} _{2}}

sind, erhält man

{\displaystyle \mathbf {x} (u,v)=(1-v){\big (}(1-u)\mathbf {a} _{1}+u\mathbf {a} _{2}{\big )}\ +\ v{\big (}(1-u)\mathbf {b} _{1}+u\mathbf {b} _{2}{\big )}\ }.

Dies ist das hyperbolische Paraboloid, das die 4 Punkte {\displaystyle \ \mathbf {a} _{1},\;\mathbf {a} _{2},\;\mathbf {b} _{1},\;\mathbf {b} _{2}\ } bilinear interpoliert. Für das Beispiel der Zeichnung ist

{\displaystyle \ \mathbf {a} _{1}=(0,0,0)^{T},\;\mathbf {a} _{2}=(1,0,0)^{T},\;\mathbf {b} _{1}=(0,1,0)^{T},\;\mathbf {b} _{2}=(1,1,1)^{T}\ }.

und das hyperbolische Paraboloid hat die Gleichung {\displaystyle z=xy}.

Möbiusband

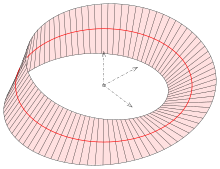
f) Möbiusband:

Die Regelfläche

{\displaystyle \mathbf {x} (u,v)=\mathbf {c} (u)+v\;\mathbf {r} (u)}

mit

{\displaystyle \mathbf {c} (u)=(\cos 2u,\sin 2u,0)^{T}\ } (die Leitkurve ist ein Kreis),
{\displaystyle \mathbf {r} (u)=(\cos u\cos 2u,\cos u\sin 2u,\sin u)^{T}\ ,\quad 0\leq u<\pi \ ,}

enthält ein Möbiusband.

Die Zeichnung zeigt das Möbiusband für {\displaystyle -0.3\leq v\leq 0.3}.

Man rechnet leicht nach, dass {\displaystyle \det(\mathbf {\dot {c}} (0)\;,\;\mathbf {\dot {r}} (0)\;,\;\mathbf {r} (0))\;\neq \;0\ } ist (s. nächsten Abschnitt). D.h. diese Realisierung eines Möbiusbandes ist nicht abwickelbar. Es gibt allerdings auch abwickelbare Möbiusbänder.

Tangentialebenen, abwickelbare Flächen

Für die hier notwendigen Ableitungen wird stets vorausgesetzt, dass sie auch existieren.

Um den Normalenvektor in einem Punkt zu berechnen, benötigt man die partiellen Ableitungen der Darstellung {\displaystyle \quad \mathbf {x} (u,v)=\mathbf {c} (u)+v\;\mathbf {r} (u)} :

{\displaystyle \mathbf {x} _{u}=\mathbf {\dot {c}} (u)+v\;\mathbf {\dot {r}} (u)\ } ,{\displaystyle \quad \mathbf {x} _{v}=\;\mathbf {r} (u)}

Da das Skalarprodukt {\displaystyle \mathbf {n} \cdot \mathbf {r} =0} ist (Ein Spatprodukt mit zwei gleichen Vektoren ist immer 0!), ist {\displaystyle \mathbf {r} (u_{0})} ein Tangentenvektor in jedem Punkt {\mathbf x}(u_{0},v). Die Tangentialebenen entlang dieser Gerade sind identisch, falls {\displaystyle \mathbf {\dot {r}} \times \mathbf {r} } ein Vielfaches von {\displaystyle \mathbf {\dot {c}} \times \mathbf {r} } ist. Dies ist nur möglich, wenn die drei Vektoren {\displaystyle \mathbf {\dot {c}} \;,\;\mathbf {\dot {r}} \;,\;\mathbf {r} \ } in einer Ebene liegen, d.h. linear abhängig sind. Die lineare Abhängigkeit dreier Vektoren kann man mit Hilfe der Determinante dieser Vektoren feststellen:

{\displaystyle \det(\mathbf {\dot {c}} (u_{0})\;,\;\mathbf {\dot {r}} (u_{0})\;,\;\mathbf {r} (u_{0}))\;=\;0\ .}
Eine Erzeugende, für die dies gilt heißt torsal.
{\displaystyle \det(\mathbf {\dot {c}} \;,\;\mathbf {\dot {r}} \;,\;\mathbf {r} )\;=\;0\quad }
in jedem Punkt gilt, d.h., wenn jede Erzeugende eine Torsale ist. Eine abwickelbare Fläche heißt deswegen auch Torse.

Eigenschaften einer abwickelbaren Fläche:

Anwendung und Geschichte abwickelbarer Flächen

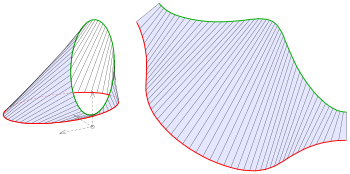
Verbindungstorse zweier Ellipsen und ihre Abwicklung

Die Determinantenbedingung für abwickelbare Flächen gibt einem eine Möglichkeit, eine Verbindungstorse zwischen zwei gegebenen Leitkurven numerisch zu ermitteln. Das Bild zeigt ein Beispiel einer Anwendung: Verbindungstorse zwischen zwei Ellipsen (eine horizontal, die andere vertikal) und ihre Abwicklung.

Einen Einblick in die Verwendung von abwickelbaren Flächen im CAD-Bereich findet man in Interactive design of developable surfaces

Einen historischen Überblick über abwickelbare Flächen gibt Developable Surfaces: Their History and Application

Weitere Beispiele

  1. Die Einhüllende einer einparametrigen Ebenenschar
  2. Hyperbolisches Paraboloid
  3. Oloid
  4. Catalansche Fläche
  5. Konoid
  6. Regelschraubflächen

Striktionslinie oder Kehllinie

Definition

Bei einer zylindrischen Regelfläche sind alle Erzeugenden parallel, d.h. alle Richtungsvektoren {\mathbf r}(u) sind parallel und damit {\displaystyle {\dot {\mathbf {r} }}(u)=\mathbf {0} \ .} Bei zwei parallelen Geraden haben alle Punkte der einen Gerade denselben Abstand zur anderen Gerade.

Bei einer nichtzylindrischen Regelfläche sind benachbarte Erzeugenden windschief und es existiert ein Punkt auf der einen Gerade, der minimalen Abstand zu der anderen Gerade hat. In diesem Fall ist {\displaystyle {\dot {\mathbf {r} }}(u)\neq \mathbf {0} \ .} Solch einen Punkt nennt man Zentralpunkt. Die Gesamtheit der Zentralpunkte bilden eine Kurve, die Striktionslinie oder Kehllinie oder auch Taille. Letztere Bezeichnung beschreibt sehr anschaulich die Striktionslinie eines einschaligen Rotations-Hyperboloids (s.u.).

Eine zylindrische Fläche besitzt keine Zentralpunkte und damit keine Striktionslinie, oder anschaulich: keine Taille. Bei einer (allgemeinen) Kegelfläche entartet die Striktionslinie/Taille zu einem Punkt, die Kegelspitze.

Parameterdarstellung

In den folgenden Überlegungen wird vorausgesetzt, dass die Regelfläche

{\displaystyle \mathbf {x} (u,v)=\mathbf {c} (u)+v\;\mathbf {r} (u)}

nicht zylindrisch und genügend differenzierbar ist, genauer:

{\displaystyle {\dot {\mathbf {r} }}(u)\neq \mathbf {0} \quad } und der Einfachheit halber {\displaystyle \quad |\mathbf {r} (u)|=1\ } ist.

Die letzte Eigenschaft hat den Vorteil, dass {\displaystyle \quad \mathbf {r} \cdot {\dot {\mathbf {r} }}=0\quad } ist, was Rechnungen stark vereinfacht. Bei konkreten Beispielen ist diese Eigenschaft meist zunächst nicht erfüllt. Was sich aber durch Normierung korrigieren lässt.

Zwei benachbarte Erzeugenden
{\displaystyle \mathbf {x} (v_{1})=\mathbf {c} (u)+v_{1}\;\mathbf {r} (u)}
{\displaystyle \mathbf {x} (v_{2})=\mathbf {c} (u+\Delta u)+v_{2}\;\mathbf {r} (u+\Delta u)}

Am Ende der Überlegungen geht dann {\displaystyle \Delta u\to 0}. Deshalb sind die folgenden linearen Approximationen (man ersetzt die Kurve in der näheren Umgebung durch ihre Tangente) sinnvoll:

{\displaystyle \mathbf {c} (u+\Delta u)\approx \mathbf {c} (u)+\Delta u\;{\dot {\mathbf {c} }}(u)}
{\displaystyle \mathbf {r} (u+\Delta u)\approx \mathbf {r} (u)+\Delta u\;{\dot {\mathbf {r} }}(u)}.
Abstandsquadrat

Das Quadrat des Abstandes zweier Punkte der Geraden

{\displaystyle \mathbf {l} _{1}(v_{1})=\mathbf {c} +v_{1}\;\mathbf {r} }
{\displaystyle \mathbf {l} _{2}(v_{2})=\mathbf {c} +\Delta u\;{\dot {\mathbf {c} }}+v_{2}\;(\mathbf {r} +\Delta u\;{\dot {\mathbf {r} }})\quad } ist
{\displaystyle D(v_{1},v_{2})={\Big (}(v_{2}-v_{1})\;\mathbf {r} +\Delta u({\dot {\mathbf {c} }}+v_{2}\;{\dot {\mathbf {r} }}){\Big )}^{2}\ .}
Parameter des Zentralpunktes

Der Abstand wird minimal, wenn die Funktion {\displaystyle D(v_{1},v_{2})} minimal wird. Und dies ist der Fall, wenn die 1. partiellen Ableitungen Null sind:

{\displaystyle D_{v_{1}}=-2{\Big (}(v_{2}-v_{1})\;\mathbf {r} +\Delta u({\dot {\mathbf {c} }}+v_{2}\;{\dot {\mathbf {r} }}){\Big )}\cdot \mathbf {r} }
{\displaystyle \ =-2{\color {magenta}(v_{2}-v_{1}+\Delta u\;{\dot {\mathbf {c} }}\cdot \mathbf {r} )}=0\ ,}
{\displaystyle D_{v_{2}}=2{\Big (}(v_{2}-v_{1})\;\mathbf {r} +\Delta u({\dot {\mathbf {c} }}+v_{2}\;{\dot {\mathbf {r} }}){\Big )}\cdot (\mathbf {r} +\Delta u\;{\dot {\mathbf {r} }})}
{\displaystyle \ =2{\Big (}{\color {magenta}v_{2}-v_{1}+\Delta u\;{\dot {\mathbf {c} }}\cdot \mathbf {r} }+{\Delta u}^{2}({\dot {\mathbf {c} }}\cdot {\dot {\mathbf {r} }}+v_{2}{\dot {\mathbf {r} }}^{2}){\Big )}=0\ .}

Aus diesem Gleichungssystem für {\displaystyle v_{1},v_{2}} folgt für {\displaystyle \Delta u\to 0\ }:

Parameterdarstellung

Die Parameterdarstellung der Striktionslinie ist also

Doppelte Regelflächen

Sowohl auf dem einschaligen Hyperboloid als auch auf dem hyperbolischen Paraboloid liegen zwei Scharen von Geraden. Zu jeder Schar gehört eine Striktionslinie. Beim einschaligen Rotations-Hyperbolod fallen die zwei Striktionslinien zusammen.

Beispiele

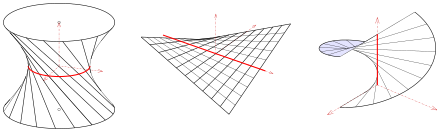
1) Einschaliges Rotations-Hyperboloid
{\displaystyle \mathbf {x} (u,v)={\begin{pmatrix}\cos u\\\sin u\\0\end{pmatrix}}+v\cdot {\begin{pmatrix}-\sin u\\\cos u\\k\end{pmatrix}}\ ,\ }

Die Zentralpunkte haben alle den Parameter v=0, d.h. die Striktionslinie ist der Einheitskreis in der x-y-Ebene.

Striktionslinien (rot) von einschaligem Rotations-Hyperboloid, hyperbolischem Paraboloid und Wendelfläche
2) Gerades Konoid

Bei einem geraden Konoid ist die Achse das gemeinsame Lot aller Erzeugenden. (Es gilt allgemein: Ein Punktepaar zweier windschiefer Geraden hat den kürzesten Abstand, wenn seine Verbindung das gemeinsame Lot der Geraden ist.) Also gilt für gerade Konoide

Die Achse eines geraden Konoids ist auch seine Striktionslinie.

Beispiele von geraden Konoiden sind das hyperbolische Paraboloid {\displaystyle z=xy} und die Wendelfläche.

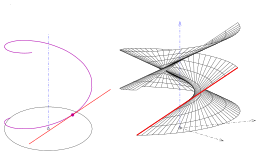
Schraubtorse, lila: Leitkurve und Striktionslinie
3) Torse

Jede vom allgemeinen Zylinder und Kegel verschiedene abwickelbare Regelfläche (Torse) ist eine Tangentenfläche, d.h. die Gesamtheit der Erzeugenden der Regelfläche besteht aus der Schar der Tangenten einer vorgegebenen Kurve \gamma. (Im Bild ist die Kurve eine Schraublinie. Dadurch entsteht eine Schraubtorse.) Allgemein gilt

Die Striktionslinie einer durch eine Kurve \gamma erzeugte Tangentenfläche ist die Kurve \gamma selbst.
4) Möbiusband
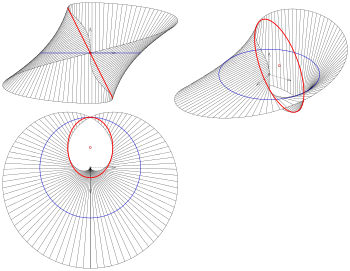
Striktionslinie (rot) eines Moebiusbandes

Für die oben angegebene Beschreibung eines Möbiusbandes ist

{\displaystyle \mathbf {c} (u)=(\cos 2u,\sin 2u,0)^{T}\ } ,
{\displaystyle \mathbf {r} (u)=(\cos u\cos 2u,\cos u\sin 2u,\sin u)^{T}\ .}

(Zum Bild: Damit die Striktionslinie völlig auf der dargestellten Fläche liegt, wurde das Band verbreitert.) Der Richtungsvektor \mathbf {r} ist in diesem Fall schon ein Einheitsvektor, was die Rechnung wesentlich vereinfacht.

Für den Parameter des jeweiligen Zentralpunktes ergibt sich {\displaystyle v={\frac {4\cos u}{1+4\cos ^{2}u}}} und schließlich die Parameterdarstellung der Striktionslinie

{\displaystyle \mathbf {x} (u)={\frac {1}{1+4\cos ^{2}u}}\;{\big (}\cos(2u),\sin(2u),-2\sin(2u){\big )}\ .}

Man erkennt leicht, dass diese Kurve in der Ebene {\displaystyle 2y+z=0} liegt. Um zu zeigen, dass diese ebene Kurve sogar

eine Ellipse mit Mittelpunkt {\displaystyle (-{\tfrac {2}{5}},0,0)} und den Halbachsen {\displaystyle a=1,b={\tfrac {3}{5}}} ist,

zeigt man, dass die x- und y-Koordinaten die Gleichung {\displaystyle \ {\tfrac {(x+{\tfrac {2}{5}})^{2}}{({\tfrac {3}{5}})^{2}}}+{\tfrac {y^{2}}{\tfrac {1}{5}}}=1\ } erfüllen. Also ist der Grundriss der Striktionslinie eine Ellipse und damit die Striktionslinie als Parallelprojektion auch.

Die Striktionslinie lässt sich einfacher durch die Parameterdarstellung

{\displaystyle \mathbf {x} (t)=\mathbf {f} _{0}+\mathbf {f} _{1}\cos t+\mathbf {f} _{2}\sin t\ } mit
{\displaystyle \mathbf {f} _{0}=(-{\tfrac {2}{5}},0,0)^{T},\ \mathbf {f} _{1}=({\tfrac {3}{5}},0,0)^{T},\ \mathbf {f} _{2}=(0,-{\tfrac {1}{\sqrt {5}}},{\tfrac {2}{\sqrt {5}}})^{T}}

beschreiben (s. Ellipse).

Zusammensetzung von Regelflächen

Man kann je zwei abwickelbare Regelflächen längs einer Geraden g bzw. h abschneiden und sie so zusammensetzen, dass aus g und h eine gemeinsame Gerade der zusammengesetzten Fläche mit einer neuen gemeinsamen Tangentialebene von dieser wird.

Bei einer nicht abwickelbaren und einer abwickelbaren Regelfläche ist die so zusammengesetzte Fläche längs der gemeinsamen Erzeugenden nicht differenzierbar. Die gemeinsame Erzeugende ist als Kante sichtbar, wobei die Kante an verschiedenen Punkten der Erzeugenden verschieden deutlich hervortritt. Bei zwei nicht abwickelbaren Regelflächen kann die so zusammengesetzte Fläche längs der gemeinsamen Erzeugenden differenzierbar sein, ist es im Allgemeinen aber nicht.

Außermathematische Anwendung

Regelflächen können nicht nur in der Mathematik, sondern auch außerhalb davon in Konstruktionen und Ingenieursarbeit verwendet werden. Ein gutes Beispiel hierfür ist die Arbeit des Architekten/Mathematikers Antoni Gaudí. Das Gewölbe der La Sagrada Família beschreibt hierbei mehrere Hyperboloide, hyperbolische Paraboloide und Helikoide.

Literatur

Trenner
Basierend auf einem Artikel in: Wikipedia.de
Seitenende
Seite zurück
©  biancahoegel.de
Datum der letzten Änderung: Jena, den: 10.04. 2023