Fläche (Mathematik)

Sphäre

Eine Fläche im anschaulichen Sinn ist eine zweidimensionale Teilmenge des dreidimensionalen Raumes, beispielsweise eine Ebene, eine zweidimensionale geometrische Figur oder die Begrenzungsfläche eines dreidimensionalen Körpers. Eine Fläche kann somit sowohl flach als auch gekrümmt sein.

Ein Maß für die Größe einer Fläche ist der Flächeninhalt. Umgangssprachlich wird der Flächeninhalt oftmals ebenfalls als „Fläche“ bezeichnet. Dieser Artikel behandelt das mathematische Objekt „Fläche“, nicht den Flächeninhalt.

Je nach Teilgebiet der Mathematik unterscheiden sich die genauen Definitionen einer Fläche. Gemeinsam haben alle Definitionen, dass die Fläche ein zweidimensionales Objekt ist.

Elementargeometrie

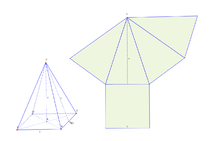
Oberfläche einer quadratischen Pyramide, abgewickelt als Körpernetz

Die Elementargeometrie betrachtet, in der Ebene, beispielsweise Vielecke oder das Innere eines Kreises, und nennt solche Objekte Flächen. Im dreidimensionalen Raum betrachtet die Elementargeometrie Objekte wie den Zylinder und den Kegel. Diese geometrischen Körper werden durch Flächen (auch Seitenflächen genannt) begrenzt. Zusammen bilden sie die Oberfläche des Körpers. In eine Ebene aufgefaltet bzw. abgewickelt ergeben sie das Netz des Körpers. In der Elementargeometrie wird der Begriff der Fläche erklärt, jedoch nicht in mathematischer Strenge definiert.

Flächen im Raum

Durch Gleichungen beschriebene Flächen

Einschaliges Hyperboloid

→ Hauptartikel: Implizite Fläche

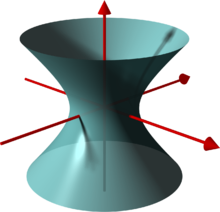
Viele Flächen lassen sich durch Gleichungen beschreiben: Die Sphäre (Kugelfläche) mit Mittelpunkt (0,0,0) und Radius durch $x^{2}+y^{2}+z^{2}=r^{2}$ oder das einschalige Hyperboloid durch $x^{2}+y^{2}-z^{2}=1$ . Man kann jede solche Gleichung auf die Form f(x,y,z)=0 mit einer Funktion bringen. Nicht jede solche Gleichung beschreibt eine Fläche, z.B. besteht die Lösungsmenge von $x^{2}+y^{2}+z^{2}=0$ aus dem einzelnen Punkt (0,0,0) .

Sei $f\colon \mathbb {R} ^{3}\to \mathbb {R}$ eine glatte Funktion mit der Eigenschaft, dass für jede Lösung $(x_{0},y_{0},z_{0})$ der Gleichung f(x,y,z)=0 der Gradient

${\text{grad }}f=\left({\frac {\partial f}{\partial x}},{\frac {\partial f}{\partial y}},{\frac {\partial f}{\partial z}}\right)$

nicht null ist. Dann nennt man $0$ einen regulären Wert von , und die Menge $\{(x,y,z)\in \mathbb{R} ^{3}:f(x,y,z)=0\}$ eine reguläre Fläche. In der allgemeinen Definition einer regulären Fläche müssen zu jedem Punkt $(x_{0},y_{0},z_{0})\in S$ eine Umgebung $V\subseteq \mathbb{R} ^{3}$ und eine differenzierbare Funktion $f\colon V\to \mathbb {R}$ existieren, so dass $0$ ein regulärer Wert von ist und $S\cap V=\{(x,y,z)\in V:f(x,y,z)=0\}$ gilt.

Whitney-Regenschirm

Eine Fläche heißt reelle algebraische Fläche, wenn sie sich durch eine Polynomfunktion $f\in \mathbb{R} [x,y,z]$ beschreiben lässt. Der genaue Flächenbegriff der reellen algebraischen Geometrie entspricht nicht immer der elementaren Vorstellung: Ein Beispiel ist der Whitney-Regenschirm $x^{2}-y^{2}z=0$ , der neben der im Bild sichtbaren Fläche noch die -Achse als Stiel beinhaltet, aber diese beiden Teile lassen sich algebraisch nicht voneinander trennen.

Zylinder

Doppelkegel

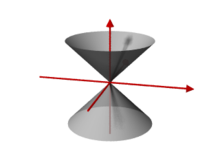
Flächen zweiter Ordnung sind algebraische Flächen, die durch ein Polynom vom Grad 2 gegeben sind. Beispiele sind der Zylinder, der auch in der Elementargeometrie untersucht wird und als mögliche Gleichung x^2+y^2=1 hat, oder der Doppelkegel mit Gleichung $x^{2}+y^{2}-z^{2}=0$ . Der Doppelkegel ist keine reguläre Fläche, er hat im Nullpunkt eine Singularität.

Durch Parametrisierungen beschriebene Flächen

Eine Parametrisierung eines Flächenstücks ist eine auf einem Teil $U\subseteq \mathbb{R} ^{2}$ der Ebene definierte, glatte Immersion $\phi \colon U\to \mathbb {R} ^{3}$ . (Eine Abbildung heißt Immersion, wenn die Jacobi-Matrix von $\phi$ in jedem Punkt von vollen Rang hat, bzw. die Ableitung als von ihr dargestellte lineare Abbildung injektiv ist.) Im einfachsten Fall kann $\phi$ der Graph $(u,v)\mapsto (u,v,f(u,v))$ einer Funktion $f\colon \mathbb {R} ^{2}\to \mathbb {R}$ sein. Erlaubt man noch einen Rollenwechsel bei x,y,z , dann genügen Funktionsgraphen zur lokalen Beschreibung beliebiger Flächenstücke.

Eine reguläre Fläche ist in diesem Kontext eine Teilmenge $S\subset \mathbb{R} ^{3}$ , so dass zu jedem Punkt $s\in S$ eine Umgebung $V\subseteq \mathbb{R} ^{3}$ und eine Parametrisierung $\phi \colon U\to V$ existiert, so dass $\phi$ einen Homöomorphismus $U\to S\cap V$ induziert. Diese Beschreibung ist zu der weiter oben gegebenen äquivalent.

Unter einer immersierten Fläche versteht man allerdings nicht die offensichtliche Abschwächung der vorstehenden Definition, sondern eine abstrakte Fläche (s.u.) zusammen mit einer Immersion $S\to \mathbb{R} ^{3}$ .

Eine Regelfläche ist eine Fläche, die für ein Intervall $I\subseteq \mathbb{R}$ eine Parametrisierung der Form

$\phi \colon I\times \mathbb {R} \to \mathbb {R} ^{3},\ \ (u,v)\mapsto p(u)+vr(u)$

mit Funktionen $p,r\colon \mathbb {R} \to \mathbb {R} ^{3}$ besitzt. An jeden Stützpunkt p(u) ist also eine -Gerade mit Richtung r(u) angeheftet. (Der Begriff „Regelfläche“ entstand aus einer Falschübersetzung des englischen Begriffs „ruled surface“: So bedeutet „rule“ nicht nur „Regel“, sondern auch „linieren“.) Falls $r(u)\neq 0$ für alle und p'(u) nicht im Erzeugnis von r(u) und r'(u) liegt, handelt es sich um eine immersierte Fläche. Der Flächenanteil des Whitney-Regenschirms ist eine mit Ausnahme der Spitze immersierte Regelfläche, das einschalige Hyperboloid eine reguläre Regelfläche.

Eine Rotationsfläche ist eine Fläche, die durch die Rotationsbewegung eines Funktionsgraphen um eine Koordinatenachse erzeugt wird. Ist $f\colon \mathbb {R} \to \mathbb {R}$ eine glatte Funktion, dann erhält man durch Rotation von $\{(x,y,z)\in \mathbb{R} ^{3}:y=f(x),z=0\}$ um die -Achse die Fläche

$(u,v)\mapsto (u,f(u)\cos v,f(u)\sin v)$

Wenn f(u)>0 für alle , erhält man eine reguläre Fläche. Hat Nullstellen, handelt es sich nicht um eine immersierte Fläche.

Differentialgeometrie regulärer Flächen

Tangentialebene und Normalenvektor

Sei eine reguläre Fläche und ein Punkt auf . Ist lokal bei durch eine reguläre Parametrisierung $\phi \colon U\to \mathbb {R} ^{3}$ mit $x_{0}\in U\subseteq \mathbb{R} ^{2}$ und $\phi (x_{0})=x$ gegeben, dann ist das Bild der Ableitung $d\phi (x_{0})\colon \mathbb {R} ^{2}\to \mathbb {R} ^{3}$ ein zweidimensionaler Unterraum $T_{x}S$ , den man die Tangentialebene von in nennt. Die anschauliche Tangentialebene erhält man, indem man den Unterraum um den Vektor verschiebt. Ein Normalenvektor ist ein Vektor, der orthogonal zur Tangentialebene ist.

In der Beschreibung durch lokale Gleichungen sei $V\subseteq \mathbb{R} ^{3}$ eine offene Teilmenge und $f\colon V\to \mathbb {R}$ eine Funktion mit regulärem Wert $0$ , so dass $V\cap S=\{x\in V:f(x)=0\}$ gilt. Dann ist der Gradient von in allen Punkten von $V\cap S$ jeweils ein Normalenvektor, und man kann die Tangentialebene als diejenige Ebene verstehen, die senkrecht auf dem Gradienten steht.

Krümmung

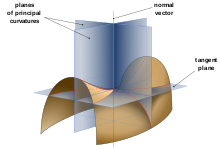
Fläche mit Normalenvektor und Hauptkrümmungsebenen

Sei eine reguläre Fläche, ein Punkt auf und $n_{x}$ ein Normalenvektor der Länge im Punkt . Für einen variablen Tangentialvektor der Länge im Punkt spannen $n_{x}$ und eine (orientierte) Ebene $E_{{x,v}}$ auf, und der Schnitt $S\cap E_{{x,v}}$ ist lokal eine reguläre Kurve. Sei $\kappa _{x}(v)$ die Krümmung dieser Kurve, d.h., wenn die nach Bogenlänge parametrisierte Kurve mit c(0)=x ist, dann ist $c''(0)=-\kappa _{x}(v)\cdot n_{x}$ . Die Zahl $\kappa _{x}(v)$ heißt Krümmung von in Richtung . Hat $\kappa _{x}(v)$ nicht für alle denselben Wert, dann gibt es zwei zueinander orthogonale Richtungen, in denen $\kappa _{x}$ das Maximum $\kappa_1$ bzw. das Minimum $\kappa_2$ annimmt. $\kappa_1$ und $\kappa_2$ heißen die Hauptkrümmungen von im Punkt , die zugehörigen Richtungen Hauptkrümmungsrichtungen. Aus ihnen definiert man die gaußsche Krümmung $K=\kappa _{1}\cdot \kappa _{2}$ und die mittlere Krümmung $H={\tfrac {\kappa _{1}+\kappa _{2}}2}$ . Wechselt man die Richtung des Normalenvektors, ändern die Hauptkrümmungen ihr Vorzeichen, so dass die gaußsche Krümmung gleich bleibt und die mittlere Krümmung ebenfalls das Vorzeichen wechselt. Die Sphäre mit Radius hat Gaußkrümmung $1/R^{2}$ und mittlere Krümmung 1/R (für nach außen zeigende Normalenvektoren).

Setzt man $\kappa _{x}$ durch die Festlegung $\kappa _{x}(\lambda v)=\lambda ^{2}\cdot \kappa _{x}(v)$ für alle $\lambda\in\R$ zu einer auf der ganzen Tangentialebene definierten Funktion $T_{x}S\to \mathbb{R}$ fort, erhält man eine quadratische Form. Die zugehörige Bilinearform heißt zweite Fundamentalform ${\text{II}}_{x}$ und lässt sich auch als ${\text{II}}_{x}(v_{1},v_{2})=\langle v_{1},L_{x}v_{2}\rangle$ mit der Weingartenabbildung $L_{x}:T_{x}S\to T_{x}S$ schreiben, die wiederum die Ableitung des Normalenvektors, aufgefasst als Gauß-Abbildung $S\to S^{2}$ , ist. Die Hauptkrümmungen und Hauptkrümmungsrichtungen sind die Eigenwerte und Eigenvektoren der Weingartenabbildung, der Zusammenhang zur ersten Beschreibung wird durch den Trägheitssatz von Sylvester hergestellt.

Abwickelbare Flächen sind eine Klasse von Flächen, deren gaußsche Krümmung überall den Wert 0 hat. Wenn eine Fläche gaußsche Krümmung 0 hat und keine planaren Punkte besitzt, d.h. keine Punkte, in denen beide Hauptkrümmungen 0 sind, dann ist sie abwickelbar. Flächen mit gaußscher Krümmung 0 sind lokal isometrisch zur Ebene, d.h., sie lassen sich ohne innere Formverzerrung auf die Ebene abbilden. Beispiele sind Zylinder und Kegel, bei denen die Abbildung in die Ebene durch das Abwickeln des Mantels gegeben ist.

Krümmungslinie

Eine reguläre Kurve auf der Fläche heißt Krümmungslinie, falls ihre Tangentenrichtung in jedem Punkt eine Hauptkrümmungsrichtung ist. Eine wichtige Hilfe bei der Bestimmung von Krümmungslinien bietet der Satz von Dupin.

Beispiele:

Die auf einem senkrechten Kreiszylinder liegenden Kreise und Geraden.
Die auf einem einschaligen Rotationshyperboloid liegenden Kreise und dazu senkrechten Hyperbeln.
Kreise auf einer Dupinschen Zyklide.

Asymptotenlinie

Eine reguläre Kurve auf einer Fläche mit negativer gaußscher Krümmung (die Indikatrix ist eine Hyperbel) heißt Asymptotenlinie, falls ihre Tangentenrichtung in jedem Punkt die Richtung einer Asymptote der Indikatrix des Punktes hat. Es gibt also in jedem Punkt zwei Asymptotenlinien. Der Winkel zwischen beiden wird von den Krümmungslinien halbiert. Z.B. sind die Geraden auf einem einschaligen Hyperboloid Asymptotenlinien.

Flächeninhalt und Minimalflächen

Die Minimalfläche von Scherk, $e^{z}\cdot \cos x=\cos y$

Mit Hilfe der gramschen Determinante kann man den Flächeninhalt eines Flächenstücks definieren und allgemeiner eine Integrationstheorie für Flächen entwickeln: Ist $\phi \colon U\to \mathbb {R} ^{3}$ ein Flächenstück der Fläche und $f\colon S\to \mathbb {R}$ eine Funktion, dann ist das Integral von definiert als

$\int _{{\phi (U)}}f=\int _{U}{\sqrt {\det(d\phi (u)\cdot d\phi (u)^{T})}}\cdot f(\phi (u))\,du$

Für Integrale über ganz muss man die Fläche evtl. unterteilen.

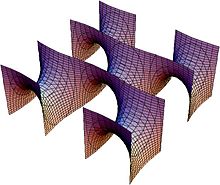
Eine Minimalfläche ist eine Fläche, die lokal minimalen Flächeninhalt hat, genauer deren Parametrisierung ein kritischer Punkt für das Flächeninhaltsfunktional ist. Derartige Formen nehmen beispielsweise Seifenhäute an, wenn sie über einen entsprechenden Rahmen (wie etwa einem Blasring) gespannt sind. Minimalflächen sind auch dadurch charakterisiert, dass ihre mittlere Krümmung überall den Wert 0 hat.

Die gaußsche Krümmung ist ein Maß für die Abweichung des lokalen Flächeninhalts von den Werten der Ebene: Bezeichnet A(r) den Flächeninhalt der Scheibe mit Radius um einen Punkt, dann ist die gaußsche Krümmung in diesem Punkt:

$K={\frac {12}{\pi }}\cdot \lim _{{r\to 0}}{\frac {\pi r^{2}-A(r)}{r^{4}}}$

Orientierbarkeit

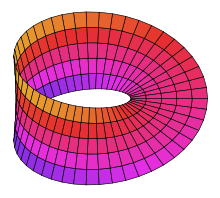
→ Hauptartikel: Orientierung (Mathematik) und Orientierte Fläche

Möbiusband

Der Begriff der Orientierbarkeit fasst die Situation, dass bei einer Fläche global zwei Seiten unterschieden werden können. Das Paradebeispiel für eine Fläche, bei der das nicht möglich ist, die also nicht orientierbar ist, ist das Möbiusband. Für eine reguläre Fläche kann man die zwei Seiten dadurch beschreiben, dass es in jedem Punkt zwei Normalenvektoren (d.h. senkrecht auf der Fläche stehend) der Länge 1 gibt, zu jeder Seite hin einen. Kann man nun einheitlich (d.h. glatt) für jeden Punkt eine der beiden Richtungen auswählen, nennt man die Fläche orientierbar. (Es gibt andere Charakterisierungen von Orientierbarkeit, die keinen Gebrauch vom umgebenden Raum oder der Differenzierbarkeit machen, s.u.) Ist die Nullstellenmenge der Funktion $f\colon \mathbb {R} ^{3}\to \mathbb {R}$ mit regulärem Wert $0$ , dann ist

${\frac {{\text{grad }}f}{|{\text{grad }}f|}}$

in jedem Punkt von ein Normalenvektor der Länge 1, also ist eine solche Fläche orientierbar. Ebenso ist jede kompakte reguläre Fläche ohne Rand orientierbar (nicht jedoch jede kompakte abstrakte Fläche, wie z.B. die projektive Ebene oder die kleinsche Flasche).

Flächen im Bereich der Topologie

Ein Rotationsellipsoid

Die nicht orientierbare Kleinsche Flasche

In mathematischen Teilgebieten wie der Topologie, der Differentialtopologie, der riemannschen Geometrie oder der Funktionentheorie betrachtet man Flächen nicht mehr als Objekte, die in den dreidimensionalen Raum eingebettet sind, vielmehr verzichtet man auf den umgebenden Raum und betrachtet nur die Fläche für sich. Man spricht von abstrakten Flächen oder von 2-Mannigfaltigkeiten.

Motivation

Sei $U\subseteq \mathbb{R} ^{2}$ eine offene Teilmenge und $\phi \colon U\to \mathbb {R} ^{3}$ eine reguläre Parametrisierung eines Flächenstücks $S=\phi (U)$ . Man kann sich nun fragen, welche Daten man auf vorgeben muss, um Aussagen über zu treffen. Nach Definition ist für $u\in U$ die Ableitung $d\phi (u)$ ein Isomorphismus $\mathbb{R} ^{2}\to T_{{\phi (u)}}S$ . Die Länge von Tangentialvektoren kann man also in eine Bilinearform

$g_{u}\colon \mathbb{R} ^{2}\times \mathbb{R} ^{2}\to \mathbb{R} ,\ \ (v_{1},v_{2})\mapsto \langle d\phi (u)v_{1},d\phi (u)v_{2}\rangle$

übersetzen, die hier erste Fundamentalform, im allgemeinen Kontext aber riemannsche Metrik genannt wird. Die gramsche Determinante für $\phi$ ist gleich der Determinante der Darstellungsmatrix von , also enthält die riemannsche Metrik bereits die Information über Flächeninhalte und Integrale auf . Die zweite Fundamentalform und damit die Hauptkrümmungen kann man jedoch nicht alleine an ablesen, wie das folgende Beispiel eines Zylinderstücks zeigt:

$\phi \colon U=(-\pi ,\pi )\times \mathbb{R} \to \mathbb{R} ^{3},\ \ (u_{1},u_{2})\mapsto (\cos u_{1},\sin u_{1},u_{2})$

Für jedes $u\in U$ ist $g_{u}$ das Standardskalarprodukt, also kann die riemannsche Metrik nicht zwischen einem Zylinder und einer Ebene unterscheiden. Aber: Das Theorema egregium von Carl Friedrich Gauß besagt, dass die gaußsche Krümmung nur von der riemannschen Metrik abhängt.

Damit lässt sich der gaußsche Krümmungsbegriff auf Flächen übertragen, für die keine Einbettung in den euklidischen Raum bekannt ist oder auch nur existiert. Ein Beispiel ist die hyperbolische Ebene, die über eine naheliegende riemannsche Metrik verfügt, mit der sie konstante negative Krümmung hat, aber nach einem Satz von David Hilbert keine isometrische Einbettung in den euklidischen Raum besitzt. (Isometrisch bedeutet hier, dass die Einbettung die vorgegebene Metrik induziert.)

Ein anderes Phänomen sind Flächen wie die reelle projektive Ebene, die überhaupt keine Einbettung in den euklidischen Raum erlauben, sondern lediglich Immersionen (z.B. als Boysche Fläche). Man kann sie zwar in höherdimensionale Räume einbetten, aber da man letztlich in Eigenschaften interessiert ist, die unabhängig von der Einbettung sind, ist es vorteilhaft, eine Sprache zu entwickeln, in der keine Einbettungen mehr vorkommen.

Definition

Im Bereich der Topologie wird der Begriff Fläche als Synonym für 2-dimensionale Mannigfaltigkeit verwendet. Das heißt, eine Fläche ist ein besonderer topologischer Raum, eine zweidimensionale topologische Mannigfaltigkeit. Das ist per Definition ein Hausdorff-Raum, der lokal homöomorph zu $\mathbb {R} ^{2}$ ist. Die lokalen Homöomorphismen werden Karten genannt, ihre Gesamtheit bildet einen Atlas. Da die Fläche lokal homöomorph zum zweidimensionalen Raum $\mathbb {R} ^{2}$ ist, definiert man, dass die Dimension der Fläche gerade zwei ist. Beispielsweise ist eine Kugeloberfläche eine Fläche in Sinne der Topologie.

Eine kompakte Fläche wird auch geschlossen genannt, wenn betont werden soll, dass es sich um eine Fläche ohne Rand handelt. Flächen mit Rand als spezielle Mannigfaltigkeiten mit Rand werden im Abschnitt Verallgemeinerungen definiert.

Beispiele

Torus

Die einfachsten kompakten Flächen sind

die 2-dimensionale Sphäre
der 2-dimensionale Torus.

Zusammenhängende Summe

Weitere kompakte, orientierbare Flächen erhält man als zusammenhängende Summe von g Tori. (Die zusammenhängende Summe zweier Flächen wird gebildet, indem man aus beiden Flächen jeweils einen 2-Ball herausschneidet und die beiden 1-dimensionalen Randsphären verklebt.) Die Zahl g heißt das Geschlecht der Fläche.

Eine explizite Beschreibung der Fläche vom Geschlecht g (als glatte algebraische Varietät und insbesondere 2-dimensionale Mannigfaltigkeit) ist zum Beispiel

$S_{g}=\left\{(w,z)\in \mathbb {C} ^{2}:w^{2}=(z-g)\ldots (z-1)z(z+1)\ldots (z+g)\right\}$ .

Die Euler-Charakteristik der Fläche vom Geschlecht g ist 2 − 2g.

Die Sphäre trägt eine sphärische Metrik, der Torus flache Metriken, die Flächen vom Geschlecht mindestens 2 tragen hyperbolische Metriken. Der Modulraum hyperbolischer Metriken auf einer gegebenen Fläche heißt Teichmüller-Raum der Fläche.

Flächen mit zusätzlichen Strukturen

Die zuvor angeführten Flächen in der Topologie sind das Grundgerüst für die spezielleren Flächen, die in der Differentialtopologie, der riemannschen Geometrie oder der Funktionentheorie untersucht werden. In diesen mathematischen Teilgebieten wird die Fläche noch mit einer zusätzlichen Struktur ausgestattet.

Im Bereich der Differentialtopologie stattet man die topologische Fläche noch zusätzlich mit einer differenzierbaren Struktur aus, um Funktionen, die auf der Fläche definiert sind, differenzieren und um die Tangentialebene definieren zu können. Da die Fläche ja ohne umgebenden Raum definiert wurde, kann im Gegensatz zum vorigen Abschnitt die Orientierbarkeit der Fläche nicht mit Hilfe eines Normalenvektors definiert werden. Aus diesem Grund wird eine (äquivalente) Definition mittels Karten und Tangentialebene gewählt. Die Eigenschaft der Orientierbarkeit einer Fläche hängt also nicht vom umgebenden Raum ab.

In der Funktionentheorie ergänzt man die Fläche nicht um eine differenzierbare Struktur, sondern um eine komplexe Struktur. Solche Flächen werden riemannsche Flächen genannt, und die komplexe Struktur ermöglicht es auf ihnen den Begriff der holomorphen Funktion zu definieren. Im Bereich der riemannschen Flächen gibt zwei unterschiedliche Dimensionsbegriffe. Zum einen ist sie wieder ein Spezialfall der topologischen Fläche und hat damit die Dimension zwei, zum anderen betrachtet man in der Funktionentheorie meistens die komplexe Zahlenebene $\mathbb {C} \cong \mathbb {R} ^{2}$ und versteht die riemannschen Flächen als eine Verallgemeinerung dieser. In diesem Kontext hat die riemannsche Fläche die (komplexe) Dimension eins und wird daher auch als „komplexe Kurve“ interpretiert. Kompakte riemannsche Flächen sind projektive algebraische Kurven, das heißt, sie lassen sich in einen komplexen projektiven Raum einbetten, so dass das Bild durch Polynomgleichungen beschrieben wird.

Auf einer differenzierbaren Fläche kann auch eine riemannsche Metrik gegeben sein, das ist ein Skalarprodukt auf jeder Tangentialebene, das differenzierbar vom Basispunkt abhängt. Jede reguläre Fläche im $\mathbb {R} ^{3}$ erhält über die Einschränkung des Standardskalarprodukts eine riemannsche Metrik. Eine riemannsche Metrik induziert auf orientierbaren Flächen eine konforme Struktur, in der die Längenmessung verlorengeht, aber die Information über Winkel erhalten bleibt. Die 90°-Drehung auf den Tangentialräumen ist eine fastkomplexe Struktur, und im Fall von Flächen ist jede fastkomplexe Struktur eine komplexe Struktur, das heißt jede Fläche mit einer riemannschen Metrik ist auf kanonische Weise eine riemannsche Fläche.

Klassifikation

Orientierbare geschlossene Fläche vom Geschlecht 3

Der Klassifikationssatz gibt eine Liste von Flächen an, so dass jede geschlossene Fläche zu genau einer von ihnen homöomorph ist.

Eine orientierbare Fläche ist homöomorph zur verbundenen Summe von $g\ge0$ Tori. Für handelt es sich um die Sphäre, für um den Torus. Die Zahl ist das Geschlecht der Fläche.
Eine nicht orientierbare Fläche ist homöomorph zu einer verbundenen Summe von projektiven Ebenen.

Für geschlossene differenzierbare Flächen ergibt sich dieselbe Klassifikation: jede Fläche ist diffeomorph zu genau einer der Flächen aus der Liste. Allgemein stimmen für geschlossene Flächen die Klassifikationen nach Homotopieäquivalenz, Homöomorphie, PL-Äquivalenz und Diffeomorphie alle überein.

Für riemannsche Flächen überträgt sich die Klassifikation nicht: Jede riemannsche Fläche ist orientierbar und eine orientierbare geschlossene Fläche kann wesentlich verschiedene komplexe Strukturen tragen.

Für Geschlecht 0 gibt es nur eine riemannsche Fläche, die projektive Gerade oder riemannsche Zahlenkugel.
Für Geschlecht 1 sind die riemannschen Flächen (bis auf die Wahl eines Basispunkts) elliptische Kurven und durch ihre j-Invariante klassifiziert.
Für Geschlecht werden die riemannschen Flächen durch den Teichmüller-Raum parametrisiert, der selbst eine -dimensionale komplexe Mannigfaltigkeit ist.

Der Uniformisierungssatz besagt, dass es für die (nicht notwendigerweise kompakte) universelle Überlagerung einer riemannschen Fläche nur drei Möglichkeiten gibt (entsprechend der Unterscheidung g=0,g=1,g>1 ):

die riemannsche Zahlenkugel
die komplexe Zahlenebene
die obere Halbebene

Geschlossene Flächen mit riemannscher Metrik sind für eine Klassifikation zu kompliziert. Einfach zusammenhängende Flächen mit konstanter Krümmung, die nicht notwendigerweise kompakt, aber vollständig sind, sind jedoch klassifizierbar: Durch Skalierung kann man sich auf die Krümmungen +1,0,-1 beschränken. Dann gibt jeweils bis auf Isometrie jeweils nur eine derartige Fläche:

: die Einheitssphäre
$0$ : die euklidische Ebene
: die hyperbolische Ebene

Diese Aussage gilt analog für beliebige Dimensionen. Nach einem Satz von Jacques Hadamard ist auch jede einfach zusammenhängende vollständige Fläche nicht notwendigerweise konstanter, aber überall nichtpositiver Krümmung diffeomorph zur Ebene.

Verallgemeinerungen

Nimmt man in der Definition topologischer oder differenzierbarer Flächen noch die Halbebene $\{(x,y)\in \mathbb{R} ^{2}:x\geq 0\}$ als Modell hinzu, erhält man den Begriff der Fläche mit Rand. Punkte der Fläche, die auf die Gerade $\{(x,y)\in \mathbb{R} ^{2}:x=0\}$ abgebildet werden, werden Randpunkt genannt. Die abgeschlossene Einheitskreisscheibe in der Ebene ist beispielsweise eine differenzierbare Fläche mit Rand, das abgeschlossene Einheitsquadrat ist eine topologische Fläche mit Rand.
Teilmengen von $\mathbb {R} ^{n}$ , die ähnliche Differenzierbarkeitseigenschaften wie reguläre Flächen haben, nennt man Untermannigfaltigkeiten. Untermannigfaltigkeiten der Dimension nennt man Hyperflächen.
Höherdimensionale Analoga der abstrakten Flächen sind topologische Mannigfaltigkeiten und differenzierbare Mannigfaltigkeiten.
Höherdimensionale Analoga der riemannschen Flächen sind komplexe Mannigfaltigkeiten. Komplexe Mannigfaltigkeiten der Dimension 2 nennt man komplexe Flächen. Sie sind vierdimensionale reelle Mannigfaltigkeiten.

Basierend auf einem Artikel in:

Wikipedia.de