
Gauß-Abbildung
In der Differentialgeometrie
bildet die Gauß-Abbildung (benannt nach Carl F. Gauß)
eine Fläche
im euklidischen
Raum
auf die Einheitssphäre
ab.
Gauß schrieb erstmals im Jahr 1825 über das Thema und veröffentlichte es 1827.
Definition
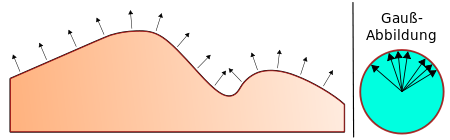
Auf einer gegebenen orientierten
Fläche ,
ist die Gauß-Abbildung eine stetige Abbildung
,
so dass
ein zur Fläche
orthonormaler Einheitsvektor bei
,
nämlich der Normalenvektor
an
bei
,
ist.
Eigenschaften
Die Gauß-Abbildung kann global, also für alle ,
nur genau dann definiert werden, wenn die Fläche orientierbar ist. Lokal,
das heißt auf einem kleinen Stück der Oberfläche, kann sie immer definiert
werden. Die Funktionaldeterminante
der Gauß-Abbildung ist gleich der Gauß-Krümmung,
und das Differential
der Gauß-Abbildung wird Weingartenabbildung
oder auch Form-Operator genannt.
Verallgemeinerung
Analog zu obiger Definition kann die Gauß-Abbildung für n-dimensionale
orientierte Hyperflächen
im
definiert werden.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 01.09. 2020