
Gaußsche Krümmung
In der Theorie der Flächen
im dreidimensionalen
euklidischen
Raum (),
einem Gebiet der Differentialgeometrie,
ist die gaußsche Krümmung (das gaußsche Krümmungsmaß), benannt
nach dem Mathematiker Carl
Friedrich Gauß, der wichtigste Krümmungsbegriff
neben der mittleren
Krümmung.
Definition
Gegeben seien eine reguläre
Fläche im
und ein Punkt dieser Fläche. Die gaußsche Krümmung
der Fläche in diesem Punkt ist das Produkt
der beiden Hauptkrümmungen
und
.
Dabei sind
und
die beiden Hauptkrümmungsradien.
Beispiele
- Im Falle einer Kugel(oberfläche) mit Radius
ist die gaußsche Krümmung gegeben durch
.
- In einem beliebigen Punkt auf der gekrümmten Fläche eines geraden Kreiszylinders ist die gaußsche Krümmung gleich 0.
- In einem beliebigen Punkt auf der gekrümmten Fläche eines geraden Kreiskegels ist die gaußsche Krümmung gleich 0.
Berechnung
- Sind
,
,
bzw.
,
,
die Koeffizienten der ersten bzw. zweiten Fundamentalform, so gilt folgende Formel:
- Ist die betrachtete Fläche der Graph
einer Funktion
über dem Parameterbereich
, also
für alle
, so gilt für die gaußsche Krümmung:
-
- Hierbei bezeichnen
und
die ersten und
,
und
die zweiten partiellen Ableitungen von
.
- Ist die Fläche als Nullstellenmenge
einer Funktion
mit regulärem Wert
gegeben, dann berechnet sich die Gaußsche Krümmung aus der Formel
-
- Dabei ist
der Betrag des Gradienten und
die Adjunkte der Hesse-Matrix von
.
Eigenschaften
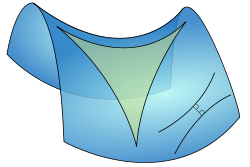
Vorzeichen
In elliptischen
Punkten ist die gaußsche Krümmung positiv (),
in hyperbolischen Punkten negativ (
)
und in parabolischen Punkten oder Flachpunkten verschwindet sie.
Eigenschaft der inneren Geometrie
Die gaußsche Krümmung hängt nur von der inneren Geometrie der gegebenen Fläche ab. Dieser Satz ist ein Korollar aus der Formel von Brioschi:
Dabei sind ,
und
die Koeffizienten der ersten Fundamentalform. Die Bezeichnungen
,
usw. stehen für erste und zweite partielle
Ableitungen nach den Parametern
und
,
mit denen die gegebene Fläche parametrisiert wird. Diese Gleichung ist unter
anderem eine der notwendigen Integrationsbedingungen der Gauß-Weingarten-Gleichungen.
Eine weitere Formel zur Berechnung der gaußschen Krümmung lautet:
Im Falle einer orthogonalen Parametrisierung ()
reduziert sich diese Formel auf
Wenn die Fläche isotherm parametrisiert ist, d.h., es gilt
und
,
dann schreibt sich
mit dem Laplaceoperator
.
Totalkrümmung
der Gaußschen Krümmung
über eine Teilmenge
einer Fläche bezeichnet man als deren Totalkrümmung. Bei Vielecken, deren
Kanten Geodätische
sind, besteht ein Zusammenhang zwischen der Totalkrümmung und der
Innenwinkelsumme. Beispielsweise gilt für die Innenwinkelsumme
eines geodätischen Dreiecks:
Die Totalkrümmung eines geodätischen Dreiecks entspricht also der Abweichung der Innenwinkelsumme von π: Die Innenwinkelsumme eines sich auf einer positiv gekrümmten Fläche befindenden Dreiecks überschreitet π, auf einer negativ gekrümmten Fläche liegt die Innenwinkelsumme unterhalb von π. Beträgt die Gaußkrümmung null, so beträgt die Innenwinkelsumme wie im ebenen Fall exakt π.
Eine Verallgemeinerung dieses Sachverhaltes ist der Satz von Gauß-Bonnet, der einen Zusammenhang zwischen der Gaußschen Krümmung einer Fläche und der geodätischen Krümmung der zugehörigen Randkurve beschreibt.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 29.12. 2020