Satz von Gauß-Bonnet

Der Satz von Gauß-Bonnet (nach Carl Friedrich Gauß und Pierre Ossian Bonnet) ist eine wichtige Aussage über Flächen, die ihre Geometrie mit ihrer Topologie verbindet, indem eine Beziehung zwischen Krümmung und Euler-Charakteristik hergestellt wird. Dieser Satz wurde von beiden Mathematikern unabhängig voneinander gefunden.

Während Gauß seine Arbeiten dazu nicht vollständig veröffentlichte (in den Disquisitiones circa superficies curvas von 1827 ist ein Spezialfall), wurde die Integralformel von Gauß und Bonnet zuerst 1848 von Bonnet veröffentlicht.

Flächen mit glatten Rand

Aussage

Sei eine kompakte und orientierbare zweidimensionale riemannsche Mannigfaltigkeit mit Rand $\partial M$ . Bezeichne mit die Gaußkrümmung in den Punkten von und mit k_g die geodätische Krümmung der Randkurve $\partial M$ . Dann gilt

$\int_M K\;dA+\int_{\partial M}k_g\;ds=2\pi\chi(M) ,$

wobei $\chi(M)$ die Euler-Charakteristik von ist. Der Satz kann im Besonderen auf Mannigfaltigkeiten ohne Rand angewendet werden. Dann fällt der Term $\textstyle \int_{\partial M}k_g\;ds$ weg.

Man kann den Satz von Gauß-Bonnet auch auf simpliziale Flächen verallgemeinern, wobei man den Winkeldefekt einer Ecke als diskrete Gaußkrümmung definiert.

Erklärung des Satzes

Verzerrt man eine Fläche, so bleibt ihre Euler-Charakteristik unverändert, im Gegensatz zur Gaußkrümmung an den einzelnen Punkten. Der Satz sagt aus, dass das Integral über die Krümmung, also die Gesamtkrümmung, unverändert bleibt.

Beispiele

Halbsphäre

Der Torus $\mathbb{T}$ hat die konstante Gaußkrümmung $0$ und der Rand des Torus ist die leere Menge. Daher entfallen die beiden Integralterme und es folgt $0=2\pi \chi (\mathbb {T} )$ . Da das Geschlecht des Torus ist und der Torus eine orientierbare Fläche ohne Rand ist, gilt auch aufgrund der Formel $2-2g$ , wobei das Geschlecht bezeichnet, die Gleichheit $\chi (\mathbb {T} )=0$ .
Die runde Sphäre mit Radius 1 hat in jedem Punkt die Gauß-Krümmung 1. Das Integral über die Gauß-Krümmung entspricht also ihrem Flächeninhalt, dieser beträgt $4\pi$ . Andererseits ist die Euler-Charakteristik 2, da man die Sphäre als Verklebung von zwei (runden) Flächen entlang einer Kante mit einer Ecke bekommt (also 2-1+1=2).
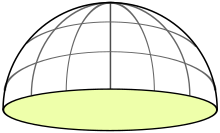
Die Halbsphäre mit Rand ist ebenfalls eine Fläche im Sinne des Satzes von Gauß-Bonnet. Aufgrund der Überlegungen aus dem Beispiel zur Sphäre wird klar, dass das Integral über die Gaußkrümmung in diesem Fall den Wert $2\pi$ annimmt. Der Rand der Halbsphäre ist gerade der $0$ , da sie ein Maß der Abweichung einer Kurve von einer geodätischen Kurve ist und jede Kurve auf dem Kreis eine geodätische Kurve sein muss. Die Euler-Charakteristik ist , da die Halbsphäre mit einem (sphärischen) Dreieck trianguliert werden kann. Dies entspricht dem, was der Satz von Gauß-Bonnet postuliert.

Flächen mit stückweise glattem Rand

Hat die Fläche eine stückweise differenzierbare Randkurven, so kann der Satz von Gauß-Bonnet auch für diesen Fall formuliert werden. In diesem Fall ergibt sich auf der linken Seite ein Zusatzterm.

Aussage

Sei wie zuvor eine kompakte und orientierbare zweidimensionale riemannsche Mannigfaltigkeit mit Rand $\partial M$ und sei die Gaußkrümmung in den Punkten von und mit k_g die geodätische Krümmung der Randkurve $\partial M$ . Dann gilt

$\int _{M}K\;dA+\int _{\partial M}k_{g}\;ds+\Sigma AW(\partial M)=2\pi \chi (M).$

Die Außenwinkel $AW$ sind definiert als die Winkel zwischen dem rechts- und dem linksseitigen Limes der Tangentialvektoren an den Knickstellen von $\partial M$ . Die Randkurve muss so orientiert sein, dass $N \times c'$ zur Fläche zeigt. Dabei ist der Normalenvektor der Fläche und der Tangentialvektor an die Randkurve.

Beispiel

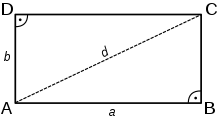
Rechteck, das durch Eintragen seiner Diagonale d trianguliert wurde

Ein Rechteck zusammen mit dem Standardskalarprodukt kann als Fläche mit stückweise glattem Rand im Sinne des Satzes verstanden werden. Um die Euler-Charakteristik zu bestimmen, kann man eine Diagonale im Rechteck eintragen und erhält zwei Dreiecke. Die Triangulierung besteht nun aus zwei Dreiecksflächen, fünf Kanten und vier Ecke. Laut der Definition der Euler-Charakteristik gilt also $\chi (M)=2-5+4=1$ . Da das Rechteck selbst als auch seine Randkurve die konstanten Krümmungen 0 aufweisen, sind die beiden Integralterme aus dem Satz jeweils 0 und die Summe der Außenwinkel beträgt $2\pi$ . Daher reduziert sich die Aussage des Satzes von Gauß-Bonnet in diesem Fall auf die Gleichheit $2\pi =2\pi$ .

Theorema elegantissimum

Diese von Gauß stammende Folgerung besagt, dass die Gesamtkrümmung $\textstyle \int_{\Delta}K\;dA$ eines einfach zusammenhängenden geodätischen Dreiecks gleich dessen Winkelexzess ist. Für den Spezialfall der 2-Sphäre sieht man über die Außenwinkelsumme eines infinitesimalen (also flachen) Dreiecks von $5\pi$ die Äquivalenz zum Satz von Gauß-Bonnet. Die Äquivalenz gilt allerdings – im zweidimensionalen Fall – auch allgemein, was mithilfe einer Triangulierung eingesehen werden kann, denn für sie gilt:

$2\pi\chi=2\pi(E-K+F)=2\pi(E-\frac 32F+F)=2\pi E-\pi F=\sum\varepsilon.$

Satz von Gauß-Bonnet-Chern

Der Satz von Gauß-Bonnet lässt sich auf Dimensionen verallgemeinern, was von André Weil und Carl B. Allendoerfer 1943 und mit neuen Beweisen von Shiing-Shen Chern 1944 gemacht wurde.

Sei eine kompakte orientierte riemannsche Mannigfaltigkeit mit gerader Dimension und sei der riemannsche Krümmungstensor. Da für diesen R(X,Y) = - R(Y,X) gilt, kann dieser als vektorwertige Differentialform

$R\in \mathcal{A}^2(M, \mathfrak{so}(TM))$

verstanden werden. Unter diesen Voraussetzungen gilt dann

$\chi (M) = \frac{1}{\sqrt{(2 \pi)^n}} \int_M \operatorname{Pf}(-R),$

wobei $\operatorname{Pf}$ die pfaffsche Determinante ist.

Mit dem Wissen, dass für den Fredholm-Index von $\mathrm{d} + \mathrm{d}^*$ die Gleichheit $\chi(M) = \operatorname{ind}(\mathrm{d} + \mathrm{d}^*)$ gilt, wobei $\mathrm {d}$ die äußere Ableitung ist, kann dieser Satz als Spezialfall des Atiyah-Singer-Indexsatzes verstanden werden. In diesem Zusammenhang bietet der Satz von Gauß-Bonnet-Chern also eine Möglichkeit zur Berechnung des topologischen Index des Operators $\mathrm{d} + \mathrm{d}^*$ .

Basierend auf einem Artikel in:

Wikipedia.de