
Kompakter Raum
Kompaktheit ist ein zentraler Begriff der mathematischen Topologie, und zwar eine Eigenschaft, die einem topologischen Raum zukommt oder nicht. Sie wird in vielen mathematischen Aussagen vorausgesetzt – oft auch in abgeschwächter Form als Lindelöf-Eigenschaft oder Parakompaktheit. Lokalkompaktheit ist im Falle von Hausdorff-Räumen ebenfalls eine abgeschwächte Bedingung. Eine kompakte Menge nennt man je nach Kontext auch Kompaktum oder kompakter Raum; dabei ist unerheblich, ob sie Teilmenge eines Oberraums ist.
Einfache Beispiele für kompakte Mengen sind abgeschlossene und
beschränkte
Teilmengen des Euklidischen
Raums
wie das Intervall
.
Einfache Gegenbeispiele bilden die nicht kompakten Mengen
(nicht beschränkt) oder
(nicht abgeschlossen).
Definition
Kompaktheit im Euklidischen Raum
Eine Teilmenge des euklidischen
Raums
heißt kompakt, wenn sie abgeschlossen
und beschränkt
ist. Für diese spezielle Definition gilt der Satz von
Heine-Borel:
- Eine Teilmenge des
ist genau dann kompakt, wenn jede offene Überdeckung der Teilmenge eine endliche Teilüberdeckung enthält.
Der Satz von Heine-Borel motiviert die folgende Verallgemeinerung der Definition der Kompaktheit auf topologische Räume.
Kompaktheit in topologischen Räumen
Ein topologischer
Raum
heißt kompakt, wenn jede offene
Überdeckung
besitzt.
Eine Teilmenge
eines topologischen Raums
heißt kompakt, wenn jede offene Überdeckung
eine endliche Teilüberdeckung
besitzt. Die beiden Begriffe sind kompatibel. Eine Teilmenge eines topologischen Raumes ist genau dann kompakt, wenn sie als topologischer Raum mit der Teilraumtopologie kompakt ist.
Einige Autoren, wie beispielsweise Nicolas Bourbaki, verwenden für die hier definierte Eigenschaft den Begriff quasikompakt und reservieren den Begriff kompakt für kompakte Hausdorff-Räume. Manche Autoren nennen die Kompaktheit zur klareren Abgrenzung von der Folgenkompaktheit auch Überdeckungskompaktheit.
Geschichte
Um das Jahr 1900 waren die folgenden Charakterisierungen kompakter Teilmengen
des
bekannt:
- Die Teilmenge
ist beschränkt und abgeschlossen.
- Jede Teilmenge von
mit unendlich vielen Elementen hat wenigstens einen Häufungspunkt. (Satz von Bolzano-Weierstraß)
- Jede Folge in
besitzt eine in
konvergente Teilfolge. (Satz von Bolzano-Weierstraß)
- Jede offene Überdeckung von
hat eine endliche Teilüberdeckung. (Satz von Heine-Borel)
Die erste Charakterisierung ist abhängig von der gewählten Metrik. Die anderen drei Charakterisierungen hingegen lassen sich auf beliebige topologische Räume übertragen und bieten somit eine Möglichkeit einen Kompaktheitsbegriff für topologische Räume zu definieren. Maurice René Fréchet nannte 1906 Teilmengen metrischer Räume kompakt, die die zweite Eigenschaft erfüllten. Diese Definition wurde später auf topologische Räume übertragen. Man nannte also die im heutigen Sinne abzählbar kompakten Räume damals kompakt. Pawel Sergejewitsch Alexandrow und Pawel Samuilowitsch Urysohn führten 1924 den heutigen Kompaktheitsbegriff im Sinne der vierten Eigenschaft ein. Räume, die diese Eigenschaft erfüllten, nannten sie bikompakt. Diese Kompaktheitsdefinition setzte sich allerdings erst um 1930 durch, als Andrei Nikolajewitsch Tichonow bewies, dass beliebige Produkte bikompakter Räume wieder bikompakte Räume ergeben. Dieses Resultat ist heute als Satz von Tychonoff bekannt. Für abzählbar kompakte und folgenkompakte Räume (Eigenschaft drei) gilt dies nicht.
Von Endlichkeit zu Kompaktheit
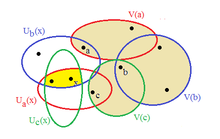
Ein wichtiger Grund für die Betrachtung kompakter Räume ist, dass sie in mancher Hinsicht als Verallgemeinerung von endlichen topologischen Räumen gesehen werden können, insbesondere sind auch alle endlichen Räume kompakt. Es gibt viele Ergebnisse, die sich leicht für endliche Mengen beweisen lassen, deren Beweise dann mit kleinen Änderungen auf kompakte Räume zu übertragen sind. Hier ein Beispiel:
Wir setzen voraus, dass
ein Hausdorff-Raum
ist,
ein Punkt aus
und
eine endliche Teilmenge von
,
die
nicht enthält. Dann können wir
und
durch Umgebungen
trennen: für jedes
aus
seien
und
disjunkte Umgebungen, die jeweils
bzw.
enthalten. Dann sind die Schnittmenge aller
und die Vereinigung aller
die benötigten Umgebungen von
und
.
Ist
nicht endlich, gilt der Beweis nicht mehr, da der Durchschnitt von unendlich
vielen Umgebungen keine Umgebung mehr sein muss. Für den Fall, dass
kompakt ist, lässt sich die Beweisidee aber wie folgt übertragen:
Wir setzen wieder voraus, dass
ein Hausdorff-Raum
ist,
ein Punkt aus
und
eine kompakte Teilmenge von
,
die
nicht enthält. Dann können wir
und
durch Umgebungen
trennen: für jedes
aus
seien
und
disjunkte offene Umgebungen, die jeweils
bzw.
enthalten. Da
kompakt ist und von den offenen Mengen
überdeckt wird, gibt es endlich viele Punkte
mit
.
Dann sind die Schnittmenge aller
und die Vereinigung aller
,
,
die benötigten Umgebungen von
und
.
Man sieht an diesem Beispiel, wie die Kompaktheit verwendet wird, um von möglicherweise unendlich vielen Umgebungen auf endlich viele zu kommen, mit denen dann der bekannte Beweis für endliche Mengen fortgeführt werden kann. Viele Beweise und Sätze über kompakte Mengen folgen diesem Muster.
Beispiele
Kompakte Räume
- Betrachtet man das geschlossene Einheits-Intervall
als Teilmenge von
versehen mit der Standardtopologie, so ist das Intervall ein kompakter, topologischer Raum. Ebenfalls kompakt sind die
-Kugeln und
-Sphären betrachtet als Teilmengen der
versehen mit der Standardtopologie für beliebige natürliche Zahlen
.
- Alle topologischen Räume mit endlicher Topologie, z.B. endliche Räume, sind kompakt.
- Für eine natürliche Zahl
betrachte die Menge
aller Folgen mit Werten aus
. Auf dieser Menge kann man eine Metrik
definieren, indem man
setzt, wobei
. Ist
, so sei
. Aus dem Satz von Tychonoff (siehe unten) folgt, dass der durch diese Metrik induzierte topologische Raum kompakt ist. Diese Konstruktion kann für jede endliche Menge durchgeführt werden, nicht nur für
. Der entstehende metrische Raum ist dabei sogar ultrametrisch. Es gilt folgendes:
- Ist
, dann ist die Abbildung
ein Homöomorphismus von
in die Cantor-Menge.
- Ist
eine Primzahl, dann ist die Abbildung
ein Homöomorphismus von
in die
-adischen ganzen Zahlen.
- Ist
- Das Spektrum eines beliebigen stetigen linearen Operators auf einem Hilbertraum ist eine kompakte Teilmenge der Komplexen Zahlen.
- Das Spektrum eines beliebigen kommutativen Ringes oder einer booleschen Algebra ist ein kompakter Raum mit der Zariski-Topologie.
- Weitere Beispiele kompakter Mengen aus der Funktionalanalysis erhält man durch den Satz von Banach-Alaoglu, den Satz von Kolmogorow-Riesz, den Satz von Arzelà-Ascoli oder das Kompaktheitskriterium von James.
Nicht kompakte Räume
- Die reellen
Zahlen
versehen mit der Standardtopologie sind nicht kompakt. Ebenfalls nicht kompakt sind das halboffene Intervall
, die ganzen Zahlen
oder die natürlichen Zahlen
betrachtet als Teilmengen von
. Versieht man jedoch beispielsweise
mit der trivialen Topologie
, so ist
kompakt. Ob eine Menge kompakt ist, hängt daher im Allgemeinen von der gewählten Topologie ab.
- Die abgeschlossene Einheitskugel des Raumes
der beschränkten reellen Zahlenfolgen (siehe Lp-Raum) ist nicht kompakt, obwohl sie abgeschlossen und beschränkt ist. Es gilt allgemein, dass die abgeschlossene Einheitskugel in einem normierten Raum genau dann kompakt ist, wenn die Dimension des Raums endlich ist.
Eigenschaften
- Das Bild einer kompakten Menge unter einer stetigen Funktion ist kompakt. Folglich nimmt eine reellwertige stetige Funktion auf einem nichtleeren Kompaktum ein globales Minimum und ein globales Maximum an.
- Eine stetige Funktion auf einem kompakten metrischen Raum ist gleichmäßig stetig. Diese Aussage ist auch als Satz von Heine bekannt.
- Jede Umgebung eines Kompaktums in einem uniformen Raum ist gleichmäßige Umgebung. Das heißt, es liegt mit einer Nachbarschaft in der Umgebung. Im metrischen Falle heißt dies, dass alle Punkte mit gleich großen Kugeln einer gewählten Größe innerhalb der Umgebung liegen. Die Nachbarschaft kann sogar so gewählt werden, dass das Komplement der Umgebung mit der Nachbarschaft außerhalb des Kompaktums mit der Nachbarschaft liegt.
- Jede unendliche Folge
von Elementen einer kompakten Menge
besitzt einen Häufungspunkt in
. Erfüllt
das erste Abzählbarkeitsaxiom, so existiert sogar eine in
konvergente Teilfolge
.
Die Umkehrung gilt jedoch nicht in jedem topologischen Raum, das heißt eine Teilmenge, in der jede Folge eine (in der Teilmenge) konvergente Teilfolge hat (eine solche Teilmenge heißt folgenkompakt, siehe unten), muss nicht kompakt sein. (Ein Beispiel bildet die Menge der abzählbaren Ordinalzahlenmit der Ordnungstopologie.)
- Eine abgeschlossene Teilmenge eines kompakten Raumes ist kompakt.
- Eine kompakte Teilmenge eines Hausdorff-Raumes ist abgeschlossen.
- Eine nicht-leere kompakte Teilmenge der reellen Zahlen hat ein größtes und ein kleinstes Element (siehe auch Supremum, Infimum).
- Für jede Teilmenge
des euklidischen Raumes
sind die folgenden drei Aussagen äquivalent (vergleiche Satz von Heine-Borel):
ist kompakt, das heißt jede offene Überdeckung von
hat eine endliche Teilüberdeckung.
- Jede Folge
in der Menge
hat eine in
konvergente Teilfolge (also mindestens einen Häufungspunkt).
- Die Menge
ist abgeschlossen und beschränkt.
- Ein metrischer Raum ist genau dann kompakt, wenn er vollständig und total beschränkt ist.
- Das Produkt einer beliebigen Klasse von kompakten Räumen ist kompakt in der Produkttopologie. (Satz von Tychonoff – dies ist äquivalent zum Auswahlaxiom)
- Ein kompakter Hausdorff-Raum ist normal.
- Jede stetige bijektive Abbildung von einem kompakten Raum auf einen Hausdorff-Raum ist ein Homöomorphismus.
- Ein metrischer Raum ist genau dann kompakt, wenn jede Folge in dem Raum eine konvergente Teilfolge mit ihrem Grenzwert in dem Raum hat.
- Ein topologischer Raum ist genau dann kompakt, wenn jedes Netz auf dem Raum ein Teilnetz hat, das einen Grenzwert in dem Raum hat.
- Ein topologischer Raum ist genau dann kompakt, wenn jeder Filter auf dem Raum eine konvergente Verfeinerung besitzt.
- Ein topologischer Raum ist genau dann kompakt, wenn jeder Ultrafilter auf dem Raum konvergiert.
- Ein topologischer Raum kann genau dann in einen kompakten Hausdorff-Raum eingebettet werden, wenn er ein Tychonoff-Raum ist.
- Jeder topologische Raum
ist ein dichter Unterraum eines kompakten Raumes, der höchstens einen Punkt mehr besitzt als
. (Siehe auch Alexandroff-Kompaktifizierung.)
- Ein metrisierbarer Raum
ist genau dann kompakt, wenn jeder zu
homöomorphe metrische Raum vollständig ist.
- Falls der metrische Raum
kompakt ist und eine offene Überdeckung von
gegeben ist, dann existiert eine Zahl
, so dass jede Teilmenge von
mit Durchmesser
in einem Element der Überdeckung enthalten ist. (Lemma von Lebesgue)
- Jeder kompakte Hausdorffraum lässt genau eine uniforme Struktur zu, die die Topologie induziert. Die Umkehrung gilt nicht.
- Falls ein topologischer Raum eine Subbasis hat, so dass jede Überdeckung des Raumes durch Elemente der Subbasis eine endliche Teilüberdeckung hat, so ist der Raum kompakt. (Alexanders Subbasis-Satz)
- Zwei kompakte Hausdorff-Räume
und
sind genau dann homöomorph, wenn ihre Ringe von stetigen reell-wertigen Funktionen
und
isomorph sind.
Andere Formen von Kompaktheit
Es gibt einige topologische Eigenschaften, die äquivalent zur Kompaktheit in metrischen Räumen sind, aber nicht äquivalent in allgemeinen topologischen Räumen:
- Folgenkompakt: Jede Folge hat eine konvergente Teilfolge.
- ω-beschränkt: Jede abzählbare Teilmenge ist in einer kompakten Teilmenge enthalten.
- Abzählbar
kompakt: Jede abzählbare offene Überdeckung hat eine endliche
Teilüberdeckung. (Oder, äquivalent, jede unendliche Teilmenge hat einen
-Häufungspunkt.)
- Pseudokompakt: Jede reell-wertige stetige Funktion auf dem Raum ist beschränkt.
- Schwach abzählbar kompakt: Jede unendliche Teilmenge hat einen Häufungspunkt.
- Eberlein-kompakt: Der Raum ist homöomorph zu einer schwach-kompakten Teilmenge eines Banachraums.
Während diese Konzepte für metrische Räume äquivalent sind, gibt es im Allgemeinen folgende Beziehungen:
- Kompakte Räume sind
-beschränkt.
-beschränkte Räume sind abzählbar kompakt.
- Folgenkompakte Räume sind abzählbar kompakt.
- Abzählbar kompakte Räume sind pseudokompakt und schwach abzählbar kompakt.
- Eberlein-kompakte Räume sind folgenkompakt.
Siehe auch
- Relativ kompakte Teilmenge (Kompaktheit des Abschlusses)
- Kompaktifizierung (Einbettung topologischer Räume in kompakte Räume)
- Schwach folgenkompakte Menge
- Vollständige algebraische Varietät (analoge Begriffsbildung für algebraische Varietäten)
Literatur
- Boto von Querenburg: Mengentheoretische Topologie (= Springer-Lehrbuch). 3., neu bearbeitete und erweiterte Auflage. Springer, Berlin u. a. 2001, ISBN 3-540-67790-9.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 24.10. 2021