
Häufungspunkt
In der Analysis ist ein Häufungspunkt einer Menge anschaulich ein Punkt, der unendlich viele Punkte der Menge in seiner Nähe hat. Ein Häufungspunkt einer Folge (seltener: „Verdichtungspunkt“ oder „Häufungswert“) ist ein Punkt, der Grenzwert einer Teilfolge ist. Beide Begriffe sind eng miteinander verwandt. Entsprechende, aber im Detail leicht unterschiedliche Definitionen gibt es in der Topologie. Der Begriff des Häufungspunkts spielt eine wichtige Rolle in der Mathematik.
Eine stärkere Bedingung gilt für einen Kondensationspunkt oder auch
-Häufungspunkt
(s.u.) einer Menge.
Häufungspunkte und Grenzwerte
Der Begriff Folgenhäufungspunkt ist eng verwandt mit dem Begriff Grenzwert. Der entscheidende Unterschied liegt darin, dass jede Folge höchstens einen Grenzwert haben kann, aber möglicherweise mehrere, vielleicht sogar unendlich viele Häufungspunkte.
Von einem Grenzwert wird gefordert, dass in jeder Umgebung fast alle Folgenglieder liegen. Bei einem Häufungspunkt müssen dies nur unendlich viele sein. Es können also nochmals „unendlich viele“ Folgenglieder für weitere Häufungspunkte übrig bleiben. Wenn eine Folge einen Grenzwert hat, dann ist dieser Grenzwert insbesondere auch ein Folgenhäufungspunkt. Wenn eine Folge in einem Hausdorff-Raum (also insbesondere jede Folge in einem metrischen Raum) mehrere Folgenhäufungspunkte hat, dann hat sie keinen Grenzwert.
Folgenhäufungspunkte und Mengenhäufungspunkte
Die Begriffe Folgenhäufungspunkt und Mengenhäufungspunkt sind eng miteinander verwandt, aber nicht genau gleichwertig. Das demonstriert folgendes Beispiel:

Die Folge
sei folgendermaßen definiert:
Die Folge a hat zwei Häufungspunkte. Die Teilfolge
konvergiert gegen 0, also ist 0 Folgenhäufungspunkt von
.
Die Teilfolge
konvergiert gegen 1, also ist auch 1 Folgenhäufungspunkt von
.
Die Menge der Folgenglieder von
ist definiert durch
Das heißt,
ist die Menge aller Folgenglieder, siehe Bildmenge von Funktionen. Nun
ist 0 ein Häufungspunkt der Menge
denn um jede ε-Umgebung gibt es noch Elemente
mit
,
die 1 jedoch nicht, da sich zum Beispiel in seiner Umgebung mit dem Radius
kein weiteres Element der Menge befindet.
Der Unterschied beruht darauf, dass ein Wert, der in einer Folge unendlich oft als Glied vorkommt, in der Menge trotzdem nur einmal gezählt wird. Jeder Mengenhäufungspunkt ist ein Folgenhäufungspunkt. Umgekehrt ist ein Folgenhäufungspunkt entweder ein Mengenhäufungspunkt, oder kommt unendlich oft als Folgenglied vor.
Häufungspunkt einer Folge
Definition
- Ein Punkt
heißt Häufungspunkt oder Häufungswert einer Folge von Punkten, falls in jeder noch so kleinen Umgebung des Punktes unendlich viele Folgenglieder liegen.
Diese Definition gilt zunächst für Folgen rationaler oder reeller Zahlen. Sie kann wortwörtlich ebenso in beliebigen, auch mehrdimensionalen, metrischen Räumen, allgemeiner noch in uniformen Räumen und darüber hinaus in allen topologischen Räumen verwendet werden. Dabei wird eine jeweils allgemeinere Definition des Umgebungsbegriffes verwendet.
Sofern die Topologie des Raumes nicht allzu 'verklumpt' ist, ist ein Punkt
bereits dann Häufungspunkt, wenn in jeder Umgebung von
ein von
verschiedenes Folgenglied liegt.
Eine Folge kann einen, mehrere, sogar unendlich viele Häufungspunkte besitzen, zwischen denen sie in ihrem Verlauf „hin- und herspringt“. Ebenso gibt es Folgen, die keinen Häufungspunkt besitzen.
In einem kompakten Raum besitzt jede unendliche Folge einen Häufungspunkt (zum Beispiel in einem beschränkten und abgeschlossenen Teilbereich des reellen Raumes).
Häufungspunkte und Grenzwerte
Der Grenzwert einer konvergenten Folge ist immer auch Häufungspunkt der Folge, denn per Definition enthält jede noch so kleine Umgebung des Grenzwertes alle bis auf endlich viele Folgenglieder. In metrischen Räumen und allgemeiner in Hausdorff-Räumen ist der Grenzwert einer konvergenten Folge eindeutig und ist auch der einzige Häufungspunkt der Folge. In allgemeineren topologischen Räumen kann eine Folge gleichzeitig sowohl einen Grenzwert besitzen als auch einen Häufungspunkt, der kein Grenzwert ist.
Teilfolgen
Hat eine Folge einen Grenzwert, so konvergieren alle Teilfolgen gegen diesen. Für einen Häufungspunkt ist es hinreichend, dass eine Teilfolge gegen den Häufungspunkt konvergiert. Jeder Häufungspunkt einer Teilfolge ist auch Häufungspunkt der Ausgangsfolge. Im Raum der reellen Zahlen (und allgemeiner in allen das erste Abzählbarkeitsaxiom erfüllenden topologischen Räumen) gibt es zu jedem Häufungspunkt eine Teilfolge, die gegen diesen Häufungspunkt konvergiert.
Limes superior und Limes inferior
Vorausgesetzt, die Menge der Häufungspunkte einer beschränkten reellen
Zahlenfolge sei nichtleer,
beschränkt
und außerdem abgeschlossen,
wird der Limes
superior (zu deutsch „oberer Limes“ oder „oberer Grenzwert“) als der größte
Häufungspunkt dieser Folge definiert, geschrieben .
Dabei gilt:
ist größter Häufungspunkt einer Folge
genau dann, wenn für jedes
im Intervall
unendlich viele, im sich anschließenden Intervall
dagegen höchstens endlich viele (weitere) Folgenglieder anzutreffen sind.
Analog wird der Limes
inferior (zu deutsch „unterer Limes“ oder „unterer Grenzwert“) als der
kleinste Häufungspunkt einer beschränkten reellen Zahlenfolge definiert. Es gilt
.
Limes superior und Limes inferior lassen sich auf die erweiterten reellen
Zahlen verallgemeinern und schließen dann für nach oben unbeschränkte Folgen
den Wert
und für nach unten unbeschränkte Folgen
als Häufungspunkte ein. Zur Unterscheidung werden
und
in diesem Zusammenhang oft als uneigentliche Häufungspunkte
bezeichnet.
Unter Einschluss der uneigentlichen Häufungspunkte existieren Limes superior und
Limes inferior dann nicht nur für beschränkte, sondern für alle beliebigen
reellen Zahlenfolgen.
Beispiele
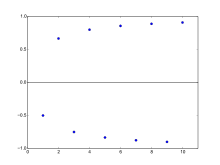
- Die konstante reellwertige Folge
hat 1 als einzigen Häufungspunkt. Die Elemente der Folge
springen zwischen +1 und −1 hin und her, und beide Punkte sind Häufungspunkte der Folge, obwohl es beispielsweise Umgebungen um +1 gibt, so dass unendlich viele Folgenglieder außerhalb der Umgebung liegen. Gleichzeitig konvergiert die Teilfolge der Elemente mit geradem Folgenindex gegen den oberen Häufungspunkt +1, und die Teilfolge der Elemente mit ungeradem Folgenindex konvergiert gegen den unteren Häufungspunkt −1.
- Die Folge
konvergiert gegen 0, und 0 ist dementsprechend der einzige Häufungspunkt der Folge. Das Beispiel zeigt, dass der Häufungspunkt der Folge selbst nicht in der Folge vorzukommen braucht.
- Die reellwertige divergente
Folge
hat keinen Häufungspunkt. Durch Hinzufügen eines „Punktes im Unendlichen“ (Einpunktkompaktifizierung) lässt sich die Menge der reellen Zahlen zu einem kompakten Raum erweitern, in dem der hinzugefügte Punkt der einzige Häufungspunkt der Folge ist.
- In einem mit der indiskreten Topologie versehenen Raum ist jeder Punkt des Raumes Häufungspunkt und sogar Grenzwert jeder Folge: Die indiskrete Topologie ist die gröbstmögliche Topologie, und in einem solchen Raum ist der ganze Raum selbst die einzige nichtleere offene Menge und somit die einzige als Umgebung infrage kommende Menge. In einem mit der diskreten Topologie versehenen Raum dagegen ist ein Punkt genau dann Häufungspunkt einer Folge, wenn er unendlich oft als Element der Folge auftaucht: Die diskrete Topologie ist die feinstmögliche Topologie, und in einem solchen Raum sind auch die einelementigen Teilmengen offen. Damit ist jede einelementige Teilmenge die kleinstmögliche Umgebung des in ihr enthaltenen Punktes.
- Die Folge
besitzt 1 und −1 als Häufungspunkt. Dies erkennt man auch gut an folgender Graphik, welches alle Folgenglieder dieser Folge zeigt:
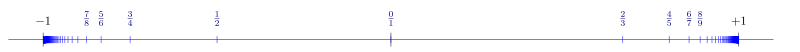
Häufungspunkte und Berührpunkte einer Menge
Definition
In einem topologischen
Raum
sei
ein Punkt der Grundmenge
und
eine Teilmenge von
.
Man bezeichnet
als Berührpunkt (auch Adhärenzpunkt) von
,
wenn in jeder Umgebung
von
mindestens ein Punkt von
liegt.
heißt Häufungspunkt von
,
wenn in jeder Umgebung
von
mindestens ein Punkt von
liegt, der von
verschieden ist.
Man kann Mengenhäufungspunkte also so charakterisieren, dass diese durch andere
Elemente der Menge beliebig genau approximiert werden können. Die Menge aller
Häufungspunkte einer Menge wird als Ableitung
der Menge bezeichnet. Die Menge aller Berührpunkte von
heißt Abschluss
von
und wird als
geschrieben.
In topologischen Räumen ist:
genau dann ein Häufungspunkt von
, wenn
,
- jeder Häufungspunkt ein Berührpunkt,
- jeder Punkt
ein Berührpunkt,
- jeder Berührpunkt, der in
liegt, auch ein Häufungspunkt von
.
In diesem Zusammenhang heißt
Häufungspunkt von
im engeren Sinne (oder eigentlicher Häufungspunkt),
wenn jede Umgebung von
unendlich viele gemeinsame Punkte mit
hat.
In einem T1-Raum sind die
Begriffe Häufungspunkt und Häufungspunkt im engeren Sinne
äquivalent, und jeder Punkt
ist unter der Voraussetzung, dass der Umgebungsfilter eines jeden Punktes des
Raumes eine höchstens abzählbare Basis hat, genau dann ein Häufungspunkt von
,
wenn es eine aus Punkten von
\
bestehende Folge gibt, die gegen
konvergiert.
Sei
der Umgebungsfilter
des Punktes
im topologischen Raum
.
Man nennt
den Verdichtungsgrad der Menge
im Punkt
.
Für jede Kardinalzahl
heißt
ein
-Häufungspunkt
von
,
wenn
.
Die
-Häufungspunkte
heißen maximale oder vollständige Häufungspunkte. Die
-Häufungspunkte
(lies Aleph-1-Häufungspunkte)
heißen Verdichtungs- oder Kondensationspunkte. Die Menge aller
Punkte in
,
die Kondensationspunkte einer Menge
sind, heißt Kondensation von
und wird mit
oder
bezeichnet. In polnischen
Räumen gilt für jede Menge
:
.
heißt isolierter
Punkt von
,
wenn er in
liegt, aber kein Häufungspunkt von
ist.
heißt unverdichtet, falls er kein Verdichtungspunkt von
ist. Mengen ohne isolierte Punkte heißen insichdicht. Mengen, die nur aus
isolierten Punkten bestehen, heißen isolierte Mengen. In einem T1-Raum sind die
abgeschlossene Hülle einer insichdichten Menge sowie die Vereinigung von
insichdichten Mengen insichdicht.
Die relativ offenen Teilmengen einer insichdichten Menge sind auch
insichdicht.
Die Vereinigung aller insichdichten Teilmengen von
heißt der insichdichte Kern von
.
Mengen, deren insichdichte Kerne leer sind, heißen separiert. Jede
isolierte Menge ist separiert, nicht aber umgekehrt.
In einem T1-Raum ist der
insichdichte Kern von
die bezüglich der Inklusion größte insichdichte Teilmenge von
.
Abgeschlossene insichdichte Mengen heißen perfekt. In polnischen Räumen
ist eine Menge
genau dann perfekt, wenn
.
Beispiel
Sei
eine Teilmenge der reellen
Zahlen.
besteht also aus einem links halboffenen Intervall
und einem einzelnen Punkt. Mit Ausnahme der
sind alle Elemente von
Häufungspunkte von
.
Die
ist isoliert, weil beispielsweise das offene Intervall
eine Umgebung von
ist, die keinen weiteren Punkt aus
enthält.
Zusätzlich ist auch die Null Häufungspunkt von .
Da das Intervall links offen ist, gibt es Punkte im Intervall, die beliebig nahe
an der Null liegen. Somit muss jede Umgebung der Null auch einen Punkt des
Intervalls enthalten. Aus gleichem Grund ist auch die
Häufungspunkt von
.
Hier wird deutlich, dass ein Häufungspunkt von
der Menge
angehören kann, aber nicht muss.
Andere Bezeichnungen
Zuweilen werden statt Häufungspunkt auch die Wörter Häufungswert,
-Punkt
oder Grenzpunkt
benutzt.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 30.11. 2020