Limes superior und Limes inferior

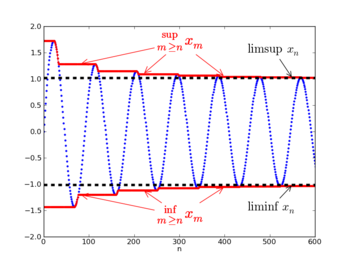
Limes superior und Limes inferior einer Folge: Die Folge x_n wird mit blauen Punkten dargestellt. Die beiden roten Kurven nähern sich dem Limes superior und Limes inferior der Folge an, die als gestrichelte schwarze Linien dargestellt sind.

In der Mathematik bezeichnen Limes superior bzw. Limes inferior einer Folge reeller Zahlen den größten bzw. kleinsten Häufungspunkt der Folge. Limes superior und Limes inferior sind ein partieller Ersatz für den Grenzwert, falls dieser nicht existiert.

Notation

Der Limes inferior wird im Folgenden mit $\liminf_{n\rightarrow\infty}$ bezeichnet, der Limes superior mit $\limsup_{n\rightarrow\infty}$ . Üblich sind als Bezeichnung auch $\varliminf_{n\rightarrow\infty}$ für den Limes inferior bzw. $\varlimsup_{n\rightarrow\infty}$ für den Limes superior.

Limes superior und Limes inferior für Folgen

Folgen reeller Zahlen

Definition

Sei $(x_n)_{n \in \N}$ eine Folge reeller Zahlen. Dann ist der Limes inferior von $(x_n)_{n \in \N}$ definiert als

$\liminf_{n\rightarrow\infty}x_n := \sup_{n\in \N}\,\inf_{k\geq n}x_k=\sup\{\inf\{x_k:k\geq n\}:n\in\N\}$

Analog ist der Limes superior von $(x_n)_{n \in \N}$ definiert als

$\limsup_{n\rightarrow\infty}x_n:= \inf_{n\in \N}\,\sup_{k\geq n}x_k=\inf\{\sup\{x_k:k\geq n\}:n\in\N\}.$

Dabei stehen $\inf$ und $\sup$ für Infimum und Supremum.

Eigenschaften

Als Elemente der erweiterten reellen Zahlen $\R\cup\lbrace-\infty,+\infty\rbrace$ existieren Limes inferior und Limes superior für jede Folge reeller Zahlen. Der Limes inferior und der Limes superior sind genau dann beide reelle Zahlen, wenn die Folge beschränkt ist. In diesem Fall erhält man aus der Existenz von Limes inferior und Limes superior den Satz von Bolzano-Weierstraß.

Für jedes $\epsilon >0$ liegen jeweils unendlich viele Folgenglieder im offenen Intervall

$(\limsup_{n\rightarrow\infty}x_n-\epsilon, \limsup_{n\rightarrow\infty}x_n+\epsilon) \text{ bzw. } (\liminf_{n\rightarrow\infty}x_n-\epsilon, \liminf_{n\rightarrow\infty}x_n+\epsilon).$

Außerdem erfüllen fast alle Folgenglieder

$x_n>\liminf_{n\rightarrow\infty}x_n-\epsilon$ bzw. $x_n<\limsup_{n\rightarrow\infty}x_n+\epsilon.$

Damit ist der Limes inferior der kleinste und der Limes superior der größte Häufungspunkt einer Folge und somit gilt

$\liminf_{n\rightarrow\infty}x_n\leq\limsup_{n\rightarrow\infty}x_n.$

Gleichheit liegt genau dann vor, wenn die Folge in den erweiterten reellen Zahlen konvergiert. In diesem Fall gilt

$\lim_{n\rightarrow\infty} x_n=\liminf_{n\rightarrow\infty}x_n=\limsup_{n\rightarrow\infty}x_n.$

Die Bezeichnung $\limsup$ bzw. $\liminf$ ist dadurch motiviert, dass

$\liminf_{n\rightarrow\infty}x_n=\lim_{n\rightarrow\infty}\left(\inf_{k\geq n}x_k\right)$ bzw. $\limsup_{n\rightarrow\infty}x_n=\lim_{n\rightarrow\infty}\left(\sup_{k\geq n}x_k\right).$

Die Grenzwerte existieren, da monotone Folgen in den erweiterten reellen Zahlen konvergent sind.

Da Häufungspunkte gerade die Grenzwerte konvergenter Teilfolgen sind, ist der Limes inferior die kleinste erweiterte reelle Zahl, gegen die eine Teilfolge konvergiert bzw. der Limes superior die größte.

Verallgemeinerung auf allgemeine Folgen

Sei eine partiell geordneten Menge und $f \colon \N\to M$ eine Folge. Um $\liminf_{n\rightarrow\infty}x_n$ und $\limsup _{n\rightarrow \infty }x_{n}$ genauso wie im Fall von reellen Folgen definieren zu können, müssen in die entsprechenden Suprema und Infima existieren. Dies ist zum Beispiel dann der Fall, wenn ein vollständiger Verband ist, so dass auch in diesem Fall jede Folge einen Limes inferior und einen Limes superior besitzt.

Limes superior und Limes inferior für Folgen reeller Funktionen

Für eine Folge reeller Funktionen $(f_n)_{n \in \N}$ , also $f_n\colon\R\rightarrow\R$ für alle $n\in \mathbb {N}$ , sind Limes inferior und Limes superior punktweise definiert, also

$(\liminf_{n\rightarrow\infty} f_n)(x)=\liminf_{n\to\infty}f_n(x) \text{ und } (\limsup_{n\rightarrow\infty} f_n)(x)=\limsup_{n\to\infty}f_n(x).$

Eine bekannte mathematische Aussage, die den Begriff des Limes inferior einer Funktionenfolge verwenden, ist das Lemma von Fatou.

Limes superior und Limes inferior von Mengenfolgen

→ Hauptartikel: Limes superior und Limes inferior von Mengenfolgen

Für eine beliebige Menge $\Omega$ bildet die Potenzmenge $P(\Omega)$ einen vollständigen Verband unter der durch die Teilmengenrelation definierten Ordnung. Sei $(A_{n})_{n\in \mathbb {N} }$ eine Folge von Teilmengen von $\Omega$ , also $A_n\subseteq \Omega$ für alle $n\in \mathbb {N}$ . Dann gilt

$\sup_{n\in \N} A_n= \bigcup_{n\in \N}A_n, \inf_{n\in \N} A_n=\bigcap_{n\in \N}A_n.$

Damit erhält man für Limes inferior und limes Superior

$\liminf_{n\rightarrow\infty} A_n={\bigcup_{n=1}^\infty}\left({\bigcap_{m=n}^\infty}A_m\right)$

und

$\limsup_{n\rightarrow\infty} A_n={\bigcap_{n=1}^\infty}\left({\bigcup_{m=n}^\infty}A_m\right).$

Der Limes inferior einer Folge $(A_{n})_{n\in \mathbb {N} }$ kann als die Menge aller Elemente aus $\Omega$ beschrieben werden, die in fast allen $A_{n}$ liegen, der Limes superior der Mengenfolge $(A_{n})_{n\in \mathbb {N} }$ als die Menge aller Elemente aus $\Omega$ , die in unendlich vielen $A_{n}$ liegen.

Der Limes superior von Mengen wird beispielsweise im Borel-Cantelli-Lemma verwendet. Außerdem lassen sich mit dem Limes inferior und superior konvergente Mengenfolgen definieren. Man sagt, die Folge $(A_{n})_{n\in \mathbb {N} }$ konvergiert gegen eine Menge , falls der Limes inferior und der Limes superior der Folge gleich sind. Eine Folge von Teilmengen einer Menge konvergiert genau dann, wenn es zu jedem einen Index N=N(x) gibt, so dass entweder $x\in A_n$ für alle $n\geq N$ oder $x\notin A_n$ für alle $n\geq N$ gilt.

Limes superior und Limes inferior von Funktionen

Sei $I\subseteq \R$ ein Intervall, $\xi$ ein innerer Punkt von und $f\colon I\to \R$ eine reellwertige Funktion. Dann sind Limes superior und Limes inferior jene Werte aus den erweiterten reellen Zahlen $\mathbb{R} \cup \{-\infty ,+\infty \}$ , die folgendermaßen definiert sind:

$\limsup_{x\to\xi} f(x)=\inf_{a>0} \sup f((\xi-a,\xi+a)\backslash\{\xi\})$ ,

$\liminf_{x\to\xi} f(x)=\sup_{a>0} \inf f((\xi-a,\xi+a)\backslash\{\xi\})$ .

$f((\xi-a,\xi+a))$ bezeichnet dabei die Bildmenge des offenen Intervalls $(\xi-a,\xi+a)$ , wobei so klein zu wählen ist, dass $(\xi-a,\xi+a)\subseteq I$ .

Analog zu einseitigen Grenzwerten werden ein einseitiger Limes superior und ein einseitiger Limes inferior definiert:

$\limsup_{x\to\xi+} f(x)=\inf_{a>0} \sup f((\xi,\xi+a))$ ,

$\liminf_{x\to\xi+} f(x)=\sup_{a>0} \inf f((\xi,\xi+a))$ ,

$\limsup_{x\to\xi-} f(x)=\inf_{a>0} \sup f((\xi-a,\xi))$ ,

$\liminf_{x\to\xi-} f(x)=\sup_{a>0} \inf f((\xi-a,\xi))$ .

Limes superior und Limes inferior von Funktionen werden beispielsweise bei der Definition der Halbstetigkeit verwendet.

Verallgemeinerung von Limes superior und Limes inferior

Definition

Sei ein beliebiger topologischer Raum, eine partiell geordnete Menge, in welcher zu jeder nichtleeren Teilmenge $A \subseteq M$ sowohl $\inf A$ als auch $\sup A$ existiert. trage die von dieser Ordnung induzierte Topologie. Sei weiter $f: V\rightarrow M$ , $V \subseteq T$ und $a \in T$ ein Häufungspunkt von (das heißt jede Umgebung von enthalte ein von verschiedenes Element aus ). Die Menge der Umgebungen von in werde mit $\mathfrak{U}(a)$ bezeichnet.

Definiere nun:

$\limsup_{x\to a} f(x):=\inf_{U\in\mathfrak{U}(a)} \sup_{x\in U\backslash\{a\}} f(x)$

$\liminf_{x\to a} f(x):=\sup_{U\in\mathfrak{U}(a)} \inf_{x\in U\backslash\{a\}} f(x)$

$\mathfrak{U}(a)$ darf hierbei durch eine beliebige Umgebungsbasis von ersetzt werden.

Eigenschaften

Es ist stets

$\liminf_{x\to a} f(x) \leq \limsup_{x\to a} f(x)$

Außerdem folgt aus der Gleichheit des Limes superior mit dem Limes inferior $\liminf_{x\to a} f(x) = \limsup_{x\to a} f(x)$ , dass $\lim_{x\to a} f(x)$ existiert und es gilt

$\lim_{x\to a} f(x) = \liminf_{x\to a} f(x) = \limsup_{x\to a} f(x)$

Beispiele

Für $T = \mathbb{N} \cup \{\infty\}$ , $V = \mathbb{N}$ , $M = \mathbb{R} \cup \{-\infty, \infty\}$ und $a = \infty$ erhält man die aus der Analysis bekannte Definition des Limes inferior und Limes superior einer Folge reeller Zahlen.
Für $T = \mathbb{N} \cup \{\infty\}$ , $V = \mathbb{N}$ , $M=\operatorname {Pot}(\Omega )$ und $a = \infty$ erhält man die Definition des Limes inferior und Limes superior für Mengenfolgen.

Basierend auf einem Artikel in:

Wikipedia.de