
Reellwertige Funktion
Eine reellwertige Funktion ist in der Mathematik eine Funktion, deren Funktionswerte reelle Zahlen sind. Eng verwandt ist der Begriff der reellen Funktion, der aber in der Literatur nicht eindeutig verwendet wird. Reellwertige Funktionen finden sich in fast allen Teilbereichen der Mathematik, insbesondere in der Analysis, der Funktionalanalysis und der Optimierung.
Definition
Reellwertige Funktion
Eine reellwertige Funktion ist eine Funktion
,
bei der die Zielmenge
die Menge der reellen
Zahlen ist. Die Definitionsmenge
ist dabei beliebig.
Reelle Funktion
Wie auch bei komplexwertigen und komplexen Funktionen wird der Begriff der reellen Funktion in der mathematischen Literatur nicht einheitlich verwendet. Teilweise ist dieser Begriff synonym zu einer reellwertigen Funktion, teilweise werden darunter auch nur Funktionen verstanden, deren Definitionsmenge eine Teilmenge der reellen Zahlen ist, also Funktionen
,
bei denen
ist.
Spezialfälle
Bei reellwertigen Funktionen werden an die Struktur der Definitionsmenge im
Allgemeinen keine Anforderungen gestellt. Soll die Definitionsmenge
eingeschränkt werden, wird dem Begriff „reellwertige Funktion“ ein
entsprechender Zusatz angehängt. So heißt beispielsweise eine Funktion
- reellwertige Funktion einer reellen Variablen, wenn
ist,
- reellwertige Funktion mehrerer reeller Variablen, wenn
mit
ist,
- reellwertige Funktion einer komplexen Variablen, wenn
ist,
- reellwertige Funktion mehrerer komplexer Variablen, wenn
mit
ist.
Wenn
Teilmenge eines reellen Vektorraums
ist, dann wird eine Funktion
auch (reellwertiges) Funktional
genannt.
Beispiele
- Die Funktion
ist eine reellwertige Funktion einer reellen Variablen.
- Die Funktion
ist eine reellwertige Funktion mehrerer reeller Variablen.
- Die Funktion
, die einer komplexen Zahl ihren Imaginärteil zuordnet, ist eine reellwertige Funktion einer komplexen Variablen.
- Ist
der Vektorraum der symmetrischen reellen Matrizen, so ist die Funktion
definiert durch
eine reellwertige Funktion.
- Die Nullfunktion
ist eine reellwertige Funktion, die auf beliebigen Mengen definiert ist. Sie weist jedem Element die Zahl Null zu.
Visualisierung
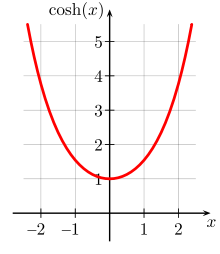
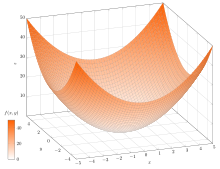
Der Graph
einer reellwertigen Funktion einer reellen Variablen kann visualisiert werden,
indem in ein zweidimensionales Koordinatensystem
die Punkte
eingetragen werden. Zur Darstellung reellwertiger Funktionen zweier reeller
Variablen werden in ein dreidimensionales Koordinatensystem die Punkte
eingetragen. Diese Darstellungen bilden bei stetigen
Funktionen eine Kurve oder Oberfläche ohne Sprünge. Bei Funktionen zweier
reeller Variablen werden teilweise auch Farben verwendet, um den Funktionswert
zu visualisieren. Reellwertige Funktionen einer komplexen Variablen können auf
die gleiche Weise wie reellwertige Funktionen zweier reeller Variablen
dargestellt werden. Der Imaginärteil und der Realteil werden dabei als erstes
und zweites Argument aufgefasst.
Eigenschaften
Algebraische Eigenschaften
Die Menge aller reellwertigen Funktionen über einer gegebenen Menge
bildet einen reellen Vektorraum,
der mit
,
oder
bezeichnet wird. Die Summe
zweier reellwertiger Funktionen
und
ist dabei definiert durch
für alle
und das Produkt
einer reellwertigen Funktion
mit einer reellen Zahl
durch
für alle .
Diese Vektorräume werden als reelle Funktionenräume
bezeichnet. Sie spielen eine wichtige Rolle in der linearen Algebra und
der Analysis. Mit der Addition und
der punktweisen Multiplikation definiert durch
für alle
bilden die reellwertigen Funktionen über der Menge
einen kommutativen
Ring. Mit allen drei Verknüpfungen bilden die reellwertigen Funktionen eine
reelle
Algebra.
Analytische Eigenschaften
Eine reellwertige Funktion
heißt beschränkt,
falls eine Schranke
existiert, sodass
für alle
ist. Die Menge der beschränkten reellwertigen Funktionen
bildet mit der Supremumsnorm
einen normierten
Raum. Da die reellen Zahlen vollständig
sind, handelt es sich hierbei sogar um einen Banachraum.
Eine Folge
reellwertiger Funktionen
mit
für
heißt gleichmäßig
beschränkt, wenn jedes Folgenglied eine beschränkte Funktion ist und die
Folge
eine beschränkte
Folge reeller Zahlen ist. Eine Folge reellwertiger Funktionen heißt punktweise
beschränkt, wenn für alle
die reelle Zahlenfolge
beschränkt ist. Eine gleichmäßig beschränkte Folge reellwertiger Funktionen
ist stets auch punktweise beschränkt, die Umkehrung muss jedoch nicht gelten.
Eine Folge reellwertiger Funktionen heißt gleichmäßig
konvergent gegen eine reellwertige Funktion ,
wenn
gilt. Entsprechend heißt eine Folge reellwertiger Funktionen punktweise
konvergent gegen eine reellwertige Funktion ,
wenn für alle
gilt. Auch hier folgt aus der gleichmäßigen Konvergenz die punktweise Konvergenz, jedoch nicht die Umkehrung. Weitergehende analytische Eigenschaften, wie Stetigkeit, Differenzierbarkeit oder Integrierbarkeit, erfordern auf der Definitionsmenge zumindest eine topologische, metrische oder maßtheoretische Struktur.
Ordnungseigenschaften
Nachdem die reellen Zahlen geordnet sind, lässt sich für reellwertige Funktionen die Halbordnung
definieren. Eine Folge
reellwertiger Funktionen
mit
heißt dann monoton
wachsend. Analog wird die Halbordnung
definiert und eine Folge reellwertiger Funktionen mit
ist dann monoton
fallend.
Verallgemeinerungen
Eine Verallgemeinerung der reellwertigen Funktionen bilden die reell-vektorwertigen
Funktionen. Dies sind Funktionen, die in den
abbilden. Noch allgemeiner sind die vektorwertigen
Funktionen, die in beliebige Vektorräume abbilden. Funktionen, die komplexe
Funktionswerte annehmen, werden komplexwertige
Funktionen genannt.
Literatur
- Otto Forster: Analysis 1. Differential- und Integralrechnung einer Veränderlichen. 11., erweiterte Auflage. Springer Spektrum, Wiesbaden 2013, ISBN 978-3-658-00316-6, doi: 10.1007/978-3-658-00317-3.
- Otto Forster: Analysis 2.
Differentialrechnung im
, gewöhnliche Differentialgleichungen. 10., verbesserte Auflage. Springer Spektrum, Wiesbaden 2013, ISBN 978-3-658-02356-0, doi: 10.1007/978-3-658-02357-7.
- Konrad Königsberger: Analysis 1. 6., durchgesehene Auflage. Springer-Verlag, Berlin Heidelberg New York 2004, ISBN 3-540-40371-X.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 26.12. 2021