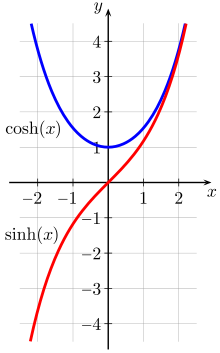
Sinus hyperbolicus und Kosinus hyperbolicus
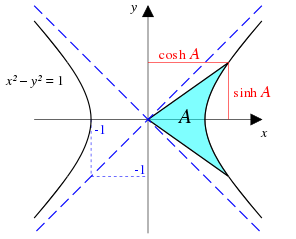
Sinus hyperbolicus und Kosinus hyperbolicus sind mathematische Hyperbelfunktionen,
auch Hyperbelsinus bzw. Hyperbelkosinus genannt; sie tragen die Symbole
bzw.
,
in älteren Quellen auch
und
.
Der Kosinus hyperbolicus beschreibt unter anderem den Verlauf eines an zwei
Punkten aufgehängten Seils. Sein Graph
wird deshalb auch als Katenoide
(Kettenlinie) bezeichnet.
Definitionen
- Sinus hyperbolicus
- Kosinus hyperbolicus
Die Funktionen sinh und cosh sind also der ungerade
bzw. gerade Anteil der Exponentialfunktion
().
Eigenschaften
| Sinus hyperbolicus | Kosinus hyperbolicus | |
|---|---|---|
| Definitionsbereich | ||
| Wertebereich | ||
| Periodizität | keine | keine |
| Monotonie | streng monoton steigend | |
| Symmetrien | Punktsymmetrie zum Ursprung | Achsensymmetrie zur Ordinate |
| Asymptotische
Funktionen |
||
| Nullstellen | keine | |
| Sprungstellen | keine | keine |
| Polstellen | keine | keine |
| Extrema | keine | Minimum bei |
| Wendestellen | keine |
Spezielle Werte
mit dem goldenen Schnitt
Uneigentliches Integral
Für den Kosinus hyperbolicus gilt insbesondere:
Umkehrfunktionen
Der Sinus hyperbolicus bildet
bijektiv
auf
ab und hat deshalb eine Umkehrfunktion,
die man Areasinus
hyperbolicus nennt.
Der Kosinus hyperbolicus bildet das Intervall
bijektiv auf das Intervall
und lässt sich eingeschränkt auf
also invertieren. Die Umkehrfunktion davon nennt man
Areakosinus
hyperbolicus
Beide Umkehrfunktionen, Areasinus hyperbolicus und Areakosinus hyperbolicus, lassen sich folgendermaßen mit Hilfe von elementareren Funktionen berechnen:
.
.
Ableitungen
Die Ableitung des Sinus hyperbolicus ist der Kosinus hyperbolicus und die Ableitung des Kosinus hyperbolicus ist der Sinus hyperbolicus:
Stammfunktionen
Zusammenhänge (zwischen den beiden Funktionen und anderen)
Additionstheoreme
insbesondere gilt für :
und für :
Summenformeln
Reihenentwicklungen
Die Taylorreihe des Sinus
hyperbolicus bzw. Kosinus hyperbolicus mit dem Entwicklungspunkt
lautet:
Produktentwicklungen
Komplexe Argumente
Mit
gilt:
So folgen beispielsweise die dritte und die vierte Gleichung auf folgende Weise:
Mit
gilt
Durch Koeffizientenvergleich folgt:
Anwendungen
Lösung einer Differentialgleichung
Die Funktion
mit
löst die Differentialgleichung
.
Kettenlinie
Ein homogenes Seil, das nur aufgrund seiner Eigenlast durchhängt, kann durch eine Kosinus-hyperbolicus-Funktion beschrieben werden. Eine derartige Kurve nennt man auch Kettenlinie, Kettenkurve oder Katenoide.
Lorentz-Transformation
Mit Hilfe der Rapidität
kann man die Transformationsmatrix
für eine spezielle
Lorentztransformation (auch Lorentz-Boost) in x-Richtung
folgendermaßen darstellen (für Transformationen in andere Richtungen ergeben
sich ähnliche Matrizen):
Man sieht eine große Ähnlichkeit zu Drehmatrizen; man erkennt so also gut die Analogie zwischen speziellen Lorentztransformationen in der vierdimensionalen Raumzeit und Drehungen im dreidimensionalen Raum.
Kosmologie
Der Sinus hyperbolicus tritt auch in der Kosmologie auf. Die zeitliche Entwicklung des Skalenfaktors in einem flachen Universum, das im Wesentlichen nur Materie und Dunkle Energie enthält (was ein gutes Modell für unser tatsächliches Universum ist), wird beschrieben durch
,
wobei
eine charakteristische Zeitskala ist.
ist dabei der heutige Wert des Hubble-Parameters,
der Dichteparameter
für die Dunkle Energie. Die Herleitung dieses Ergebnisses findet man bei den Friedmann-Gleichungen.
Bei der Zeitabhängigkeit des Dichteparameters der Materie tritt dagegen der
Kosinus hyperbolicus auf:
.
Siehe auch


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 15.07. 2025