Gerade und ungerade Funktionen
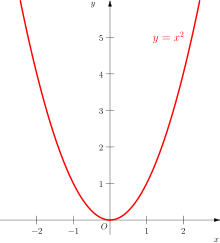
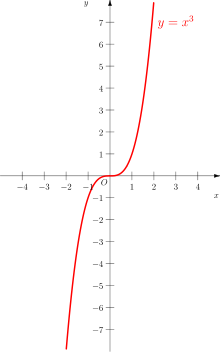
Gerade und ungerade Funktionen sind in der Mathematik zwei Klassen von Funktionen, die bestimmte Symmetrieeigenschaften aufweisen. Eine reelle Funktion ist genau dann gerade, wenn ihr Funktionsgraph achsensymmetrisch zur y-Achse ist, und ungerade, wenn ihr Funktionsgraph punktsymmetrisch zum Koordinatenursprung ist.
Definition
Eine reelle Funktion
mit einem bezüglich der Null
symmetrischen Definitionsbereich
heißt gerade, wenn für alle Argumente
gilt, und sie heißt ungerade, wenn für alle
gilt. Anschaulich ist eine reelle Funktion genau dann gerade, wenn ihr Funktionsgraph achsensymmetrisch zur y-Achse ist, und ungerade, wenn ihr Funktionsgraph punktsymmetrisch zum Koordinatenursprung ist.
Beispiele
Gerade Funktionen
- die konstante
Funktion
- die Betragsfunktion
- die Normalparabel
- die Kosinusfunktion
- die Sekansfunktion
- die Gaußsche
Glockenkurve
Ungerade Funktionen
- die Vorzeichenfunktion
- die identische
Funktion
- die kubische
Funktion
- die Sinusfunktion
- die Tangensfunktion
- die Gaußsche
Fehlerfunktion
Die einzige Funktion, die gleichzeitig gerade und ungerade ist, ist die Nullfunktion .
Allgemeinere Beispiele
- Eine Potenzfunktion
-
- ist für
genau dann gerade, wenn der Exponent
gerade ist, und genau dann ungerade, wenn der Exponent
ungerade ist.
- Eine Polynomfunktion
-
- ist genau dann gerade, wenn alle ungeradzahligen Koeffizienten
gleich null sind, und genau dann ungerade, wenn alle geradzahligen Koeffizienten
gleich null sind.
-
- ist genau dann gerade, wenn alle Koeffizienten
sind, und genau dann ungerade, wenn alle Koeffizienten
sind.
Zerlegung
Es gibt auch Funktionen, die weder gerade noch ungerade sind, zum Beispiel
die Funktion .
Jede Funktion lässt sich jedoch als Summe einer geraden und einer ungeraden
Funktion schreiben, das heißt
,
wobei
den geraden Anteil der Funktion und
den ungeraden Anteil der Funktion darstellt. Diese Zerlegung einer Funktion in gerade und ungerade Komponenten ist eindeutig, d.h. es gibt keine andere Möglichkeit, eine Funktion in gerade und ungerade Komponenten zu zerlegen. Dies folgt aus den Tatsachen, dass die Mengen aller geraden/ungeraden Funktionen einen Untervektorraum des Raums aller Funktionen bilden und die einzige Funktion, die sowohl gerade als auch ungerade ist, die Nullfunktion ist.
Eigenschaften
Algebraische Eigenschaften
- Jedes Vielfache einer geraden bzw. ungeraden Funktion ist wieder gerade bzw. ungerade.
- Die Summe zweier gerader Funktionen ist wieder gerade.
- Die Summe zweier ungerader Funktionen ist wieder ungerade.
- Das Produkt zweier gerader Funktionen ist wieder gerade.
- Das Produkt zweier ungerader Funktionen ist gerade.
- Das Produkt einer geraden und einer ungeraden Funktion ist ungerade.
- Der Quotient zweier gerader Funktionen ist wieder gerade.
- Der Quotient zweier ungerader Funktionen ist gerade.
- Der Quotient einer geraden und einer ungeraden Funktion ist ungerade.
- Die Komposition einer beliebigen Funktion mit einer geraden Funktion ist gerade.
- Die Komposition einer ungeraden Funktion mit einer ungeraden Funktion ist ungerade.
Analytische Eigenschaften
- Im Nullpunkt hat (sofern dieser im Definitionsbereich enthalten ist) jede ungerade Funktion den Funktionswert Null.
- Die Ableitung einer geraden differenzierbaren Funktion ist ungerade, die Ableitung einer ungeraden differenzierbaren Funktion gerade.
- Das bestimmte
Integral einer ungeraden stetigen Funktion
ergibt
, wenn die Integrationsgrenzen symmetrisch um den Nullpunkt liegen.
- Die Taylor-Reihe
mit dem Entwicklungspunkt
einer geraden (ungeraden) Funktion enthält nur gerade (ungerade) Potenzen.
- Die Fourier-Reihe einer geraden (ungeraden) Funktion enthält nur Kosinus- (Sinus-)Terme.
Verallgemeinerungen
Allgemeiner definiert man in der Algebra
durch obige Definition auch gerade und ungerade Funktionen
zwischen zwei Mengen
und
,
auf denen eine Verknüpfung
mit additiv
Inversem gegeben ist, beispielsweise (additive) Gruppen, Ringe, Körper oder Vektorräume. Auf diese Weise
lassen sich beispielsweise auch gerade und ungerade komplexe Funktionen
oder gerade und ungerade vektorwertige
Funktionen definieren.
In der mathematischen Physik wird das Konzept der geraden und ungeraden Funktionen durch den Begriff der Parität verallgemeinert. Diese ist vor allem für Wellenfunktionen etwa in der Quantenmechanik von Bedeutung.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 07.08. 2022