
Komposition (Mathematik)
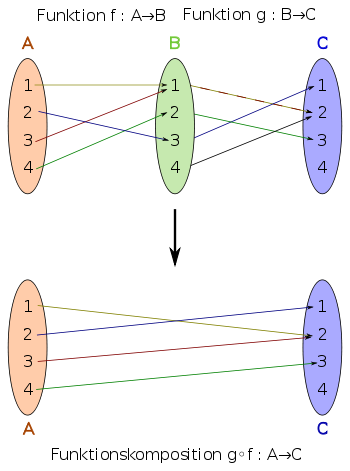
Der Begriff Komposition bedeutet in der Mathematik
meist die Hintereinanderschaltung von Funktionen,
auch als Verkettung, Verknüpfung oder
Hintereinanderausführung bezeichnet. Sie wird meist mit Hilfe des Verkettungszeichens
notiert.
Die Darstellung einer Funktion als Verkettung zweier oder mehrerer, im Allgemeinen einfacherer Funktionen ist zum Beispiel in der Differential- und Integralrechnung wichtig, wenn es darum geht, Ableitungen mit der Kettenregel oder Integrale mit der Substitutionsregel zu berechnen.
Der Begriff Komposition kann von Funktionen auf Relationen und partielle Funktionen verallgemeinert werden.
Definition
Seien
beliebige Mengen
und
sowie
Funktionen, so heißt die Funktion
die Komposition von
und
.
Der Ausdruck „
“
wird als „
verknüpft mit
“,
„
komponiert mit
“,
„
nach
“
oder „
Kringel
“
gelesen.
Es ist dabei zu beachten, dass die zuerst angewandte Abbildung rechts steht, im
Gegensatz zum Diagramm, wo sie links steht:
Abweichende Schreibweisen
Eine alternative Schreibweise für
ist
,
wobei man dies nicht mit dem Produkt
der Funktionen
verwechseln darf, bei dem das Multiplikationszeichen ebenfalls oft weggelassen
wird.
Es gibt auch wenige Autoren, die
nach
als
mit
schreiben, die Funktionen also von links nach rechts auswerten. Welche
Reihenfolge gewählt wurde, lässt sich oft an einem Beispiel des Autors
nachvollziehen. Daneben existiert auch die Notation, bei der das Funktionssymbol
rechts vom Argument geschrieben wird, also
(oder auch
)
anstelle von
.
Dann ist die Auswertung von links nach rechts naheliegend, also
(hauptsächlich im Kontext von (rechten) Gruppenoperationen
verbreitet).
Beispiele
Man betrachte die folgenden Funktionen, für die als Definitions- und
Wertemenge die Menge
der reellen Zahlen oder eine
Teilmenge davon angenommen wird. Ist die Funktion
durch
und die Funktion
durch
gegeben, so ergibt die Verkettung von
und
die Funktion
mit
.
Umgekehrt lässt sich die durch
definierte Funktion als
darstellen, wobei
sind.
Eigenschaften
Assoziativität
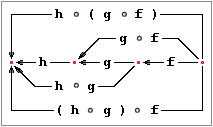
Die Komposition von Funktionen ist assoziativ.
Kommt nämlich zu den obigen Funktionen
und
noch eine Funktion
hinzu, dann definiert sowohl
wie
eine Funktion ,
die beide dieselben Werte produzieren, es gilt also:
für alle ;
mit der Folge, dass die Klammern weggelassen werden können. Recht eigentlich ist
diese Assoziativität nur eine notationelle Angelegenheit, denn die
Auswertungsreihenfolge ist in beiden Fällen dieselbe: sie ist im Ausdruck
formuliert und beginnt immer bei der innersten Klammer
,
rechts mit der Anwendung von
auf den Operanden
und schreitet nach links fort.
Identische Abbildungen
Die identische
Abbildung verhält sich bei der Komposition neutral, für eine Funktion
gilt also:
,
wobei
und
die jeweiligen Identitäten auf den Mengen
und
darstellen.
Injektivität, Surjektivität, Bijektivität
Wichtige Eigenschaften, die eine Funktion
besitzen kann, sind
- Injektivität
(kein Element in
wird mehrfach angenommen),
- Surjektivität
(jedes Element in
wird angenommen),
- Bijektivität
(jedes Element in
wird angenommen, und keins wird mehrfach angenommen).
Jede dieser Eigenschaften überträgt sich auf die Verkettung, es gilt also:
- Die Komposition injektiver Funktionen ist injektiv.
- Die Komposition surjektiver Funktionen ist surjektiv.
- Die Komposition bijektiver Funktionen ist bijektiv.
Umgekehrt gilt: Ist eine Verkettung
- injektiv, so ist
injektiv.
- surjektiv, so ist
surjektiv.
- bijektiv, so ist
injektiv und
surjektiv.
Kommutativität
Auch wenn Definitions- und Wertemenge jeweils übereinstimmen, ist die
Komposition von Funktionen normalerweise nicht kommutativ. Beispielsweise
gilt für die Funktionen
und
:
Iterationen
kommutieren generell, so auch die Identität und die Umkehrfunktion, so
vorhanden. Ansonsten kommt eine kommutative Komposition nur bei ganz speziell
gewählten Kombinationen von Funktionen vor. Beispiele dazu mit
als Definitions- und Wertemenge:
und
ergeben
und
ergeben
und
ergeben
Iteration
Ist
eine Abbildung einer Menge in sich selbst, dann kann man diese Funktion mit sich
selbst verketten und erhält die Funktion
,
die wiederum eine Funktion
ist. Wie bei assoziativen Operationen üblich kann nun induktiv für
jede natürliche
Zahl
die
-te
Iteration
von
erklärt werden durch:
Außerdem setzt man
,
mit der identischen
Abbildung
als dem neutralen
Element der Verkettung.
wird als
-te
Iterierte (oft auch als
-te
Potenz) von
bezeichnet.
Falls auf
eine Multiplikation definiert ist, darf die Iteration (der Verkettung) nicht mit
der Exponentiation
(Iteration der Multiplikation) verwechselt werden:
kann in diesem Fall auch den Ausdruck
bezeichnen (siehe dazu auch den §
Schreibweise).
Ist
bijektiv, dann existiert die Umkehrfunktion
,
und die negativen Iterationen
sind definiert durch:
Beispiele
Sei
die Menge der positiven reellen Zahlen und
gegeben durch
.
Dann gilt:
Algebraische Strukturen
Wird die Menge
aller Funktionen aus einer gegebenen Menge
in sich selbst betrachtet, so definiert die Komposition eine innere zweistellige
Verknüpfung auf
,
bezüglich der
(mit der identischen Abbildung als neutralem Element) ein Monoid ist.
Werden nur bijektive
Funktionen herangezogen, ist das Monoid sogar eine Gruppe mit der
jeweiligen Umkehrfunktion
als inversem
Element. Ist dann die Menge
endlich mit
Elementen ist, handelt es sich um die symmetrische
Gruppe
.
Strukturverträgliche Abbildungen
In der Mathematik betrachtet man oft Mengen mit einer zusätzlichen Struktur sowie Abbildungen, die mit dieser Struktur verträglich sind, zum Beispiel
- lineare Abbildungen zwischen Vektorräumen
- stetige Abbildungen zwischen topologischen Räumen
- Gruppenhomomorphismen zwischen Gruppen
Wünschenswert ist nun, dass die Strukturverträglichkeit bei der Komposition erhalten bleibt, und in der Tat gilt in den Beispielen:
- Die Komposition linearer Abbildungen ist linear.
- Die Komposition stetiger Abbildungen ist stetig.
- Die Komposition von Gruppenhomomorphismen ist ein Gruppenhomomorphismus.
Diese Überlegungen führen zur Kategorientheorie, bei der man sogar davon abstrahiert, dass es sich um Abbildungen handelt, und nur noch die Assoziativität sowie die Eigenschaft der Identitäten für die Komposition fordert.
Komposition von Relationen
Zu einer Funktion
ist der Funktionsgraph
eine Relation
.
Bezüglich der Komposition von Funktionen gilt dann (unter Verwendung der Infixnotation):
.
Diese Beobachtung führt zur Definition der Komposition von zweistelligen
Relationen
und
:
Die Relation
ist gegeben durch
.
Bei der Komposition von Relationen wird also immer die Reihenfolge von rechts nach links eingehalten.
Beispiel
sei die Menge der Punkte,
die Menge der Geraden und
die Menge der Ebenen
im dreidimensionalen Raum. Die Relationen
und
seien festgelegt durch:
der Punkt
liegt auf der Geraden
die Gerade
ist in der Ebene
enthalten
Für die Komposition
gilt dann:
der Punkt
liegt in der Ebene
Eigenschaften
- Die Komposition von Relationen ist assoziativ.
- Bezeichnet
die identische Relation auf einer Menge
, also die Menge aller Paare
, dann gilt für jede Relation
:
- Ist
eine Relation auf einer Menge
, dann sind also auch alle Potenzen
(mit
) definiert. Diese Potenzen werden zum Beispiel bei der Definition der reflexiv-transitiven Hülle verwendet. Eine Relation
mit
heißt transitiv.
Abweichende Notation in der Physik
In der Physik und anderen
Naturwissenschaften ist es üblich, die Verkettung einer Funktion mit der
"äußeren Funktion" zu identifizieren: .
Aufgrund dieser Notation entstehen in physikalischer Literatur teilweise
Gleichungen, die auf den ersten Blick nach gängigen mathematischen Konventionen
falsch oder sinnlos sind, etwa
,
wobei
der Ortsvektor des Punktes
ist und
seine euklidische Länge.
Diese Gleichung ist, mathematisch gesehen, im Prinzip falsch, da nach der linken
Seite der Gleichung
eine Funktion
darstellt (setzt man doch in
ein Element
ein), auf der rechten Seite
offenbar als Definitionsbereich eine Teilmenge der reellen Zahlen aufweist, also
,
da man in
die skalare
Größe
einsetzt. Gemeint ist mit dieser intuitiven
Gleichung jedoch, dass (für
einen betrachteten Spezialfall) die physikalische Größe
(in diesem Fall ein Potential),
das im Allgemeinen eine Funktion des Ortes ist, mit einer Funktion beschrieben
werden kann, die nur vom Abstand des Ortes
vom Nullpunkt abhängt. Eine mathematisch „saubere“ Formulierung dieser Aussage
würde etwa lauten:
ist also eine Verkettung aus der skalaren Funktion
und der euklidischen Norm
:
.
Wir erhalten die obige, intuitive Schreibweise dieser Gleichung, indem wir
zunächst die Verkettung
symbolisch mit der äußeren Funktion
identifizieren und diese wiederum mit dem Potenzial
.
Vorteile der Notation sind intuitiv verständliche Schreibweisen und eine geringe
Anzahl von verschiedenen Symbolen. Ein typisches Beispiel einer Funktion, die
die obige Gleichung erfüllt, sind Zentralpotenziale
der Form
die u.a. in der Elektrostatik
verwendet werden.
ist in diesem Fall eine Verkettung der skalaren Funktion
mit
mit der euklidischen Norm:


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 24.09. 2022