Potenz (Mathematik)

Die Schreibweise einer Potenz: ${\text{Potenzwert}}={\text{Basis}}^{\text{Exponent}}$

Eine Potenz (von lateinisch potentia ‚Vermögen, Macht‘) ist das Ergebnis des Potenzierens (der Exponentiation), das wie das Multiplizieren seinem Ursprung nach eine abkürzende Schreibweise für eine wiederholte mathematische Rechenoperation ist. Wie beim Multiplizieren ein Summand wiederholt zu sich selbst addiert wird, so wird beim Potenzieren ein Faktor wiederholt mit sich selbst multipliziert. Dabei heißt die Zahl, die zu multiplizieren ist, Basis. Wie oft diese Basis als Faktor auftritt, wird durch den Exponenten angegeben. Man schreibt:

${\text{Potenzwert}}={\text{Basis}}^{\text{Exponent}}$

Definition

Man spricht $a^{n}$ als a hoch n, n-te Potenz von a, a zur n-ten Potenz oder kurz a zur n-ten aus. Im Fall n=2 ist auch a (zum) Quadrat üblich.

heißt Basis (oder Grundzahl>), heißt Exponent (oder Hochzahl) der Potenz $a^{n}$ . Das Ergebnis heißt Potenz oder Wert der Potenz.

Die Definitionsmengen sowohl auf seiten der Exponenten wie auf seiten der Basen werden im Folgenden Schritt für Schritt erweitert.

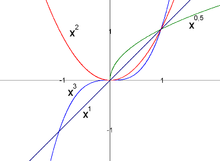
Natürliche Exponenten

Die Potenz $a^{n}$ wird für reelle oder komplexe Zahlen (allgemeiner Elemente eines beliebigen multiplikativen Monoids) und natürliche Zahlen durch

${\begin{matrix}a^{n}:=\underbrace {{a\cdot a\cdot a\dotsm a}}_{{{n\ {\mathrm {Faktoren}}}}}\end{matrix}}$

definiert. Diese Definition gilt nur für $n=1,2,3,\dotsc$ Damit die aus ihr (ebenfalls nur für $n=1,2,3,\dotsc$ ) folgende Identität $a\cdot a^{n}=a^{{n+1}}$ auch noch für n=0 gilt, wird $a^{0}:=1$ festgelegt. (Anmerkungen zum Fall a = 0 siehe unten.)

Potenzfunktionen mit positivem Exponenten graphisch

Potenzfunktionen mit negativem Exponenten graphisch

Die folgende Modifikation erleichtert die Behandlung des Sonderfalles n = 0 :

Die Potenzschreibweise bedeutet „Multipliziere die Zahl 1 mit der Grundzahl so oft, wie der Exponent angibt“, also

${\begin{matrix}a^{n}=1\cdot \underbrace {{a\cdot a\cdot a\dotsm a}}_{{{n\ {\mathrm {Faktoren}}}}}.\end{matrix}}$

Der Exponent 0 sagt aus, dass die Zahl 1 keinmal mit der Grundzahl multipliziert wird und allein stehen bleibt, sodass man das Ergebnis 1 erhält.

${\begin{aligned}a^{2}&=1\cdot a\cdot a\\a^{1}&=1\cdot a\\a^{0}&=1\end{aligned}}$

Bei negativer Basis und geradzahligem Exponenten ist die Potenz positiv:

$(-|a|)^{{2n}}=|a|^{{2n}}$

Bei negativer Basis und ungeradzahligem Exponenten ist die Potenz negativ:

$(-|a|)^{{2n+1}}=-|a|^{{2n+1}}$

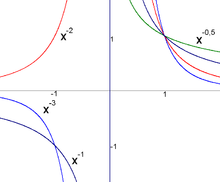
Ganze negative Exponenten

Negative Exponenten bedeuten, dass man die zur Multiplikation inverse Operation (Division) durchführen soll. Also „Dividiere die Zahl 1 durch die Grundzahl so oft, wie der Betrag des Exponenten angibt“.

${\begin{matrix}a^{{-n}}=1:\underbrace {{a:a:a:\dotsb :a}}_{{{n\ {\mathrm {Divisoren}}}}}\end{matrix}}$

Für eine reelle Zahl und eine natürliche Zahl definiert man also:

$a^{{-n}}:={\frac {1}{a^{n}}},\quad a\neq 0$

Die analoge Definition wird auch in allgemeinerem Kontext angewandt, wann immer eine Multiplikation und inverse Elemente zur Verfügung stehen, beispielsweise bei invertierbaren Matrizen.

Rationale Exponenten

Sei eine rationale Zahl mit der Bruchdarstellung $q={\tfrac mn}$ mit $m\in {\mathbb {Z}},\ n\in {\mathbb {N}}$ . Für beliebige positive reelle definiert man:

$a^{q}=a^{{{\tfrac mn}}}:={\sqrt[ {n}]{a^{m}}}$ $\qquad$ (oder, was äquivalent ist, $a^{{{\tfrac mn}}}:=({\sqrt[ {n}]a})^{m}$ )

Zum Beispiel gilt:

$2^{3,1}=2^{31/10}={\sqrt[{10}]{2^{31}}}=({\sqrt[{10}]{2}})^{31}$

Der Wert der Potenz hängt nicht davon ab, welche Bruchdarstellung man gewählt hat.

Dieselbe Definition gilt auch für a = 0 . Daraus folgt, dass $0^{q}=0$ für q>0 gilt und dass $0^{q}$ für q<0 nicht existiert.

Wenn man Wurzeln aus negativen Zahlen mit ungeraden Wurzelexponenten zulässt, dann kann man diese Definition auf negative Basen und solche rationale Exponenten erweitern, deren gekürzte Bruchdarstellungen ungerade Nenner haben. Dazu gehören auch Potenzen mit negativen Basen und ganzen Exponenten, weil die Nenner in diesem Fall gleich sind.

Für den Fall a<0 kann man bei Berechnungen von $a^{q}$ alle Bruchdarstellungen $q={\tfrac mn}$ mit ungeraden benutzen. Aber bei Benutzung von Bruchdarstellungen mit geraden können Fehler entstehen. Zum Beispiel gilt:

$-2=(-8)^{{1/3}}={\sqrt[ {3}]{-8}}={\sqrt[ {9}]{(-8)^{3}}}\neq {\sqrt[ {6}]{(-8)^{2}}}=2$

Reelle Exponenten

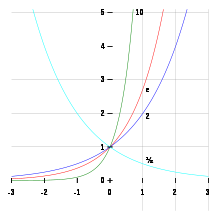
Exponentialfunktionen 0,5^x, 2^x, e^x und 10^x

Ist a>0 , eine beliebige reelle Zahl und $(q_{n})$ eine Folge rationaler Zahlen, die gegen konvergiert, so definiert man:

$a^{r}:=\lim _{{n\to \infty }}a^{{q_{n}}}$

Diese Definition ist korrekt, d.h., der Grenzwert existiert immer und hängt nicht von der Auswahl der Folge $(q_{n})$ ab.

Zum Beispiel ist $2^{{\pi }}$ gleich dem Grenzwert der Folge $2^{3},\,2^{3{,}1},\,2^{3{,}14},\,\dotsc .$

Die Definition lässt sich nicht auf den Fall a<0 erweitern, da in diesem Fall der Grenzwert nicht zu existieren braucht bzw. für verschiedene Wahlen der Folge $(q_{n})$ sich verschiedene Grenzwerte ergeben.

Eine andere Definition ist über die natürliche Exponentialfunktion und den natürlichen Logarithmus möglich:

$a^{r}=\operatorname {exp}(r\ln a)$

Dazu kann die Exponentialfunktion über ihre Reihenentwicklung definiert werden:

$\operatorname {exp}(x)=\sum _{{n=0}}^{\infty }{\frac {x^{n}}{n!}}$ >

Insgesamt sind somit die Potenzen mit nichtnegativen Basen für alle reellen Exponenten definiert. Im Unterschied dazu sind die Potenzen mit negativen Basen nur für solche rationalen Exponenten definiert, deren gekürzte Bruchdarstellungen ungerade Nenner haben. Alle Potenzen mit negativen Basen und ganzen Exponenten gehören dazu. Potenzen negativer Zahlen mit anderen reellen Exponenten lassen sich im Bereich der komplexen Zahlen definieren, sind allerdings nicht reellwertig.

Technische Schreibweisen

Wenn hochgestelltes Schreiben nicht möglich ist (zum Beispiel in einem ASCII-Text), verwendet man oft die Schreibweise a^b (beispielsweise in Algol 60, in TeX-Quellcode oder in Computeralgebrasystemen wie Maple), gelegentlich auch a**b (beispielsweise in Fortran, Perl oder Python). Aufgrund der verschiedenen Wahlen für die Definitionsbereiche von Basis und Exponent stellt Haskell gleich drei Potenzoperatoren zur Verfügung: a^b, a^^b und a**b.

Zehnerpotenzen werden in der elektronischen Datenverarbeitung oder in der Anzeige auf Taschenrechnern häufig mit e oder E dargestellt.
Häufig anzutreffende Darstellung für z.B. −299792458 = −2,99792458·10⁸

`-2.9979 08`	(8-stellige 7-Segment-Anzeige)
`-2.997925 08`	(10-stellige 7-Segment-Anzeige)
`-2.9979256 ⁰⁸`	(8-stellige 7-Segment-Anzeige + Exponentenfeld)
`-2.99792458 E+08`	(16-stellige Punktmatrixanzeige)
`-2.99792458E+08`	(Gleitkommadarstellung nach IEEE)

Potenzgesetze

Um die nachfolgende Tabelle nicht zu überladen, betrachten wir nur Potenzen mit reellen Basen, die ungleich $0$ sind. Betrachtet man aber eines der unten aufgeführten Gesetze mit nur positiven Exponenten, dann ist es auch für Potenzen zur Basis $0$ gültig. Wenn von rationalen Zahlen mit geraden oder ungeraden Nennern gesprochen wird, dann sind stets die Nenner ihrer gekürzten Bruchdarstellungen gemeint.

	für alle $a\ne 0$ (Anmerkungen zu „null hoch null“ siehe unten)
$a^{{-r}}={\frac {1}{a^{r}}}$	für beliebige reelle , falls ist; für beliebige rationale mit ungeraden Nennern, falls ist.
$a^{{{\frac {m}{n}}}}={\sqrt[ {n}]{a^{m}}}=({\sqrt[ {n}]a})^{m}$	für beliebige natürliche und ganze , falls ist; für beliebige natürliche ungerade und ganze , falls ist.
$a^{{r+s}}=a^{r}\cdot a^{s}$	für beliebige reelle , falls ist; für beliebige rationale mit ungeraden Nennern, falls ist.
$a^{{r-s}}={\frac {a^{r}}{a^{s}}}$	für beliebige reelle , falls ist; für beliebige rationale mit ungeraden Nennern, falls ist.
$(a\cdot b)^{r}=a^{r}\cdot b^{r}$	für beliebige natürliche , und für ganze , wenn $a\cdot b\neq 0$ ; für beliebige reelle , falls $a>0,b>0$ sind; für beliebige rationale mit ungeraden Nennern, falls mindestens eine der Zahlen negativ ist.
$\left({\frac {a}{b}}\right)^{r}={\frac {a^{r}}{b^{r}}}$	für beliebige $b\neq 0$ und ganze und, wenn $r\leq 0$ , auch $a\neq 0$ ; für beliebige reelle , falls $a>0,b>0$ sind; für beliebige rationale mit ungeraden Nennern, falls mindestens eine der Zahlen negativ ist.
$(a^{r})^{s}=a^{{r\cdot s}}$	für beliebige ganze , falls $a\ne 0$ ist; für beliebige reelle , falls ist; für beliebige rationale $r,s$ , mit ungeraden Nennern, falls ist.

Ist mindestens einer der Exponenten r, s irrational oder sind beide rational, aber hat mindestens eine der Zahlen oder $r\cdot s$ einen geraden Nenner, dann ist einer der Ausdrücke $(a^{r})^{s}$ oder $a^{{r\cdot s}}$ für a<0 undefiniert. Ansonsten sind beide definiert und stimmen entweder überein oder unterscheiden sich nur um ihr Vorzeichen. Für beliebige r, s , falls a>0 ist, und für ganze r, s , falls $a\ne 0$ ist, stimmen sie immer überein. Für a<0 und nicht ganzzahlige, aber rationale r, s sind diese beiden Fälle möglich. Welcher Fall eintritt, hängt von der Anzahl der Zweien in der Primzahlzerlegung des Zählers von und des Nenners von ab. Um das richtige Vorzeichen auf der rechten Seite der Formel $(a^{r})^{s}=\pm a^{r\cdot s}$ zu erkennen, ist es hinreichend, in diese Formel a = -1 einzusetzen. Das Vorzeichen, mit dem sie dann bei a = -1 gültig ist, bleibt richtig für alle a<0 und gegebenem r, s . Gilt $(a^{r})^{s}=-a^{{r\cdot s}}$ für a<0 , dann gilt $(a^{r})^{s}=|a|^{{r\cdot s}}$ für alle $a\neq 0$ (und auch für a=0 , falls alle Exponenten positiv sind).

Zum Beispiel gilt $((-1)^{2})^{{{\frac {1}{2}}}}=1$ und $(-1)^{{2\cdot {{\frac {1}{2}}}}}=-1$ . Darum ist ${\sqrt {a^{2}}}=(a^{2})^{{{\frac {1}{2}}}}=-a^{{2\cdot {{\frac {1}{2}}}}}=-a$ für alle a<0 und somit ${\sqrt {a^{2}}}=|a|$ für alle reellen gültig.

Das Potenzieren ist weder kommutativ, denn beispielsweise gilt $2^{3}=8\not =9=3^{2}$ , noch assoziativ, denn beispielsweise gilt $\left(3^{1}\right)^{3}=27\neq 3=3^{{\left(1^{3}\right)}}$ .

Die Schreibweise $a^{{b^{c}}}$ ohne Klammern bedeutet $a^{{(b^{c})}}$ >, das Potenzieren ist demnach rechtsassoziativ, vgl. Operatorrangfolge.

Potenzen komplexer Zahlen

Für ganzzahlige Exponenten kann man Potenzen mit komplexen Basen wie im reellen Fall definieren. Für beliebige reelle oder komplexe Exponenten muss man jedoch anders vorgehen.

Der erste Schritt zur Definition von Potenzen mit komplexen Basen und Exponenten besteht in der stetigen Fortsetzung der Funktion $e^{x}$ auf die Menge $\mathbb {C}$ der komplexen Zahlen. Dafür gibt es unterschiedliche Möglichkeiten. Zum Beispiel kann man die Reihe

$e^{z}=\sum _{{n=0}}^{{\infty }}{{\frac {z^{n}}{n!}}}$

benutzen, die für alle $z\in {\mathbb C}$ konvergiert und für alle $z=x\in {\mathbb R}$ die Funktion $e^{x}$ angibt. Mithilfe von Operationen mit Reihen beweist man danach, dass

$e^{{z_{1}+z_{2}}}=e^{{z_{1}}}e^{{z_{2}}}$

für beliebige $z_{1},z_{2}\in {\mathbb C}$ und die eulersche Formel

$e^{i\,y}=\cos y+i\,\sin y$

für beliebige $y\in {\mathbb R}$ gelten. Daraus folgt die Formel

$e^{x+i\,y}=e^{x}\,(\cos {y}+i\,\sin {y})$ ,

die man auch für die Definition von $e^{z}$ benutzen kann. Diese Formel zeigt, dass die Wertemenge von $e^{z}$ gleich ${\mathbb C}\setminus \{0\}$ ist und dass diese Funktion periodisch ist mit Perioden $2k\pi i$ , $k\in {\mathbb Z}$ .

Darum ist ihre Umkehrfunktion $\operatorname {Ln} (z)$ mehrdeutig und für alle $z\neq 0$ definiert. Sie kann mithilfe der Formel $\operatorname {Ln} (z)=\ln |z|+i\operatorname {Arg} (z)$ angegeben werden, wobei |z| der Betrag, $\operatorname {Arg} (z)$ die Wertemenge des Arguments von und $\ln |z|$ der übliche reelle Logarithmus ist. Der Hauptwert $\ln(z)$ dieser Funktion ergibt sich, wenn man den Hauptwert $\operatorname {arg} (z)$ anstatt $\operatorname {Arg}(z)$ benutzt. Für reelle z=x>0 ist nach der üblichen Definition $\operatorname {arg} (x)=0$ , deshalb stimmt diese Funktion $\ln$ auf der Menge ${\mathbb R}^{+}$ mit dem üblichen reellen Logarithmus überein.

Für beliebige $a,z\in \mathbb {C}$ mit $a\ne 0$ definiert man dann:

$a^{z}=e^{z\,\operatorname {Ln} \,a}$

Das ist auch eine mehrdeutige Funktion, deren Hauptwert sich beim Einsatz von $\ln$ anstatt $\operatorname {Ln}$ ergibt.

Aber für $z=n\in {\mathbb Z}$ verschwindet diese Mehrdeutigkeit und es entstehen übliche Potenzen mit ganzen Exponenten, die im ersten Abschnitt definiert wurden. Seien $a\ne 0$ und $\varphi \in \operatorname {Arg} (a)$ , dann zieht die exponentielle Darstellung

$a=|a|\,e^{i\varphi }$

nach sich, dass

$a^{n}=|a|^{n}\,e^{in\varphi }$

gilt.

Für einen rationalen Exponenten mit der gekürzten Bruchdarstellung $q={\tfrac mn}$ , mit $m\in {\mathbb Z},n\in {\mathbb N}$ , hat die Potenz $a^{q}$ genau unterschiedliche Werte. Dies gilt insbesondere für ${\sqrt[ {n}]a}=a^{{{\frac 1n}}}$ . Ist ungerade und $a\in {\mathbb R}$ , dann gibt es unter ihnen genau eine reelle Zahl, und das ist gerade die Zahl $a^{q}$ aus dem Abschnitt 1.3. Ist gerade und a<0 , dann nimmt $a^{q}$ keine reellen Werte an. Wenn aber gerade und a>0 ist, dann nimmt die Potenz $a^{q}$ genau zwei reelle Werte an, die unterschiedliche Vorzeichen haben. Der positive davon ist in diesem Fall gerade gleich der Zahl $a^{q}$ aus dem Abschnitt 1.3.

Als ein Beispiel betrachten wir die Potenz hoch .

Aus |i|=1 und

$\operatorname {Arg} (i)={\frac {\pi }{2}}+2{\pi }k$ mit $k\in {\mathbb Z}$

folgt

$\operatorname {Ln} (i)=i\left({\frac {\pi }{2}}+2{\pi }k\right).$

Daraus ergibt sich

$i^{i}=e^{{i\cdot i({{\frac {\pi }2}}+2\pi k)}}=e^{{-{{\frac {\pi }2}}-2\pi k}}$ mit $k\in {\mathbb Z}$

Der Hauptwert entspricht k=0 und ist gleich $e^{{-{{\frac {\pi }2}}}}.$

Spezielle Potenzen

Ganzzahlige Potenzen von 10 (Zehnerpotenzen) bilden die Grundlage unseres Zahlensystems, des Dezimalsystems. Als Potenz geschrieben, z.B. 10⁻⁹ für 0,000000001 oder 10¹¹ für 100 Milliarden, werden sie in den Naturwissenschaften zur Darstellung sehr großer oder sehr kleiner positiver Zahlen verwendet.

In der Mathematik und Technik besonders wichtig sind weiterhin Potenzen mit der Basis $e\approx 2{,}7182818284590452$ , der Eulerschen Zahl.

Zweierpotenzen ergeben sich durch wiederholte Verdoppelung. Das überraschend schnelle Anwachsen der Zahlen macht Zweierpotenzen für Praxisbeispiele beliebt:

Ein Blatt Papier üblicher Größe lässt sich nur etwa siebenmal auf die halbe Größe falten. Es hat dann 128 Lagen und nur noch ein 128-tel seiner Fläche. Wenn man es 42-mal falten könnte, was nur theoretisch geht, entspräche seine Dicke von ca. 400.000 km etwa der Entfernung von der Erde zum Mond.
Jeder Mensch hat zwei biologische Eltern und die meisten haben vier Großeltern und acht Urgroßeltern. Ohne Ahnenverlust wären das vor 70 Generationen, zur Zeit Christi Geburt, $2^{{70}}\approx 10^{{21}}$ Ahnen, obwohl damals weniger als 10⁹ Menschen gelebt haben.
Die Weizenkornlegende vom Erfinder des Schachspiels, der auf jedem Feld des Schachbrettes die Anzahl der Weizenkörner verdoppelte, verdeutlicht ebenfalls das rasante Wachstum der Zweierpotenzen.

Zur digitalen Verarbeitung von Daten am Computer wird das Dualsystem mit der Basis 2 verwendet. Die Größeneinheiten digitaler Speichersysteme sind daher die Zweierpotenzen, also die Potenzen zur Basis 2 (das sind 1, 2, 4, 8, 16, …). Ein Kibibyte (abgekürzt KiB) entspricht $2^{{10}}=1024$ Bytes.

Bei Schneeballsystemen, zum Beispiel sogenannten Schenkkreisen, werden zum Teil Systeme gestartet, die nicht nur eine Verdoppelung, sondern zum Beispiel eine Verachtfachung der neuen Mitglieder pro Schritt vorsehen. Solche Folgen wachsen derart schnell an, dass die Systeme bereits nach wenigen Schritten zwangsläufig kollabieren. Eine oft von den Initiatoren suggerierte Stabilität der Schneeballsysteme kann nicht bestehen. Sie sind daher aus gutem Grunde in vielen Ländern verboten.

Null hoch Null

Analysis

Der Graph der Funktion $z=x^{y}$ für $x\in [0,1]$ und $y\in [-1,+1]$ unter besonderem Augenmerk auf die Umgebung von $(0;0;z)$ , in welcher (senkrechten) Geraden die Fläche endet. Die farbigen Kurven zeigen verschiedene Annäherungen an (0;0) mit verschiedenen Grenzwerten für .

Die Frage, ob und auf welche Weise dem Ausdruck 0^0 ein eindeutiger Wert zugeordnet werden kann, hat die Mathematiker spätestens seit der ersten Hälfte des 19. Jahrhunderts beschäftigt.

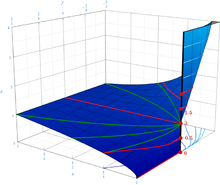
Die nebenstehende Abbildung veranschaulicht in ihrer 3D-Darstellung des Graphen der Funktion $z=x^{y}$ , dass beliebige Werte $z\in \mathbb {R} _{\geq 0}$ durch geeignete Wahl von Näherungspunkten $(x;y)$ an den Ursprung (0;0) erreicht werden können. So ist z.B.

$\lim _{y\to 0+}0^{y}=0$ ,
$\lim _{y\to 0+}{\Bigl (}e^{-y^{-2}}{\Bigr )}^{y}=0$ ,
$\lim _{t\to +\infty }x^{y}=c$
mit , $x=c^{t}$ und $y={\tfrac {1}{t}}$ ,
$\lim _{x\to 0+}x^{0}=1$ und
$\lim _{y\to 0-}{\Bigl (}e^{-y^{-2}}{\Bigr )}^{y}=+\infty$ .

Die Beispiele zeigen, dass die Funktion $z=x^{y}$ an der Stelle (0;0) divergiert, denn ein Grenzwert von der Art $\textstyle \lim _{(x;y)\to (0;0)}\;x^{y}$ existiert offensichtlich nicht.

Ein Ausdruck, der unter dem Zeichen des Grenzwertes steht und der sich nicht auf Grund von Grenzwertsätzen und Stetigkeitseigenschaften berechnen lässt, heißt unbestimmter Ausdruck. Beispiele sind ${\tfrac {0}{0}},\,{\tfrac {\infty }{\infty }}$ sowie 0^0 . Letzterer Ausdruck entsteht bei Berechnungen von Potenzen, deren Basis und Exponent gleichzeitig gegen $0$ geht, und kann nicht bestimmt werden, wenn es keine Beziehung zwischen den beiden gibt.

Als einen unter naheliegenden Umständen geeigneten Wert kann man (das ist in der Abbildung die Gerade $(x;0;1)$ , weil $x^{0}=1$ für beliebige $x\in \mathbb {R} ^{\times }$ gilt) oder $0$ (der Strahl $(0;+y;0)$ , weil $0^{y}=0$ für $y\in \mathbb {R} ^{+}$ gilt) ansehen. Es gibt aber auch moderne Analysislehrbücher, die die Potenz 0^0 (in dieser Form) ausdrücklich undefiniert lassen.

Bis Anfang des 19. Jahrhunderts haben Mathematiker anscheinend $0^{0}=1$ gesetzt, ohne diese Festlegung genauer zu hinterfragen. Augustin-Louis Cauchy listete allerdings 0^0 gemeinsam mit anderen Ausdrücken wie 0/0 in einer Tabelle von unbestimmten Ausdrücken. 1833 veröffentlichte Guillaume Libri eine Arbeit, in der er wenig überzeugende Argumente für $0^{0}=1$ präsentierte, die in der Folge kontrovers diskutiert wurden. Zur Verteidigung von Libri veröffentlichte August Ferdinand Möbius einen Beweis seines Lehrers Johann Friedrich Pfaff, der im Wesentlichen zeigte, dass $\textstyle \lim _{x\to 0+}x^{x}=1$ gilt, und einen angeblichen Beweis für $\textstyle \lim _{t\to 0+}x(t)^{y(t)}=1$ , falls $\textstyle \lim _{t\to 0+}x(t)=\lim _{t\to 0+}y(t)=0$ > gelten, lieferte. Die Korrektheit dieses Beweises wurde durch das Gegenbeispiel $x(t)=e^{-1/t}$ und $y(t)=t$ rasch widerlegt.

Donald E. Knuth erwähnte 1992 im American Mathematical Monthly die Geschichte der Kontroverse und lehnte die Schlussfolgerung entschieden ab, dass 0^0 undefiniert gelassen wird. Wenn man den Wert 1 für die Potenz 0^0 nicht voraussetzt, verlangen viele mathematische Aussagen wie zum Beispiel der binomische Satz

$(a+b)^{n}=\sum _{k=0}^{n}{n \choose k}a^{k}b^{n-k}$

eine Sonderbehandlung^[1] für die Fälle a=0 (am Index k=0 ) oder b=0 (am Index k=n ) oder a+b=0 (bei n=0 ).

Ebenso kommt die Potenz 0^0 in Potenzreihen wie beispielsweise für die Exponentialfunktion

$e^{t}=\sum _{n=0}^{\infty }{\frac {t^{n}}{n!}}$

für t=0 am Index n=0 oder in der Summenformel für die geometrische Reihe

$\sum _{{k=0}}^{n}q^{k}={\frac {1-q^{{n+1}}}{1-q}}$

für q=0 am Index k=0 vor. Auch hier hilft die Konvention $0^{0}=1$ .

Die angeführten Anwendungsfälle der Potenz 0^0 sind (wie außerordentlich viele ähnliche andere) Aussagen über Polynome, Multinome oder Potenzreihen, bei denen der Exponent des Terms $x^{y}$ konstant 0 ist und die Basis – eher ausnahmsweise – den Wert 0 annehmen kann. In allen diesen Fällen sind die vorkommenden Terme stetige Summanden oder Faktoren, die für invertierbares den Wert 1 haben, deren Wert dann auch für die Lücke $x\to 0$ mühelos (und ganz im Sinn von 0^0 = 1 ) als 1 stetig ergänzt werden kann.

Knuth differenziert jedoch und schreibt: “Cauchy had good reason to consider 0^0 as an undefined limiting form” (deutsch etwa: Cauchy hatte guten Grund, 0^0 als unbestimmten Limes-Ausdruck zu betrachten), wobei er unter der limiting form 0^0 Grenzprozesse der Form $\lim x(t)^{y(t)}$ versteht, bei denen sich sowohl die Basis x(t) wie der Exponent y(t) für ein gewisses der 0 beliebig nähern.

Mit dieser Maßgabe von D. E. Knuth sind die einfachen Fälle der Absolutglieder in Polynomen und Potenzreihen unmittelbar und pauschal gelöst, ohne dass es zu einem Konflikt mit einer detaillierten Betrachtung komplizierterer Grenzprozesse käme.

Mengenlehre

In der Mengenlehre wird eine Potenz $B^{A}$ zweier Mengen als Menge aller Funktionen von nach definiert, das heißt als Menge von Mengen geordneter Paare (a,b) , sodass es zu jedem $a\in A$ genau ein $b\in B$ gibt mit $(a,b)\in f$ . Bezeichnet man mit |A| die Mächtigkeit von , so gilt $|B^{A}|=|B|^{{|A|}}$ (für endliche Mengen, aber auch darüber hinaus), was die Potenzschreibweise für Mengen rechtfertigt. Nun gibt es genau eine auf der leeren Menge $\emptyset$ definierte Funktion, das heißt Menge von Paaren mit obiger Eigenschaft, nämlich $\emptyset$ . Daher gilt $B^{\emptyset }=\{\emptyset \}$ , was auch für $B=\emptyset$ richtig bleibt.

Die natürlichen Zahlen werden in der Mengenlehre rekursiv wie folgt definiert (siehe von Neumanns Modell der natürlichen Zahlen):

$0:=\emptyset ,\,1:=\{0\}=\{\emptyset \},\,2:=\{0,1\}=\{\emptyset ,\{\emptyset \}\},\,3:=\{0,1,2\}=\dotsb$

Demnach gilt in der Mengenlehre:

$0^{0}=\emptyset ^{\emptyset }=\{\emptyset \}=1$

Umkehrfunktionen

Da das Kommutativgesetz beim Potenzieren nicht gilt, gibt es zwei Umkehrrechenarten:

das Wurzelziehen, um Gleichungen der Bauart $x^{a}=b$ nach aufzulösen, also um die Basis zu ermitteln, wenn der Exponent bekannt ist,
das Logarithmieren für Gleichungen des Typs $a^{x}=b$ , also die Bestimmung des Exponenten, wenn die Basis gegeben ist.

Verallgemeinerungen

>Allgemeinere Basen

Allgemein gibt es Potenzen mit positiven, ganzzahligen Exponenten in jeder Halbgruppe. Hat diese ein neutrales Element und wird dadurch zum Monoid , so ist auch Exponent 0 sinnvoll, $a^{0}$ ist dann immer das neutrale Element. Es gelten für alle $a,b\in M;m,n\in \mathbb{N} _{0}$ die Potenzgesetze

$a^{{m+n}}=a^{m}\cdot a^{n}$
$(a^{m})^{n}=a^{{m\cdot n}}$
$(a\cdot b)^{m}=a^{m}\cdot b^{m}$ , falls und vertauschen, d.h. wenn gilt.

Ist ein invertierbares Element, so kann man mittels

$\!\ a^{{-n}}=(a^{{-1}})^{n}$ für $n\in \mathbb {N}$

Potenzen mit beliebigen ganzzahligen Exponenten definieren. Die Rechenregeln gelten analog. Im Fall abelscher Gruppen besagen sie, dass durch die Potenzierung die Struktur eines $\mathbb {Z}$ -Moduls induziert wird.

Allgemeinere Exponenten

Allgemeinere Exponenten wie Matrizen werden meist nur im Zusammenhang mit der Basis , also als Werte der verallgemeinerten Exponentialfunktion betrachtet.

Darüber hinaus wird die Potenzschreibweise gelegentlich auch für andere natürliche Fortsetzungen verwendet. So werden beispielsweise in der algebraischen Zahlentheorie gelegentlich Potenzen von Elementen von (topologischen) Galoisgruppen mit Exponenten in Vervollständigungen von $\mathbb {Z}$ betrachtet; es handelt sich dann um die jeweils eindeutig bestimmte stetige Fortsetzung der Abbildung

${\mathbb Z}\to G,\quad n\mapsto g^{n}.$

Für beliebige Kardinalzahlen |X| und |Y| lässt sich die Potenz durch $|Y|^{{|X|}}:=|Y^{X}|$ definieren, wobei Y^X die Menge aller Funktionen mit Urmenge und Bildmenge bezeichnet, diese Verallgemeinerung setzt das Potenzmengenaxiom voraus, wobei zur Handhabung der Kardinalzahlen in der Regel auch das Auswahlaxiom angenommen wird.

Mehrdeutigkeit der Exponentenschreibweise

Die Exponentenschreibweise kann insbesondere bei Funktionen verschiedene Bedeutungen haben, je nachdem, ob die Schreibweise die Iteration der Verkettung oder der punktweisen Multiplikation wiedergeben soll. Darüber hinaus könnte auch ein oberer Index gemeint sein. In der Regel geht aus dem Kontext hervor, was gerade gemeint ist.

Verkettung

Die Potenzschreibweise wird oft als abkürzende Schreibweise für die Verkettung von Funktionen, deren Werte wieder im Definitionsbereich liegen, verwendet, zum Beispiel für Iterationen in dynamischen Systemen.

Man definiert, wobei id die Identität auf dem Definitionsbereich bezeichnet, rekursiv:

$f^{0}:={\mathrm {id}};\quad f^{n}:=f\circ f^{{n-1}}$

für $n\geq 1$ , also

$f^{1}:=f;\quad f^{2}:=f\circ f,$

und so weiter.

Für die Funktionswerte bedeutet dies

$f^{0}(x)={\mathrm {id}}(x)=x;\quad f^{1}(x)=f(x);\quad f^{2}(x)=(f\circ f)(x)=f(f(x))$

und allgemein

$f^{n}(x)=(f\circ f^{{n-1}})(x)=f\left(f^{{n-1}}(x)\right).$

Als Erweiterung dieser Definition definiert man üblicherweise noch $f^{-1}$ als die Umkehrfunktion von . Insbesondere findet sich diese Schreibweise auch auf vielen Taschenrechnern, beispielsweise wird dort und auch sonst die Arkusfunktion $\arcsin$ mit $\sin^{-1}$ bezeichnet. Oft bezeichnet $f^{-1}$ auch die Urbildfunktion.

Multiplikation

Als abkürzende Schreibweise für die Multiplikation mehrerer Funktionswerte trigonometrischer Funktionen mit gleichen Argumenten, wie sie beispielsweise bei den Additionstheoremen für Winkelfunktionen häufig auftreten, hat sich ebenfalls die Potenzschreibweise eingebürgert, das heißt, man schreibt

$\sin ^{2}\!x:=(\sin x)^{2}=\sin(x)\cdot \sin(x)=\sin x\cdot \sin x$ .

Dies ist nicht mit der oben vorgestellten Schreibweise für die Verkettung von Funktionen verträglich. Gleiches gilt für Polynome. Mit $x^{n}$ meint man immer das -fache Produkt der Unbestimmten mit sich selbst. Da die Unbestimmte als Polynomfunktion die identische Abbildung ist, wäre die Potenzschreibweise als Iteration von Funktionen hier nicht sinnvoll.

Oberer Index

Für indizierte Größen schreibt man den Index manchmal hochgestellt, sodass in den Formeln der Eindruck einer Potenzierung entstehen könnte. Das kommt besonders in der Tensorrechnung vor, etwa bei der Bezeichnung von Vektorfeldern in Koordinatenschreibweise, oder bei der Indizierung von Größen, die ihrerseits bereits indiziert sind, etwa Folgen von Folgen.

Ableitung

Wird der Exponent in Klammern geschrieben, so ist meist die entsprechende Ableitung gemeint, $f^{(n)}$ bezeichnet dann die -te Ableitung der Funktion .

Anmerkungen

↑ Man kann es − mit letztlich demselben Ergebnis − auch andersherum sehen: Die Schreibweise $\textstyle \sum _{k=0}^{n}{n \choose k}a^{k}b^{n-k}$ ist eine „Kurzform“ von $\textstyle a^{n}+\sum _{k=1}^{n-1}{n \choose k}a^{k}b^{n-k}+b^{n}$ , die keinen Exponenten 0 enthält. Dabei ist vereinbart, dass der Wert einer Potenz als 1 zu nehmen ist, wenn ihr Exponent durch eine Konstellation der Laufvariablen 0 wird.