Geometrische Reihe
Eine geometrische Reihe ist eine spezielle mathematische
Reihe.
Eine geometrische Reihe ist die Reihe einer geometrischen Folge.
Bei einer geometrischen Folge ist der Quotient
zweier benachbarter Folgenglieder
konstant. Für
gilt
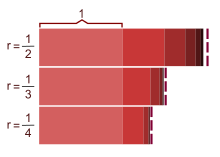
Ein Startwert der geometrischen Folge von 1 und ein Quotient größer als 1 (hier 2) ergibt eine divergierende geometrische Reihe: 1, 1 + 2, 1 + 2 + 4, 1 + 2 + 4 + 8, …, zusammengefasst also 1, 3, 7, 15, …
Bei identischem Startwert und einem Quotienten von 1/2 ergibt sich hingegen
die geometrische Reihe: 1, 1 + 1/2, 1 + 1/2 + 1/4, 1 + 1/2 + 1/4 + 1/8, …, also
1, 3/2, 7/4, 15/8, … mit dem Grenzwert .
Berechnung der (endlichen) Partialsummen einer geometrischen Reihe
Eine Reihe ist per Definition eine Folge von Partialsummen. Der Wert der
Reihe ist der Grenzwert dieser Folge von Partialsummen. Eine endliche Summe ist
somit ein Folgenglied aus der Folge der Partialsummen. Die (endliche) Summe der
ersten
Glieder einer Reihe bezeichnet man also als
-te
Partialsumme und nicht etwa als „Partialreihe“ o. ä.
Gegeben sei eine geometrische
Folge .
ist die zugehörige geometrische Reihe.
Wir können daraus eine neue Folge
konstruieren, deren -tes
Glied jeweils die Summe der ersten
Glieder der Reihe
ist, die sogenannte
-te
Partialsumme
von
.
Diese Folge heißt die Folge der Partialsummen zu
.
(Genau genommen wird in umgekehrter Reihenfolge die Reihe auf Grundlage von
Partialsummen einer Folge definiert. Die obige und übliche Schreibweise für die
Reihe gibt das aber nicht her, deshalb müssen wir aus ihr erst die Folge der
Partialsummen rekonstruieren.) Falls sie konvergiert, wird über sie der
Wert der Reihe
definiert. Es gilt für den Wert der Reihe s (hier wird nicht mehr von
„Grenzwert“ gesprochen):
in Worten: Der Wert der Reihe
ist definiert als der Grenzwert der zu ihr gehörigen Partialsummen-Folge, falls
diese konvergiert, andernfalls wird die Reihe als divergent
bezeichnet. Falls in diesem Falle die Folge der Partialsummen gegen (plus /
minus) Unendlich strebt, schreibt man gewöhnlich
oder
und sagt, die Folge konvergiere gegen den uneigentlichen
Grenzwert (plus / minus) Unendlich oder die Reihe habe den
uneigentlichen Wert (plus / minus) Unendlich. (Eine
Berechnungsformel für den Grenzwert folgt weiter unten.)
Mit
bezeichnen wir nun das Verhältnis
zweier benachbarter Glieder, das für alle
gleich ist.
Dann gilt
für alle
.
Für die -te
Partialsumme
ergibt sich damit:
Wenn ,
dann gilt (Herleitung
siehe unten)
Falls ,
so gilt
Das Obige gilt, wenn die Folgenglieder Elemente eines unitären Ringes sind, also insbesondere, wenn es reelle Zahlen sind.
Verwandte Summenformel 1
Die Partialsumme
hat für
das Ergebnis
und für
(vgl. Gaußsche
Summenformel)
;
diese Formel ergibt sich auch aus der Formel für
(mit zweifacher Anwendung der Regel
von de l’Hospital) als deren Grenzwert
für
.
Verwandte Summenformel 2
Die Partialsumme
hat für
das Ergebnis
und für
(vgl. Potenzsummen)
Beispiele
Zahlenbeispiel
Gegeben sei die geometrische Folge
mit
und
Die zugehörige geometrische Reihe ist
Die zugehörige Folge von Partialsummen ergibt sich zu
usw.
Rentenrechnung
Angenommen, man zahlt am Anfang eines jeden Jahres 2000 € bei einer Bank ein
und die Zinsen liegen bei 5 % [d. h. der Zinsfaktor
ist: ].
Wie viel Geld hat man am Ende des fünften Jahres?
Das im ersten Jahr eingezahlte Geld wird fünf Jahre lang verzinst, man erhält dafür am Ende inklusive Zinseszins 2000 · 1,055 €. Das im zweiten Jahr eingezahlte Geld wird nur noch vier Jahre verzinst und so weiter. Insgesamt ergibt sich dann durch die Rentenrechnung ein angesparter Betrag von
Durch Zinsen hat sich das Kapital somit um 1603,83 € erhöht. Beim Nachrechnen von Kontoauszügen ist zu bedenken, dass im Bankenwesen nicht mathematisch gerundet wird.
Zum Vergleich: Würden nicht Jahr für Jahr je 2000 € eingezahlt, sondern gleich von Beginn an die ganzen 10000 € über 5 Jahre bei 5 % Zinsen angelegt, so wäre der Endbetrag
also ein Kapitalertrag von 2762,82 €.
Allgemein gilt: Beträgt die Einlage am Anfang jedes Jahres ,
der Zinsfaktor
und die Laufzeit
Jahre, dann ist der Endwert
.
Rentenrechnung mit linearer Dynamik
Zahlt man im Gegensatz zum vorigen Beispiel nicht jährlich einen festen
Beitrag ,
sondern ab dem 2. Jahr jedes Jahr
mehr als im Vorjahr (lineare
Dynamik)
ein, so ist der Endwert
zum Beispiel mit €
im ersten Jahr, jedes Jahr
€
mehr als im Vorjahr, 5 % Zinsen (also Zinsfaktor
)
und
Jahren Laufzeit, dann ist der am Ende des 5. Jahres angesparte Betrag
wobei in diesem Beispiel nicht 10.000 €, sondern insgesamt 11.000 €
eingezahlt wurden, also beträgt der Gewinn 1.707,65 €. Zahlt man statt
€
im ersten Jahr nur
€
ein und lässt die anderen Faktoren gleich (sodass man wie im vorletzten Beispiel
insgesamt 10.000 € einzahlt), dann ist der Endwert nur noch
11.547,27 €, das heißt zahlt man den gleichen Betrag ein, nur zu Beginn
weniger, dafür später mehr, dann entgehen einem Gewinne (Opportunitätskosten).
Periodische Dezimalbrüche
Periodische Dezimalbruchentwicklungen enthalten eine geometrische Reihe, welche mit den obigen Formeln wieder in einen Bruch umgewandelt werden kann.
Beispiel 1:
Beispiel 2:
Konvergenz und Wert der geometrischen Reihe
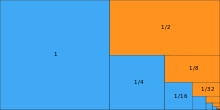
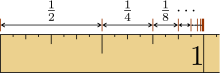
Eine geometrische Reihe bzw. die Folge ihrer Partialsummen konvergiert genau
dann, wenn der Betrag der reellen
(oder komplexen)
Zahl
kleiner als Eins oder ihr Anfangsglied
gleich Null ist. Für
oder
konvergiert die zugrundeliegende geometrische Folge nämlich gegen Null:
.
Nach dem Nullfolgenkriterium
ist dies eine notwendige
Bedingung für die Konvergenz der geometrischen Reihe. Da für
und
die Grundfolge divergiert, liegt in diesem Falle somit auch Divergenz der Reihe
vor.
Für
ergibt sich die Divergenz der geometrischen Reihe aus
,
ein Ausdruck, der für
und
divergiert.
Für den Fall
ergibt sich die Divergenz immer als bestimmte Divergenz (s.o.), für den Fall
immer als unbestimmte
Divergenz. Die geometrische Reihe konvergiert auch
absolut, sofern sie auf normale Weise konvergiert.
Der Wert der Reihe im Konvergenzfall ergibt sich aus jener obenstehenden
Formel für die -ten
Partialsummen durch Grenzwertbildung (
)
für
zu
denn es ist
Die letzte Formel ist sogar in jeder Banach-Algebra gültig,
solange die Norm von
kleiner als Eins ist; im Kontext linearer
Operatoren spricht man auch von der Neumann-Reihe.
Herleitungen
Herleitung der Formel für die Partialsummen
Die -te
Partialsumme
der geometrischen Reihe lässt sich wie folgt berechnen:
Vereinfacht:
(Gleichung 1)
Durch Multiplikation mit
ergibt sich:
(Gleichung 2)
Wenn man Gleichung 2 von Gleichung 1 subtrahiert, erhält man:
Ausklammern von :
Teilen durch
liefert für
die gesuchte Formel für die Partialsummen:
Herleitung der Varianten
Mithilfe der oben angegebenen Formel lassen sich durch gliedweise
Differentiation auch folgende endliche Reihen geschlossen darstellen, für
Für
konvergieren nach Grenzwertbildung der zugehörigen endlichen Reihe auch die
unendlichen Reihen (folglich sind diese sogar gliedweise integrierbar):
analog für höhere Potenzen.
Siehe auch
- Die Konvergenz bzw. Divergenz der geometrischen Reihe ist die Grundlage für das Wurzelkriterium und das Quotientenkriterium.
- Geometrische Verteilung
- Arithmetische Reihe
- Harmonische Reihe


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 25.03. 2021