Reihe (Mathematik)
Eine Reihe, selten Summenfolge
und vor allem in älteren Darstellungen auch unendliche Reihe genannt,
ist ein Objekt aus dem mathematischen
Teilgebiet der Analysis.
Anschaulich ist eine Reihe eine Summe
mit unendlich vielen Summanden. Präzise wird eine
Reihe als eine Folge
definiert, deren Glieder die Partialsummen einer anderen Folge sind. Wenn
man die Zahl 0 zur Indexmenge
zählt, ist die -te
Partialsumme die Summe der ersten
(von den unendlich vielen) Summanden. Falls die Folge dieser Partialsummen einen
Grenzwert
besitzt, so wird dieser der Wert oder die Summe der Reihe genannt.
Definition
Ist eine beliebige Folge
gegeben, kann man aus ihr eine neue Folge
der Partialsummen bilden. Die
-te
Partialsumme ist die Summe der ersten
Glieder von
,
ihre Definition lautet:
Die Folge
der
-ten
Partialsummen heißt Reihe. Falls die Reihe (also die Folge der
Partialsummen) konvergiert,
so nennt man ihren Grenzwert
Wert der Reihe oder Summe der Reihe.
Notation
Für Reihen gibt es je nach Kontext unterschiedliche Notationen. In diesem Artikel werden als Indizes für die Glieder von Folge und Reihe die natürlichen Zahlen einschließlich der Null verwendet. Bei manchen Anwendungen ist es zweckmäßig, die Summation erst beim Index 1, 2 oder höher zu beginnen, selten kommen auch negative Indizes vor (siehe Laurent-Reihe). Mit Hilfe des Summenzeichens können die einzelnen Glieder der Reihe auch abgekürzt als
geschrieben werden. Ebenso geht man bei der Folge der Einzelglieder vor und schreibt kurz
Häufig werden ein Teil oder alle Indizes weggelassen, wenn Missverständnisse ausgeschlossen sind. Ist etwa wie hier im Kontext von Berechnungen mit unendlichen Reihen klar, dass generell bei 0 zu nummerieren angefangen wird, so steht
für
Auswertung und Einteilung
Wenn
und damit auch
für alle nichtnegativen ganzen Indizes i bzw. n definiert sind,
lässt sich somit eine unendliche Reihe bilden: wenn der Grenzwert der Folge
der Partialsummen
existiert, sagt man, die Reihe konvergiert; den Grenzwert S nennt man die Summe der Reihe oder den Wert der Reihe. Mit Hilfe des Summenzeichens kann diese Summe auch abgekürzt als
geschrieben werden.
Eine Reihe
heißt divergent oder ihr Grenzwert nicht existent, wenn die Reihe nicht
konvergiert. Sie heißt bestimmt
divergent oder uneigentlich
konvergent, wenn die Teilsummen
gegen −∞ oder +∞ streben. Andernfalls heißt die Reihe unbestimmt
divergent; dabei kann sie Häufungspunkte
haben oder auch nicht.
Mit verschiedenen Konvergenzkriterien lässt sich feststellen, ob eine Reihe konvergiert.
Beispiele
Eine klassische Reihe ist die geometrische
Reihe, der Name ergibt sich aus der geometrischen
Folge (
für
).
Die geometrische Reihe ist also:
Eine spezielle geometrische Reihe ist
Diese Schreibweise bezeichnet nach der oben gegebenen Darstellung den Grenzwert der Folge
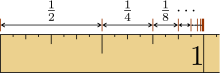
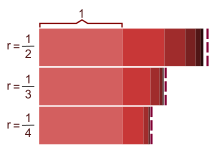
Man kann die Konvergenz dieser Reihe auf der Zahlengeraden visualisieren: Stellen wir uns eine Linie mit der Länge zwei vor, auf der aufeinanderfolgende Abschnitte mit den Längen 1, 1/2, 1/4 usw. markiert sind. Es gibt auf dieser Linie immer noch Platz für einen weiteren Abschnitt, da immer noch so viel Platz ist, wie der letzte Abschnitt lang war: Wenn wir die Strecke 1/2 markiert haben, haben wir insgesamt 3/2 verbraucht, es bleiben also noch 1/2 übrig. Wenn wir nun 1/4 wegstreichen, bleibt ein weiteres 1/4 übrig etc. Da das „Reststück“ beliebig klein wird, ist der Grenzwert gleich 2.
Konvergente geometrische Reihen sind auch ein Gegenstand der Paradoxa von Zenon.
Ein Beispiel für eine divergente Reihe mit mehreren Häufungspunkten ist die Summe über die Folge +1, −1, +1, −1, … Die Reihe wechselt zwischen den Werten 1 und 0 (die Folge hingegen wechselt zwischen 1 und −1).
Semantik
Dem Symbol
kommen zwei unterschiedliche Bedeutungen zu, zwischen denen aus dem Kontext heraus entschieden werden muss. Einmal steht das Symbol für den Wert der Reihe, der im Fall konvergenter Reihen existiert oder im Fall divergenter Reihen nicht existiert:
.
Andererseits repräsentiert das Symbol die Reihe als Folge der Partialsummen, unabhängig vom Konvergenzverhalten:
.
Fast immer ist mit dem Symbol der Grenzwert gemeint. Wenn man die Folge der Partialsummen meinen möchte, benutzt man Wendungen wie „…die Reihe, betrachtet als Folge ihrer Partialsummen,…“
Rechnen mit Reihen
Im Gegensatz zu gewöhnlichen (endlichen) Summen gelten für Reihen einige übliche Regeln der Addition nur bedingt. Man kann also nicht bzw. nur unter bestimmten Voraussetzungen mit ihnen wie mit endlichen Summenausdrücken rechnen.
Summen und Vielfache
Man kann konvergente Reihen gliedweise addieren, subtrahieren oder mit einem festen Faktor (aber nicht einer anderen Reihe) multiplizieren (vervielfachen). Die resultierenden Reihen sind ebenfalls konvergent, und ihr Grenzwert ist die Summe bzw. Differenz der Grenzwerte der Ausgangsreihen bzw. das Vielfache des Grenzwertes der Ausgangsreihe. D.h.
- IMG class="text" style="width: 21.48ex; height: 6.84ex; vertical-align: -3ex;" alt="\sum _{{i=0}}^{\infty }A\cdot a_{i}=A\cdot \sum _{{i=0}}^{\infty }a_{i}" src="/svg/e92938948a7db7a27ad6e51bde91483a55acb312.svg">
Produkte
Man kann absolut konvergente Reihen gliedweise miteinander multiplizieren. Die Produktreihe ist ebenfalls absolut konvergent und ihr Grenzwert ist das Produkt der Grenzwerte der Ausgangsreihen. D.h.
Da die Schreibweise (auf der linken Seite der Gleichung) der Produktreihe mit zwei Indizes in bestimmten Zusammenhängen „unhandlich“ ist, wird die Produktreihe auch in Form des Cauchyprodukts geschrieben. Der Name ergibt sich daraus, dass die Glieder der Produktreihe mit Hilfe des cauchyschen Diagonalverfahrens gebildet werden, dabei werden die Glieder der Ausgangsfolgen in einem quadratischen Schema paarweise angeordnet, und die (durchnummerierten) Diagonalen dieses Schemas bilden die Produktglieder. Für die Produktreihe braucht man dann nur noch einen einzelnen Index. Die Produktreihe hat dann die folgende Form:
Rechnen innerhalb der Reihe
Klammerung (Assoziativität)
Man kann innerhalb einer konvergenten Reihe die Glieder beliebig durch Klammern zusammenfassen. Man kann also beliebig viele Klammern in den „unendlichen Summenausdruck“ einfügen, man darf sie nur nicht innerhalb eines (aus mehreren Termen zusammengesetzten) Gliedes setzen. Der Wert der Reihe ändert sich durch die zusätzlich eingefügte Klammerung dann nicht.
Dies gilt für divergente Reihen im Allgemeinen nicht, was man leicht am folgenden Beispiel erkennt.
Die Reihe
divergiert, während die beklammerte Reihe
gegen Null konvergiert und die anders beklammerte Reihe
gegen noch eine andere Zahl konvergiert.
Andererseits kann man aber keine Klammern ohne Weiteres weglassen. Man kann das aber immer dann, wenn die resultierende Reihe wieder konvergent ist. In diesem Falle bleibt auch der Reihenwert unverändert. Falls die „minderbeklammerte“ Reihe nämlich konvergent ist, kann man ihr dieselben Klammern wieder hinzufügen, die man zuvor weggenommen hat, und die Gleichheit des Grenzwertes ergibt sich nach dem oben Gesagten, wenn man darin die Rollen vertauscht und die „minderbeklammerte“ Reihe nun als Reihe betrachtet, der man Klammern hinzufügt.
Umordnung (Kommutativität)
Eine Umordnung einer Reihe wird durch eine Permutation
ihrer Indexmenge dargestellt. Ist die Indexmenge zum Beispiel (wie meist) die
Menge
der natürlichen Zahlen und
,
eine bijektive
Abbildung der natürlichen Zahlen auf sich, so heißt
eine Umordnung der Reihe
Man kann konvergente Reihen unter Beibehaltung ihres Wertes dann und nur dann beliebig umordnen, wenn sie unbedingt bzw. absolut konvergent sind. Es gilt für unbedingt (oder absolut) konvergente Reihen:
für alle bijektiven
.
Bedingt konvergente Reihen dürfen nur endlich umgeordnet werden, d.h.
ab einem gewissen Index muss für die Umordnung
gelten.
Absolute und unbedingte Konvergenz
Eine Reihe
heißt absolut
konvergent, wenn die Reihe ihrer Absolutglieder
konvergiert.
Eine konvergente Reihe wird formal als unbedingt konvergent definiert, wenn jede ihrer Umordnungen wieder konvergiert und denselben Grenzwert hat. Die letzte Eigenschaft braucht jedoch nicht vorausgesetzt zu werden, da jede Reihe, deren sämtliche Umordnungen konvergent sind, auch für jede Umordnung denselben Wert hat. Eine konvergente Reihe, die nicht unbedingt konvergent ist, heißt bedingt konvergent.
In endlich-dimensionalen Räumen gilt der Satz:
- Eine Reihe ist genau dann unbedingt konvergent, wenn sie absolut konvergent ist.
Für eine bedingt konvergente Reihe kann man eine beliebige Zahl vorgeben und dann eine Umordnung dieser Reihe finden, die gegen genau diese Zahl konvergiert (riemannscher Umordnungssatz). Insbesondere kann man als Zahl auch keine Zahl vorgeben, soll heißen, dass die Reihe divergieren solle, und findet eine geeignete Umordnung, die das tut.
Konvergenzkriterien
Im Folgenden seien die Zahlen
stets reelle oder komplexe Zahlen, und die Reihe
definiert als
Zum Beweis der Konvergenz dieser Reihe gibt es diverse Konvergenzkriterien, die teils die bedingte, teils die stärkere absolute Konvergenz (Konvergenz der Reihe der Beträge der Glieder) zeigen:
Wenn die Reihe
konvergiert, dann konvergiert die Folge (
)
der Summanden für
gegen 0. Formuliert: Ist (
)
keine Nullfolge, so divergiert die
entsprechende Reihe.
Die Umkehrung ist nicht allgemeingültig (ein
Gegenbeispiel ist die harmonische
Reihe).
Wenn alle Glieder
der Reihe
nichtnegative reelle Zahlen sind,
konvergiert und für alle
mit reellen oder komplexen Zahlen
gilt, dann konvergiert auch die Reihe
absolut, und es ist .
Wenn alle Glieder
der Reihe
nichtnegative reelle Zahlen sind,
divergiert und für alle
mit nichtnegativen reellen Zahlen
gilt, dann divergiert auch die Reihe
.
Wenn eine Konstante
und ein Index
existiert, sodass für alle
gilt
dann konvergiert die Reihe
absolut.
Wenn eine Konstante
und ein Index
existiert, sodass für alle
gilt
dann konvergiert die Reihe
absolut.
Ist
eine nichtnegative, monoton fallende
Funktion mit
für alle
,
dann konvergiert
genau dann, wenn das Integral
existiert.
Eine Reihe der Form
mit nichtnegativen
wird alternierende
Reihe genannt. Eine solche Reihe konvergiert, wenn die Folge
monoton gegen 0 konvergiert. Die Umkehrung ist nicht allgemeingültig.
Beispiele
- Eine geometrische
Reihe
konvergiert genau dann, wenn
.
- Die Dirichletreihe
konvergiert für
und divergiert für
, was mit dem Integralkriterium gezeigt werden kann. Als Funktion von
aufgefasst, ergibt diese Reihe die Riemannsche Zetafunktion.
- Die Teleskopreihe
konvergiert genau dann, wenn die Folge
für
gegen eine Zahl
konvergiert. Der Wert der Reihe ist dann
.
Anwendungen
Darstellung mathematischer Konstanten
Neben der Konvergenz und dem numerischen Wert einer Reihe ist auch der
symbolische Wert einer Reihe von Bedeutung. Beispielsweise lassen sich so
mathematische
Konstanten darstellen
und numerisch berechnen. Beispiel für
(natürlicher
Logarithmus)
Für wichtige Reihendarstellungen existieren Tabellierungen in Reihentafeln.
Reihen von Funktionen
Anstatt Folgen von Zahlen kann man auch Folgen von Funktionen betrachten und entsprechend Reihen definieren. Hier kommt zur Frage der Konvergenz noch die nach den Eigenschaften der Grenzfunktion hinzu. Umgekehrt kann man fragen, durch welche Reihe sich eine Funktion darstellen lässt. So eine Darstellung nennt sich Reihenentwicklung.
Potenzreihen
Einige wichtige Funktionen können als Taylorreihen dargestellt werden. Diese sind bestimmte unendliche Reihen, in denen Potenzen einer unabhängigen Variable vorkommen. Solche Reihen werden allgemein Potenzreihen genannt. Werden auch negative Potenzen der Variablen zugelassen, spricht man von Laurentreihen.
Fourierreihen
Als Fourierreihe einer
Funktion bezeichnet man ihre Entwicklung nach trigonometrischen Funktionen
und
.
Die Eulersche
Reihe ist ebenfalls von diesem Typ.
Dirichletreihen
Als Dirichletreihe bezeichnet man eine Entwicklung
mit
Ein wichtiges Beispiel ist die Reihendarstellung der Riemannschen Zetafunktion
mit
.
Präfixsumme
In der Informatik wird mit Präfixsumme
ein Algorithmus bezeichnet, der jeden Eintrag
eines Arrays durch die Partialsumme
ersetzt.
Die Präfixsumme kann parallelisiert
werden und ist daher ein grundlegender Algorithmus für Rechnersysteme mit
mehreren Prozessorkernen,
GPUs
oder Rechnerclustern.
Literatur
- Konrad Knopp: Theorie und Anwendung der unendlichen Reihen. 6. Auflage. Springer, Berlin u. a. 1996, ISBN 3-540-59111-7, Die Grundlehren der mathematischen Wissenschaften in Einzeldarstellungen 2).
- Izrail Solomonovic Gradshteyn, Iosif Mojseevic Ryzhik: Table of Integrals, Series and Products. Herausgegeben von Alan Jeffrey und Daniel Zwillinger. 7. edition. Elsevier Academic Press, Amsterdam u. a. 2007, ISBN 978-0-12-373637-6.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 02.06. 2021