
Unendlichkeit
Der Begriff Unendlichkeit bezeichnet ein mathemarisches Objekt, welches kein Ende
oder Schluss hat, aber einen Anfang oder Beginn haben kann, in der Geometrie
würde also ein Strahl oder eine Kreisbahn als unendlich beschrieben werden.
Sein mathematisches
Symbol ist das Unendlichzeichen
.
Präzisierung fand der Unendlichkeitsbegriff wesentlich durch das Werk Bernard Bolzanos, Georg Cantors und Richard Dedekinds, welches in die Mengenlehre und insbesondere in die Theorie der unendlichen Mengen und der transfiniten Kardinalzahlen mündete.
Unendlichkeit in der Mathematik
In der Mathematik gibt es keinen definierten Begriff mit dem Namen „Unendlichkeit“, jedoch wird das Adjektiv unendlich zur näheren Charakterisierung einiger mathematischer Begriffe verwendet. In der Regel ist diese Charakterisierung komplementär zum Begriff endlich. Beispiele solcher Begriffsbildungen sind:
- unendliche Menge als komplementärer Begriff zur endlichen Menge,
- unendliche Ordinalzahl,
- unendliche Kardinalzahl,
- unendlichdimensionaler Vektorraum als komplementärer Begriff zum endlichdimensionalen Vektorraum.
Es gibt aber auch Begriffe wie ein unendliches Produkt, dessen Definition weitergehende Eigenschaften als die Nicht-Endlichkeit der Faktorenanzahl beinhaltet. Ähnlich verhält es sich mit den Begriffen einer unendlich großen Nicht-Standardzahl und eines unendlichen Grenzwertes.
Ein Beispiel für eine redundante Verwendung ist der veraltete Begriff der unendlichen Reihe, kurz Reihe.
Unendliche Werte werden in der Mathematik durch das Unendlichzeichen
dargestellt. Dieses Symbol wurde 1655 von dem englischen Mathematiker John Wallis als Zeichen für
eine abstrakte unendliche Größe eingeführt. Beispiele für seine Verwendung
sind:
oder
für unbeschränkte Intervalle,
für den Grenzwert einer konvergenten Folge
,
für den Limes einer Reihe,
bei einem uneigentlichen Integral mit unbeschränktem Integrationsbereich,
für die Maximumsnorm oder die Supremumsnorm.
Unter den unendlichen Mengen gibt es noch Abstufungen:
- So sagt man, dass eine Menge fast alle Elemente einer unendlichen Grundmenge enthält, wenn sie alle Elemente bis auf endlich viele Ausnahmen enthält. Eng damit verwandt ist bei einem Maßraum der Begriff des fast sicheren Ereignisses. Mengen dieser beiden Typen sind (bei unendlichen Grundmengen) stets unendliche Mengen. Die Umkehrung gilt aber nicht.
- Auch unter den unendlichen Kardinal- und Ordinalzahlen gibt es Abstufungen, die sich in Größenbeziehungen widerspiegeln. Diese entsprechen Inklusionsrelationen der zugrundeliegenden Mengen.
Sowohl bei der Kompaktifizierung eines topologischen Raumes als auch bei der Konstruktion einer projektiven Geometrie werden Mengen um Elemente erweitert, die man aufgrund der intuitiven Vorstellung als unendlich ferne Punkte bezeichnet.
In den bisherigen Beispielen von Begriffen stand das Adjektiv unendlich in seiner intuitiven Wortbedeutung für unendlich groß, unendlich viele beziehungsweise unendlich weit entfernt. Namensgebend für die Infinitesimalrechnung waren historisch verwendete unendlich kleine Größen, wobei es einen großen, insbesondere auf Karl Weierstraß zurückgehenden Fortschritt bedeutete, solche Konstruktion zu vermeiden.
Unendliche Menge
Eine unendliche Menge
ist eine Menge, die nicht endlich ist. Bei einer Menge
ist das gleichbedeutend damit, dass es keine natürliche
Zahl
gibt, für die eine Bijektion,
das heißt eine „eins-zu-eins-Zuordnung“,
existiert.
Die Existenz unendlicher Mengen ist Gegenstand des Unendlichkeitsaxioms der axiomatisch begründeten Zermelo-Fraenkel-Mengenlehre.
Analysis: Bestimmte Divergenz
Eine Folge
reeller Zahlen weist eine bestimmte
Divergenz gegen unendlich auf, wenn jede beliebig vorgegebene reelle Zahl
von fast allen Folgengliedern überschritten wird. Symbolisch schreibt man in
diesem Fall, in dem man auch von einer uneigentlichen Konvergenz spricht,
auch
Analog schreibt man im Fall einer bestimmten Divergenz gegen minus unendlich
Für solche Sachverhalte lassen sich auch „Rechenregeln“ formulieren wie
Eine solche Rechenregel muss aber stets als Aussage über uneigentliche Grenzwerte verstanden werden. So steht die gerade angeführte Rechenregel für den folgenden Sachverhalt:
- Sind
und
zwei Folgen reeller Zahlen, so dass
gegen
konvergiert und
bestimmt gegen unendlich divergiert, dann divergiert auch die Folge
bestimmt gegen unendlich.
Kompaktifizierungen
Uneigentliche Grenzwerte lassen sich im Blickwinkel der Topologie im
Rahmen einer sogenannten Kompaktifizierung als Grenzwert auffassen, nun aber in
einem topologischen Raum ,
bei dem die reellen Zahlen
um zwei Elemente erweitert werden. Dabei kann man sich die beiden
hinzugenommenen Elemente intuitiv als unendlich entfernte Punkte auf dem Zahlenstrahl
vorstellen.
Zu beachten ist aber, dass es auf der so erweiterten Menge nicht möglich ist,
arithmetische Operationen mit den bekannten Rechenregeln zu definieren. Auch
gibt es andere Kompaktifizierungen, die in Bezug auf die Konvergenz von Folgen
zu anderen Aussagen führen. Ein Beispiel ist die Einpunktkompaktifizierung
mit nur einem zusätzlichen, „unendlichen“ Element. Dort konvergiert die
Folge
die aber nicht in der Kompaktifizierung
konvergiert.
Eine Kompaktifizierung eines topologischen Raumes eignet sich auch zur Untersuchung von stetigen Funktionen, die auf diesem topologischen Raum definiert sind. Dazu müssen die betreffenden Funktionen auf die Kompaktifzierung stetig fortgesetzt werden können.
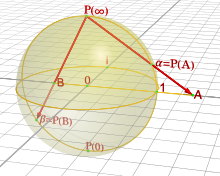
Im Bereich der Funktionentheorie
wird zur Untersuchung von holomorphen
und meromorphen
Funktionen die Einpunktkompaktifizierung
verwendet, die man auch als Riemannsche
Zahlenkugel bezeichnet.
Eine Verallgemeinerung der Einpunktkompaktifizierung
der reellen Zahlen (und entsprechend von
)
ist der
-dimensionale
projektive
Raum
.
Er entsteht aus dem
-dimensionalen
euklidischen Raum
durch Punkte, die man intuitiv als unendlich fern auffassen kann und die
mit den Geraden durch den Nullpunkt korrespondieren.
Zur Konstruktion des projektiven Raums:
ist definiert als Menge aller Geraden durch den Nullpunkt des
.
Eine Einbettung
des euklidischen Raums
in den projektiven Raum
ergibt sich dadurch, dass man einerseits den
mit einer affinen
Hyperebene im
,
die nicht den Nullpunkt enthält, identifiziert und andererseits die durch den
Nullpunkt verlaufenden Geraden im
,
die nicht parallel zu dieser affinen Hyperebene liegen, mit ihren Schnittpunkten
mit dieser Hyperebene.
Projektive Ebene
Die gerade beschriebene Konstruktion kann im Fall der euklidischen Ebene
auch im Sinne der affinen
Geometrie interpretiert werden. Dabei wird jede Gerade um einen „unendlich
fernen“ Punkt erweitert, nämlich durch den Punkt, der durch diejenige Gerade
durch den Nullpunkt repräsentiert wird, die zur gegebenen Gerade parallel
verläuft. Damit schneiden sich zwei Parallelen, die von der euklidischen Ebene
auf die projektive
Ebene erweitert werden, in diesem gemeinsamen unendlich
fernen Punkt.
Nichtstandardanalysis
Grundlage der Nichtstandardanalysis ist der geordnete Körper der hyperreellen Zahlen, der die reellen Zahlen als Teilkörper enthält. Der Körper der hyperrellen Zahlen enthält sowohl infinitesimal benachbarte Zahlen wie auch unendlich große Zahlen.
Unendlich große Zahlen gibt es auch in der Klasse der surrealen Zahlen und in der Unterklasse der kombinatorischen Spiele. Dabei bilden die hyperrellen Zahlen eine Teilmenge der surrealen Zahlen.
Kardinalzahlen
Wie bei endlichen Mengen können auch zwei unendliche Mengen daraufhin untersucht werden, ob sie die gleiche Mächtigkeiten besitzen. Dies ist per Definition genau dann der Fall, wenn es eine Bijektion zwischen ihnen gibt. Mengen gleicher Mächtigkeit werden durch eine übereinstimmende Kardinalzahl gekennzeichnet. Bei einer endlichen Mengen handelt es sich bei der Kardinalzahl um die Anzahl der Elemente.
Unterschiedliche Mächtigkeiten besitzen insbesondere die beiden Mengen der natürlichen und reellen Zahlen, was erstmals von Georg Cantor, dem Begründer der Mengenlehre, bewiesen wurde. Der einfachste Beweis verwendet Cantors zweites Diagonalargument, das dahingehend verallgemeinert werden kann, dass eine Menge stets eine andere Mächtigkeit besitzt als ihre Potenzmenge.
Die Kardinalzahl der Menge der natürlichen Zahlen besitzt unter Verwendung
des hebräischen Buchstabens
(Aleph) die
Bezeichnung
.
Mengen dieser Kardinalität heißen abzählbar.
Unendliche Mengen, die nicht abzählbar sind, heißen überabzählbar.
Die Kardinalzahl der reellen Zahlen ist
,
weil die Menge der reellen Zahlen gleichmächtig zur Potenzmenge der natürlichen
Zahlen ist.
Die beiden wichtigste Beispiele für abzählbare Mengen sind (neben der Menge der natürlichen und der ganzen Zahlen) die Menge der rationalen Zahlen (Beweis mit Cantors erstem Diagonalargument) und dann noch die Menge der algebraischen Zahlen. Mit letzterem Beispiel und der Erkenntnis, dass nur abzählbar viele algebraischen Zahlen existieren, ist, da die Menge der reellen Zahlen überabzählbar ist, einer der ersten großen Triumphe Georg Cantors (gefunden 1874) und der Mengenlehre verbunden. Denn dies zieht nach sich, dass nicht alle reellen Zahlen algebraisch sein können, und führt folglich zu dem Nachweis, dass es transzendente Zahlen geben muss.
Bereits Cantor vermutete die sogenannte Kontinuumshypothese, gemäß der jede Teilmenge der reellen Zahlen entweder abzählbar oder gleichmächtig zur Menge der reellen Zahlen ist.
Ordinalzahlen
Wie bei Kardinalzahlen kann auch jede Ordinalzahl durch eine Menge repräsentiert werden. Betrachtet werden allerdings nur wohlgeordnete Mengen, wobei zwei Mengen, zwischen denen ein Ordnungsisomorphismus existiert, die gleiche Ordinalzahl definieren. Zum Beispiel repräsentieren die beiden Mengen mit den Elementen
bzw.
übereinstimmend die Ordinalzahl .
Die Ordinalzahl
wird repräsentiert durch die Menge, die die Elemente
enthält. Die Ordinalzahl
lässt sich mit der Menge repräsentieren, die die (in Anbetracht ihrer
Bezeichnung abweichend vom Standard geordneten) Elemente
enthält.
Kontroversen über die Existenz nicht endlicher Mengen
Die vorstehend beschriebenen Begriffe sind in Bezug darauf, ob, auf welcher Basis und wie solche Begriffe formal definiert werden können, Gegenstand historischer Kontroversen über grundlegende Annahmen der Mathematik gewesen. Heute gilt als bewährter und weithin akzeptierter Rahmen für die Mathematik die Zermelo-Fraenkel-Mengenlehre inklusive des Auswahlaxioms (abgekürzt ZFC), auch wenn deren Widerspruchsfreiheit aufgrund von Gödels Zweitem Unvollständigkeitssatz nicht beweisbar ist. Abseits dieses „Mainstreams“ existieren aber weitere „Schulen“ von Konstruktivisten, Finitisten und Ultrafinitisten, die ihre parallele Berechtigung in einem Verzicht auf bestimmte Axiome oder Schlussweisen finden.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 17.12. 2020