
Holomorphe Funktion
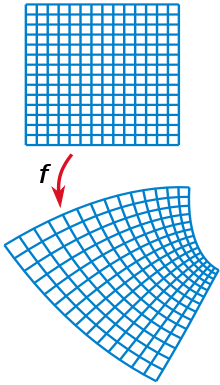
Holomorphie (von gr.
ὅλος holos, „ganz“ und μορφή morphe, „Form“) ist eine Eigenschaft
von bestimmten komplexwertigen
Funktionen, die in der Funktionentheorie
(einem Teilgebiet
der Mathematik) behandelt
werden. Eine Funktion
mit einer offenen
Menge
heißt holomorph, falls sie in jedem Punkt von
komplex differenzierbar ist. Insbesondere in älterer Literatur werden solche
Funktionen auch regulär genannt.
Auch wenn die Definition analog zur reellen Differenzierbarkeit ist, zeigt sich in der Funktionentheorie, dass die Holomorphie eine sehr starke Eigenschaft ist. Sie produziert nämlich eine Vielzahl von Phänomenen, die im Reellen kein Pendant besitzen. Beispielsweise ist jede holomorphe Funktion beliebig oft (stetig) differenzierbar und lässt sich lokal in jedem Punkt in eine Potenzreihe entwickeln.
Definitionen
Es sei
eine offene Teilmenge der komplexen Ebene und
ein Punkt dieser Teilmenge. Eine Funktion
heißt komplex differenzierbar im Punkt
,
falls der Grenzwert
existiert. Man bezeichnet ihn dann als .
Die Funktion
heißt holomorph im Punkt
,
falls eine Umgebung
von
existiert, in der
komplex differenzierbar ist. Ist
auf ganz
holomorph, so nennt man
holomorph. Ist weiter
,
so nennt man
eine ganze
Funktion.
Erläuterungen
Zusammenhang zwischen komplexer und reeller Differenzierbarkeit
ist in natürlicher Weise ein zweidimensionaler reeller Vektorraum mit der
kanonischen Basis
und so kann man eine Funktion
auf einer offenen Menge
auch auf ihre totale
Differenzierbarkeit im Sinne der mehrdimensionalen
reellen Analysis untersuchen. Bekanntlich heißt
(total) differenzierbar
in
,
falls eine
-lineare
Abbildung
existiert, sodass
gilt, wobei
eine Funktion mit
ist. Nun sieht man, dass die Funktion
genau dann in
komplex differenzierbar ist, wenn sie dort total differenzierbar ist und
sogar
-linear
ist. Letzteres ist eine starke Bedingung. Sie bedeutet, dass die Darstellungsmatrix
von
bezüglich der kanonischen Basis
die Form
hat.
Cauchy-Riemannsche Differentialgleichungen
Zerlegt man nun eine Funktion
in ihren Real- und Imaginärteil mit reellen Funktionen
,
so hat die totale Ableitung
als Darstellungsmatrix die Jacobi-Matrix
Folglich ist die Funktion
genau dann komplex differenzierbar, wenn sie reell differenzierbar ist und für
die Cauchy-Riemannschen Differentialgleichungen
erfüllt sind.
Äquivalente Eigenschaften holomorpher Funktionen einer Variablen
In einer Umgebung einer komplexen Zahl sind folgende Eigenschaften komplexer Funktionen gleichwertig:
- Die Funktion ist einmal komplex differenzierbar.
- Die Funktion ist beliebig oft komplex differenzierbar.
- Real- und Imaginärteil erfüllen die Cauchy-Riemannschen Differentialgleichungen und sind zumindest einmal stetig reell-differenzierbar.
- Die Funktion lässt sich in eine komplexe Potenzreihe entwickeln.
- Die Funktion ist stetig und das Wegintegral der Funktion über einen beliebigen geschlossenen zusammenziehbaren Weg verschwindet.
- Die Funktionswerte im Inneren einer Kreisscheibe lassen sich aus den Funktionswerten am Rand mit Hilfe der cauchyschen Integralformel ermitteln.
- Die Funktion
ist reell differenzierbar und es gilt
wobeider Cauchy-Riemann-Operator ist, der durch
definiert ist.
Beispiele
Ganze Funktionen
Ganze Funktionen sind auf ganz
holomorph. Beispiele dafür sind
- jedes Polynom
mit Koeffizienten
,
- die Exponentialfunktion
,
- die trigonometrischen
Funktionen
und
,
- die hyperbolischen
Funktionen
und
.
Holomorphe, nichtganze Funktionen
- Gebrochen rationale Funktionen sind holomorph außer an den Nullstellen ihres Nennerpolynoms. Dort besitzen sie isolierte Singularitäten. Wenn diese nicht hebbar sind, handelt es sich um Polstellen, sodass dann Beispiele für meromorphe Funktionen vorliegen.
- Die Logarithmusfunktion
lässt sich in allen Punkten aus
in eine Potenzreihe entwickeln und ist somit auf der Menge
holomorph.
Nirgends holomorphe Funktionen
In keinem
komplex differenzierbar und damit auch nirgendwo holomorph sind beispielsweise
- die Betragsfunktion
,
- die Projektionen auf den Realteil
beziehungsweise auf den Imaginärteil
,
- die komplexe Konjugation
.
Die Funktion
ist nur an der Stelle
komplex differenzierbar, aber dort nicht holomorph, da sie nicht in einer
ganzen Umgebung von
komplex differenzierbar ist.
Eigenschaften
Sind
an einer Stelle
komplex differenzierbar, so auch
,
und
.
Das gilt auch für
,
wenn
keine Nullstelle von
ist. Es gelten ferner Summen-,
Produkt-, Quotienten- und Kettenregel.
Es folgt eine Auflistung fundamentaler Eigenschaften holomorpher Funktionen,
die alle keine Entsprechung in der reellen Theorie besitzen. In der Folge sei
ein Gebiet
und
holomorph.
Cauchyscher Integralsatz
Ist
einfach
zusammenhängend und
ein Zyklus
in
,
so gilt der cauchysche
Integralsatz
Der Satz gilt also insbesondere dann, wenn
ein Sterngebiet und
ein geschlossener
Weg ist.
Cauchysche Integralformel
Sei
die offene Kreisscheibe mit Radius
um den Punkt
.
Liegt der Abschluss
von
noch ganz in
,
so gilt für alle
und
die cauchysche Integralformel
Der Wert der Funktion (und jeder ihrer Ableitungen) eines Punktes in einem Gebiet hängt also nur von den Funktionswerten am Rand dieses Gebietes ab.
Holomorphie und Analytizität
Eine Folgerung aus der cauchyschen Integralformel ist, dass in der komplexen
Ebene der Begriff der Analytizität
äquivalent zur Holomorphie ist: Jede in
holomorphe Funktion ist in
analytisch.
Umgekehrt lässt sich jede in
analytische Funktion zu einer in
holomorphen Funktion fortsetzen.
Da Potenzreihen beliebig oft komplex differenzierbar sind (und zwar durch gliedweise Differentiation), erhält man insbesondere, dass holomorphe Funktionen beliebig oft differenzierbar und alle ihre Ableitungen wiederum holomorphe Funktionen sind. Hieran erkennt man schon deutliche Unterschiede zur reellen Differentialrechnung.
Identitätssatz
Es zeigt sich, dass eine holomorphe Funktion schon durch sehr wenig
Information eindeutig bestimmt ist. Der Identitätssatz
besagt, dass zwei holomorphe Funktionen auf einem Gebiet
bereits dann auf ganz
identisch sind, wenn sie auf einer geeigneten echten Teilmenge
übereinstimmen. Dabei muss die Übereinstimmungsmenge
noch nicht einmal ein kontinuierlicher Weg
sein: Es reicht aus, dass
einen Häufungspunkt
in
besitzt. Diskrete
Teilmengen reichen hierfür hingegen nicht aus.
Weiteres
- Der Satz von Liouville besagt, dass jede beschränkte ganze Funktion konstant ist. Eine einfache Folgerung hieraus ist der Fundamentalsatz der Algebra.
- Satz
von der Gebietstreue: Ist
ein Gebiet und
nicht konstant, dann ist
wieder ein Gebiet.
- Eine Folgerung der Gebietstreue ist das Maximumprinzip.
- Satz
von Weierstraß: Konvergiert eine Folge
holomorpher Funktionen kompakt auf
gegen die Grenzfunktion
, so ist
wieder holomorph und man kann Limesbildung und Differentiation vertauschen, das heißt, die Folge
konvergiert kompakt gegen
.
- Satz
von Montel: Ist die Folge
holomorpher Funktionen auf
lokal beschränkt, so existiert eine kompakt konvergente Teilfolge.
- Jede auf einem einfach
zusammenhängenden Gebiet
zweimal stetig differenzierbare harmonische Funktion
ist Realteil einer komplex differenzierbaren Funktion
. Die reelle Funktion
erfüllt ebenfalls
. Sie wird als konjugiert harmonisch zu
bezeichnet und
als komplexes Potential.
Biholomorphe Funktionen
Eine Funktion, die holomorph, bijektiv und deren Umkehrfunktion holomorph ist, nennt man biholomorph. Im Fall einer komplexen Veränderlichen ist das äquivalent dazu, dass die Abbildung bijektiv und konform ist. Aus dem Satz über implizite Funktionen folgt für holomorphe Funktionen einer Veränderlicher schon, dass eine bijektive, holomorphe Funktion stets eine holomorphe Umkehrabbildung besitzt. Im nächsten Abschnitt werden holomorphe Funktionen mehrerer Veränderlicher eingeführt. In diesem Fall garantiert der Satz von Osgood diese Eigenschaft. Somit kann man sagen, dass bijektive, holomorphe Abbildung biholomorph sind.
Aus Sicht der Kategorientheorie ist eine biholomorphe Abbildung ein Isomorphismus.
Holomorphie mehrerer Veränderlicher
Im n-dimensionalen komplexen Raum
Sei
eine offene Teilmenge. Eine Abbildung
heißt holomorph, falls sie sich um jeden Punkt des Definitionsbereichs in eine
Potenzreihe entwickeln lässt, das heißt, zu jedem
gibt es einen Polykreis
,
sodass
für alle
mit von
unabhängigen Koeffizienten
gilt. Eine Funktion
heißt holomorph in der
-ten
Variablen, wenn sie als Funktion von
bei festgehaltenen übrigen Variablen holomorph ist. Holomorphe Funktionen sind
natürlich in jeder Variablen holomorph. Für die Umkehrung siehe die
untenstehenden äquivalenten Charakterisierungen.
Mit dem Wirtinger-Kalkül
und
steht ein Kalkül zur Verfügung, mit dem man die partiellen Ableitungen einer
komplexen Funktion wie bei Funktionen einer Veränderlichen behandeln kann.
Für eine Funktion ,
offen, sind folgende Aussagen äquivalent:
ist holomorph.
ist stetig und holomorph in jeder Variablen (Lemma von Osgood)
ist holomorph in jeder Variablen (Satz von Hartogs)
ist stetig differenzierbar und genügt den cauchy-riemannschen Differentialgleichungen
für
.
Für mehrere Dimensionen im Bildbereich definiert man Holomorphie wie folgt:
Eine Abbildung ,
offen, heißt holomorph, wenn jede der Teilfunktionen
holomorph ist.
Viele Eigenschaften holomorpher Funktionen einer Veränderlichen lassen sich,
teils in abgeschwächter Form, auf den Fall mehrerer Veränderlicher übertragen.
So gilt für Funktionen
der cauchysche Integralsatz nicht und der Identitätssatz
ist nur noch in einer abgeschwächten Version gültig. Für diese Funktionen kann
allerdings die Integralformel von Cauchy durch Induktion
auf
Dimensionen verallgemeinert werden. Salomon
Bochner konnte 1944 sogar noch eine Verallgemeinerung der
-dimensionalen
cauchyschen Integralformel beweisen. Diese trägt den Namen Bochner-Martinelli-Formel.
In der komplexen Geometrie
Auch in der komplexen Geometrie werden holomorphe Abbildungen betrachtet. So kann man holomorphe Abbildungen zwischen riemannschen Flächen oder zwischen komplexen Mannigfaltigkeiten analog zu differenzierbaren Funktionen zwischen glatten Mannigfaltigkeiten definieren. Außerdem gibt es ein für die Integrationstheorie wichtiges Pendant zu den glatten Differentialformen, das holomorphe Differentialform heißt.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 08.12. 2020