Harmonische Funktion

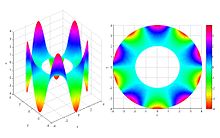
Eine harmonische Funktion definiert auf einem Kreisring.

In der Analysis heißt eine reellwertige, zweimal stetig differenzierbare Funktion harmonisch, wenn die Anwendung des Laplace-Operators auf die Funktion null ergibt, die Funktion also eine Lösung der Laplace-Gleichung ist. Das Konzept der harmonischen Funktionen kann man auch auf Distributionen und Differentialformen übertragen.

Definition

Sei $U\subseteq \mathbb {R} ^{n}$ eine offene Teilmenge. Eine Funktion $f\colon U\rightarrow \mathbb {R}$ heißt harmonisch in , falls sie zweimal stetig differenzierbar ist und für alle $x\in U$

$\Delta f(x)=0$

gilt. Dabei bezeichnet $\Delta ={\tfrac {\partial ^{2}}{\partial x_{1}^{2}}}+{\tfrac {\partial ^{2}}{\partial x_{2}^{2}}}+\cdots +{\tfrac {\partial ^{2}}{\partial x_{n}^{2}}}$ den Laplace-Operator.

Mittelwerteigenschaft

Die wichtigste Eigenschaft harmonischer Funktionen ist die Mittelwerteigenschaft, welche äquivalent ist zur Definition:

Eine stetige Funktion $f\colon U\rightarrow \mathbb {R}$ ist genau dann harmonisch, wenn sie die Mittelwerteigenschaft erfüllt, das heißt, wenn

$f(x)={\frac {1}{r^{n-1}s_{n-1}}}\int _{\partial B(x,r)}f(y)\mathrm {d} \sigma (y)$

für alle Kugeln $\ B(x,r)$ mit ${\overline {B}}(x,r)\subset U$ . Hierbei bezeichnet $\ s_{n-1}$ das Oberflächenmaß der n-1 -dimensionalen Einheitssphäre.

Weitere Eigenschaften

Die weiteren Eigenschaften der harmonischen Funktionen sind größtenteils Konsequenzen der Mittelwerteigenschaft.

Maximumprinzip: Im Innern eines zusammenhängenden Definitionsgebietes nimmt eine harmonische Funktion ihr Maximum und ihr Minimum nie an, außer wenn sie konstant ist. Besitzt die Funktion zudem eine stetige Fortsetzung auf den Abschluss ${\overline {U}}$ , so werden Maximum und Minimum auf dem Rand $\partial U$ angenommen.
Glattheit: Eine harmonische Funktion ist beliebig oft differenzierbar. Dies ist insbesondere bei der Formulierung mit Hilfe der Mittelwerteigenschaft bemerkenswert, wo nur die Stetigkeit der Funktion vorausgesetzt wird.
Abschätzung der Ableitungen: Sei harmonisch in . Dann gilt für die Ableitungen
$\left|D^{\alpha }f(x)\right|\leq {\frac {\left(2^{n+1}n|\alpha |\right)^{|\alpha |}}{v_{n}}}\left\|f\right\|_{L^{1}(B(x,r))},$
wobei $v_{n}$ das Volumen der -dimensionalen Einheitskugel bezeichnet.
Analytizität: Aus der Abschätzung der Ableitungen folgt, dass jede harmonische Funktion in eine konvergente Taylorreihe entwickelt werden kann.
Satz von Liouville: Eine beschränkte harmonische Funktion $f\colon \mathbb {R} ^{n}\rightarrow \mathbb {R}$ ist konstant.
Harnack-Ungleichung: Für jede zusammenhängende, offene und relativ kompakte Teilmenge $V\subset \subset U$ gibt es eine Konstante $C\geq 0$ , die nur von dem Gebiet abhängt, so dass für jede in harmonische und nichtnegative Funktion
$\sup _{V}f\leq C\inf _{V}f$
gilt.
Im Sonderfall für ein einfach zusammenhängendes Gebiet $U\subset \mathbb {R} ^{2}\cong \mathbb {C}$ können die harmonischen Funktionen als Realteile analytischer Funktionen einer komplexen Variablen aufgefasst werden.
Jede harmonische Funktion ist auch eine biharmonische Funktion.

Beispiel

Die Grundlösung

$S(x):=\left\{{\begin{array}{ll}-{\frac {1}{2\pi }}\ln |x|\ ,&n=2\ ,\\{\frac {1}{(n-2)\omega _{n}}}{\frac {1}{\|x\|^{n-2}}}\ ,&n\geq 3\ ,\\\end{array}}\right.$

ist eine auf $\mathbb {R} ^{n}\setminus \{0\}$ harmonische Funktion, worin $\omega _{n}$ das Maß der Einheitssphäre im $\mathbb {R} ^{n}$ bezeichnet. Versehen mit dieser Normierung spielt die Grundlösung eine fundamentale Rolle in der Theorie zur Poisson-Gleichung.

Verallgemeinerungen

Polyharmonische Funktionen sind bis zur 2m-ten Ordnung der Ableitung stetige Lösungen der Differentialgleichung:

${\Delta }^{m}f=0$

Für m=2 (Biharmonische Funktion) taucht die Differentialgleichung in der Theorie der elastischen Platten auf (Gustav Kirchhoff).

Basierend auf einem Artikel in:

Wikipedia.de