Einheitskugel

Unter der Einheitskugel versteht man in der Mathematik die Kugel mit Radius eins um den Nullpunkt eines Vektorraums. Dabei wird ein verallgemeinerter Begriff des Abstands zugrunde gelegt, so dass je nach Zusammenhang die Einheitskugel keine Ähnlichkeit mehr mit einer herkömmlichen Kugel haben muss. Diese Einheitssphäre ist der Rand der Einheitskugel, im zweidimensionalen reellen Vektorraum mit der euklidischen Norm ist dies der Einheitskreis.
Allgemeine Definition
Es sei
ein normierter
Vektorraum. Dann nennt man die Menge der Punkte, deren Abstand vom Nullpunkt
kleiner als eins ist, die offene
Einheitskugel in
:
Entsprechend bezeichnet
die abgeschlossene
Einheitskugel in
sowie
die Einheitssphäre in .
Mittels Translation und Skalierung lassen sich in einem Raum beliebige Kugeln in die Einheitskugel überführen. Deshalb reicht es oft aus, bestimmte Aussagen nur für die Einheitskugel nachzuweisen, um die Gültigkeit für beliebige Kugeln zu folgern.
Einheitskugel in endlichdimensionalen Räumen
Im Falle des euklidischen
Raumes
definiert man die abgeschlossene Einheitskugel bezüglich der euklidischen Norm
mittels
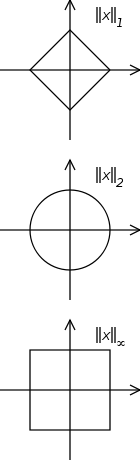
Einheitskugeln können alternativ im
bezüglich anderer Normen
definiert werden, beispielsweise der Summennorm
(1-Norm)
oder der Maximumsnorm
.
Die geometrische Gestalt der Einheitskugel hängt von der gewählten Norm ab und ist nur
mit der euklidischen Norm tatsächlich kugelförmig.
Volumen
Das Volumen einer -dimensionalen,
euklidischen Einheitskugel ist
Hierbei ist
die Gammafunktion,
eine analytische
Fortsetzung der (verschobenen) Fakultät
auf die reellen Zahlen. Für gerades
vereinfacht sich die Formel zu
.
Bemerkenswert ist in diesem Zusammenhang, dass das Volumen der Einheitskugel
in Abhängigkeit von der Raumdimension
bis
zunächst zunimmt, um dann wieder abzufallen – und sogar für
gegen 0 zu gehen:
| Dimension | Volumen der Einheitskugel | Näherung |
|---|---|---|
| 1 | 2 | 2,00 |
| 2 | 3,14 | |
| 3 | 4,19 | |
| 4 | 4,93 | |
| 5 | 5,26 | |
| 6 | 5,17 | |
| 7 | 4,72 | |
| 12 | 1,34 | |
| 20 | 0,0258 | |
| 25 | 0,00096 |
Die Einheitskugel bezüglich der Summennorm ist geometrisch ein Kreuzpolytop, ihr Volumen
beträgt .
Die Einheitskugel bezüglich der Maximumsnorm ist ein Hyperwürfel mit
Kantenlänge 2, hat also das Volumen .
Bemerkungen
- Die Einheitssphäre bildet den Rand der Einheitskugel. Entsprechend ist im zweidimensionalen die Einheitskugel nicht der Kreis, sondern die Kreisscheibe.
- Allgemeiner kann eine Einheitskugel in jedem metrischen Raum
definiert werden. Zu beachten ist, dass dort nicht von vornherein ein Punkt
als Nullpunkt ausgezeichnet sein muss und man deswegen nur bedingt von
der Einheitskugel eines metrischen Raumes sprechen kann. Weiterhin sind
gerade bei Metriken, die nicht norminduziert sind, die Einheitskugeln noch
weiter von der Anschauung entfernt. Speziell gilt in einem Vektorraum
mit der diskreten Metrik:
,
und
.
- Bei der Betrachtung von Umgebungen wird die Einheitskugel auch als 1-Kugel oder 1-Ball bezeichnet.
Eigenschaften
- Die abgeschlossene Einheitskugel
ist konvex. (Die Konvexität folgt aus der Dreiecksungleichung.)
- Sie ist punktsymmetrisch
zum Ursprung 0:
.
- Umgekehrt wird in einem endlichdimensionalen
Vektorraum durch jede abgeschlossene konvexe Menge
, die punktsymmetrisch zum Ursprung liegt und den Ursprung im Inneren enthält, eine Norm definiert, die diese Menge als Einheitskugel hat:
, für
(siehe Minkowski-Funktional).
- Die abgeschlossene Einheitskugel
ist genau dann kompakt, wenn
endlichdimensional ist.
- Die abgeschlossene Einheitskugel
ist genau dann schwach kompakt, wenn
reflexiv ist.
- Die abgeschlossene Einheitskugel
im topologischen Dualraum
von
ist immer schwach-*-kompakt (Satz von Banach-Alaoglu).
Anwendungen in den Naturwissenschaften
In vielfältiger Art wird die Einheitskugel in den Geowissenschaften angewandt, insbesondere für Berechnungen auf der Erdkugel. Sie erfolgen mit sogenannten Kugeldreiecken und den Formeln der Sphärischen Trigonometrie, wenn eine Genauigkeit von etwa 0,1 % genügt, zum Beispiel bei der Geografie und Kartografie, Globenberechnungen und Navigation. Die wahren Distanzen erhält man aus den Kugelbögen durch Multiplikation mit dem Erdradius.
Für höhere Genauigkeit – vor allem in der Geodäsie – ist statt der Erdkugel das Erdellipsoid zu verwenden. Mit der Methode der Verebnung sind aber Dreiecksberechnungen auch sphärisch möglich.
Geologen verwenden für Richtungsanalysen von Gesteinsschichten oder Klüften eine Einheitskugel, die sie Lagenkugel nennen. In sie werden die Normalenvektoren der jeweiligen Ebenen eingetragen und danach in flächentreuer Azimutalprojektion dargestellt.
Auch astronomische Berechnungen werden seit jeher auf der Einheitskugel um den Beobachter durchgeführt. Sie entspricht dem freiäugigen Anblick des Himmelsgewölbes und wird Himmelskugel genannt, auf der die sphärische Astronomie eigene Koordinatensysteme für Winkelmessungen und Sternörter definiert hat. Ob der Kugelradius mit 1 oder mit ∞ angenommen wird, ist dabei ohne Belang.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 07.06. 2024