
Innerer Punkt
Innerer Punkt sowie Inneres bzw. offener Kern sind Begriffe aus der Topologie, einem Teilgebiet der Mathematik.
Jedes Element
einer Teilmenge
eines topologischen
Raums
,
zu dem sich eine Umgebung
in
finden lässt, die vollständig in
liegt, ist ein innerer Punkt von
.
Die Menge aller inneren Punkte von
heißt Inneres oder offener Kern von
.
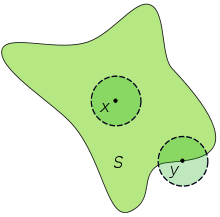
Beispiel: Betrachtet man eine Kreisscheibe als Teil der Ebene, dann sind die Punkte auf dem Rand des Kreises keine inneren Punkte (sondern Randpunkte). Dagegen sind alle Punkte zwischen dem Kreisrand und dem Kreismittelpunkt und der Kreismittelpunkt selbst innere Punkte der Kreisfläche.
Definition
Sei
eine beliebige Teilmenge
eines topologischen
Raums
.
Dann ist ein Punkt
aus
genau dann ein innerer Punkt von
,
wenn
eine Umgebung
von
in
ist, d.h. wenn es eine Teilmenge
gibt, die
enthält und in
offen ist.
Die Menge aller inneren Punkte von
heißt Inneres oder offener Kern von
;
sie ist die größte offene Teilmenge von
.
Sie wird üblicherweise mit
oder insbesondere in englischsprachiger Literatur mit
oder
bezeichnet.
Eigenschaften
- Eine Teilmenge eines topologischen Raumes ist genau dann offen, wenn sie gleich ihrem Inneren ist.
- Das Innere des Komplements ist das Komplement des Abschlusses und umgekehrt:
-
und
Das Innere des Komplements heißt auch das Äußere von M. Der Raum X zerfällt also in Inneres, Rand und Äußeres von M.
Beispiel
Nehme die folgende Menge
und die Zahl
:

ist ein innerer Punkt von
,
weil es ein
gibt, sodass
eine Teilmenge von
ist:

Innere Punkte von Intervallen
- Die inneren Punkte des kompakten
Intervalls
sind genau die zum offenen Intervall
gehörenden Punkte.
- Ebenso sind die inneren Punkte des halboffenen
Intervalls
oder des halboffenen Intervalls
genau die zum offenen Intervall
gehörenden Punkte.
- Alle Punkte des offenen Intervalls
sind innere Punkte.
Siehe auch
- Kernoperator
- Insbesondere im Kontext von konvexen Teilmengen reeller Vektorräume betrachtet man das Innere bezüglich der affinen Hülle; man spricht dann von relativ inneren Punkten.
Literatur
- Boto von Querenburg: Mengentheoretische Topologie. 3. neu bearbeitete und erweiterte Auflage. Springer-Verlag, Berlin u. a. 2001, ISBN 3-540-67790-9 (Springer-Lehrbuch).


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 11.12. 2021