
Komplement (Mengenlehre)
In der Mengentheorie und anderen Teilgebieten der Mathematik sind zwei verschiedene Komplemente definiert: Das relative Komplement und das absolute Komplement.
Relatives Komplement
Definition
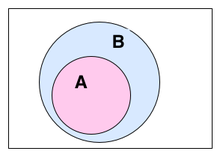
Sind
und
Mengen, dann ist das relative Komplement, auch mengentheoretisches
Komplement oder mengentheoretische Differenz genannt, die Menge genau
der Elemente aus
,
welche nicht in
enthalten sind. Die formale Definition des relativen Komplements ist
und man sagt „
ohne
“
oder „relatives Komplement von
in
“.
Das Komplement entspricht also der Subtraktion
von Mengen. „Relativ“ heißt es deshalb, weil das Komplement einer Menge
stets in Relation zu einer weiteren Menge
angegeben wird.
Das relative Komplement kann auch so definiert werden, dass
eine Teilmenge von
sein soll. Grund hierfür ist, dass für die Definition des Komplements nur
diejenigen Elemente in
von Relevanz sind, die gleichzeitig auch Elemente in
sind. Die Definitionen sind insofern äquivalent, als dass für beliebige Mengen
und
stets
gilt, d. h. es gibt mit
eine Teilmenge von
,
deren Komplement in
dem Komplement von
(welches nicht notwendigerweise Teilmenge von
ist) in
entspricht.
Beispiele
- Für
(reelle Zahlen) und
(rationale Zahlen), ist
die Menge der irrationalen Zahlen.
Eigenschaften
Im Folgenden sind einige Eigenschaften relativer Komplemente im Zusammenhang
mit den mengentheoretischen Operationen Vereinigung und Durchschnitt
aufgelistet. Seien ,
und
Mengen, dann gelten folgende Identitäten:
Absolutes Komplement
Definition
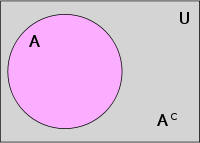
Ist ein Universum
definiert, so wird für jede Menge
das relative Komplement von
in
auch absolutes Komplement (oder einfach Komplement) von
genannt und als
(manchmal auch als
,
oder auch als
,
bzw.
wenn
fest ist) notiert, es ist also:
Beispiel
Ist das Universum zum Beispiel die Menge der natürlichen Zahlen, so ist das (absolute) Komplement der Menge der geraden Zahlen die Menge der ungeraden Zahlen.
In der Wahrscheinlichkeitsrechnung
ist häufig der Ergebnisraum
als Universum gesetzt. Für ein Ereignis
ist dessen Gegenereignis
das Komplement von
.
Zum Beispiel ist das Komplement des Ereignisses „Würfel zeigt eine 5 oder 6“ das
Ereignis „Würfel zeigt eine Zahl kleiner/gleich 4“.
Eigenschaften
Im Folgenden sind einige Eigenschaften absoluter Komplemente im Zusammenhang
mit den mengentheoretischen Operationen Vereinigung und Durchschnitt
aufgelistet. Seien
und
Teilmengen des Universums
dann gelten folgende Identitäten:
Komplementgesetze:
- Ist
, so ist
Involution:
Beziehungen zwischen relativen und absoluten Komplementen:
Die ersten beiden Komplementgesetze zeigen, dass, wenn
eine echte nichtleere Teilmenge von
ist,
eine Partition
von
ist.
Siehe auch
Literatur
- Oliver Deiser: Einführung in die Mengenlehre. Die Mengenlehre Georg Cantors und ihre Axiomatisierung durch Ernst Zermelo. 2., verbesserte und erweiterte Auflage. Springer, Berlin u. a. 2004, ISBN 3-540-20401-6.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 10.02. 2022