Wahrscheinlichkeitstheorie

Die Wahrscheinlichkeitstheorie oder Wahrscheinlichkeitsrechnung ist ein Teilgebiet der Mathematik, das aus der Formalisierung der Modellierung und der Untersuchung von Zufallsgeschehen hervorgegangen ist. Gemeinsam mit der mathematischen Statistik, die anhand von Beobachtungen zufälliger Vorgänge Aussagen über das zugrunde liegende Modell trifft, bildet sie das mathematische Teilgebiet der Stochastik. Die zentralen Objekte der Wahrscheinlichkeitstheorie sind zufällige Ereignisse, Zufallsvariablen und stochastische Prozesse.

Axiomatischer Aufbau

Wie jedes Teilgebiet der modernen Mathematik wird auch die Wahrscheinlichkeitstheorie mengentheoretisch formuliert und auf axiomatischen Vorgaben aufgebaut. Ausgangspunkt der Wahrscheinlichkeitstheorie sind Ereignisse, die als Mengen aufgefasst werden und denen Wahrscheinlichkeiten zugeordnet sind; Wahrscheinlichkeiten sind reelle Zahlen zwischen 0 und 1; die Zuordnung von Wahrscheinlichkeiten zu Ereignissen muss gewissen Mindestanforderungen genügen.

Diese Definitionen geben keinen Hinweis darauf, wie man die Wahrscheinlichkeiten einzelner Ereignisse ermitteln kann; sie sagen auch nichts darüber aus, was Zufall und was Wahrscheinlichkeit eigentlich sind. Die mathematische Formulierung der Wahrscheinlichkeitstheorie ist somit für verschiedene Interpretationen offen, ihre Ergebnisse sind dennoch exakt und vom jeweiligen Verständnis des Wahrscheinlichkeitsbegriffs unabhängig.

Definitionen

Konzeptionell wird als Grundlage der mathematischen Betrachtung von einem Zufallsvorgang oder Zufallsexperiment ausgegangen. Alle möglichen Ergebnisse dieses Zufallsvorgangs fasst man in der Ergebnismenge $\Omega$ zusammen. Häufig interessiert man sich jedoch gar nicht für das genaue Ergebnis $\omega \in \Omega$ , sondern nur dafür, ob es in einer bestimmten Teilmenge der Ergebnismenge liegt was so interpretiert werden kann, dass ein Ereignis eingetreten ist oder nicht. Ein Ereignis ist also als eine Teilmenge von $\Omega$ definiert. Enthält das Ereignis genau ein Element der Ergebnismenge, handelt es sich um ein Elementarereignis. Zusammengesetzte Ereignisse enthalten mehrere Ergebnisse. Das Ergebnis ist also ein Element der Ergebnismenge, das Ereignis jedoch eine Teilmenge.

Damit man den Ereignissen in sinnvoller Weise Wahrscheinlichkeiten zuordnen kann, werden sie in einem Mengensystem aufgeführt, der Ereignisalgebra oder dem Ereignissystem $\Sigma$ über $\Omega$ , einer Menge von Teilmengen von $\Omega$ , für die gilt: Sie enthält $\Omega$ und ist ein σ-Körper, d.h., sie ist gegenüber den Mengenoperationen der Vereinigung und der Komplementbildung (relativ bzgl. $\Omega$ ) abgeschlossen genauso wie gegenüber der unendlichen Vereinigung abzählbar vieler Mengen. Die Wahrscheinlichkeiten sind dann Bilder einer gewissen Abbildung des Ereignisraums in das Intervall [0,1]. Solch eine Abbildung heißt Wahrscheinlichkeitsmaß. Das Tripel $(\Omega,\Sigma,P)$ wird als Wahrscheinlichkeitsraum bezeichnet.

Axiome von Kolmogorow

Die axiomatische Begründung der Wahrscheinlichkeitstheorie wurde in den 1930er Jahren von Andrei Nikolajewitsch Kolmogorow entwickelt. Ein Wahrscheinlichkeitsmaß muss demnach folgende drei Axiome erfüllen:

Axiome:

Für jedes Ereignis $A\in\Sigma$ ist die Wahrscheinlichkeit von eine reelle Zahl zwischen 0 und 1: $0\leq P(A)\leq 1$ .
Das sichere Ereignis $\Omega\in\Sigma$ hat die Wahrscheinlichkeit 1: $P(\Omega )=1$ .
Die Wahrscheinlichkeit einer Vereinigung abzählbar vieler inkompatibler Ereignisse ist gleich der Summe der Wahrscheinlichkeiten der einzelnen Ereignisse. Dabei heißen Ereignisse $A_{i}$ inkompatibel, wenn sie paarweise disjunkt sind, also bei $A_i \cap A_j = \emptyset$ für alle $i\neq j$ . Es gilt daher $P\left(A_1\dot\cup A_2\dot\cup\cdots\right) = \sum P(A_i)$ . Diese Eigenschaft wird auch σ-Additivität genannt.

Beispiel: Im Rahmen einer physikalischen Modellbildung wird ein Wahrscheinlichkeitsmaß zur Beschreibung des Ergebnisses eines Münzwurfes angesetzt, die möglichen Ergebnisse (Ereignisse genannt) mögen Zahl und Kopf lauten.

Dann ist die Ergebnismenge $\Omega=\{\text{Zahl}, \text{Kopf}\}$ .
Als Ereignisraum kann die Potenzmenge ${\mathcal {P}}(\Omega )\;$ gewählt werden, also $\Sigma=\{\emptyset,\{\text{Zahl}\},\{\text{Kopf}\},\Omega\}$ .
Für das Wahrscheinlichkeitsmaß steht aufgrund der Axiome fest:
- $P(\emptyset )=0$
- $P(\{\text{Zahl}\})=1-P(\{\text{Kopf}\})$
- $P(\Omega )=1$

Zusätzliche physikalische Annahmen über die Beschaffenheit der Münze können nun etwa zur Wahl $P(\{\text{Kopf}\})=P(\{\text{Zahl}\})=0{,}5$ führen.

Folgerungen

Aus den Axiomen ergeben sich unmittelbar einige Folgerungen:

1. Aus der Additivität der Wahrscheinlichkeit disjunkter Ereignisse folgt, dass komplementäre Ereignisse (Gegenereignisse) komplementäre Wahrscheinlichkeiten (Gegenwahrscheinlichkeiten) haben: $P(\Omega\setminus A) = 1-P(A)$ .

Beweis: Es ist $(\Omega\setminus A)\cup A = \Omega$ sowie $(\Omega\setminus A) \cap A = \emptyset$ . Folglich nach Axiom (3): $P(\Omega \setminus A) + P(A) = P(\Omega)$ und dann nach Axiom (2): $P(\Omega \setminus A) + P(A) = 1$ . Umgestellt ergibt sich: $P(\Omega \setminus A) = 1 - P(A)$ .

2. Daraus folgt, dass das unmögliche Ereignis, die leere Menge, die Wahrscheinlichkeit Null hat: $P(\emptyset )=0$ .

Beweis: Es ist $\emptyset\cup\Omega = \Omega$ und $\emptyset\cap\Omega = \emptyset$ , also nach Axiom (3): $P(\emptyset) + P(\Omega) = P(\Omega)$ . Hieraus folgt $P(\emptyset) = 0$ .

3. Für die Vereinigung nicht notwendig disjunkter Ereignisse folgt: $P(A \cup B) = P(A) + P(B) - P(A \cap B)$ .

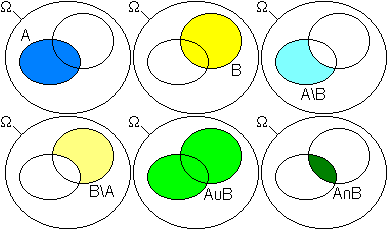
Beweis: Die für den Beweis erforderlichen Mengen sind im obigen Bild dargestellt. Die Menge $A\cup B$ kann danach als Vereinigung von drei disjunkten Mengen dargestellt werden:

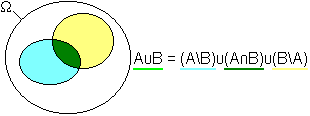
Hieraus folgt nach (3): $P(A \cup B) = P(A \setminus B) + P(A \cap B) + P(B \setminus A)$ .

Andererseits ist nach (3) sowohl

$P(A) = P(A \setminus B) + P(A \cap B)$ als auch

$P(B) = P(A \cap B) + P(B \setminus A)$ .

Addition liefert:

$P(A)+P(B)=P(A\setminus B)+P(A\cap B)+P(A\cap B)+P(B\setminus A)=P(A \cup B)+P(A\cap B)$ .

Umstellen ergibt $P(A \cup B) = P(A) + P(B) - P(A \cap B)$ .

Die Siebformel von Poincaré-Sylvester verallgemeinert diese Behauptung im Falle n verschiedener (nicht notwendig disjunkter) Teilmengen.

Im Weiteren ist zwischen abzählbaren und überabzählbaren Ergebnismengen zu unterscheiden.

Abzählbare Ergebnismenge

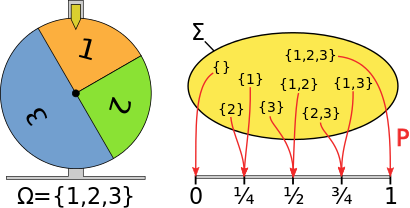
Beispiel: Ein Glücksrad mit Ergebnismenge $\Omega=\{1,2,3\}$ , Ereignisraum $\Sigma$ (hier die Potenzmenge von $\Omega$ ) und Wahrscheinlichkeitsmaß .

Bei einer abzählbaren Ergebnismenge kann jedem Elementarereignis eine positive Wahrscheinlichkeit zugewiesen werden. Wenn $\Omega$ endlich oder abzählbar unendlich ist, kann man für die σ-Algebra $\Sigma$ die Potenzmenge von $\Omega$ wählen. Die Summe der Wahrscheinlichkeiten aller Elementarereignisse aus $\Omega$ ist hier 1.

Überabzählbare Ergebnismenge

Die Wahrscheinlichkeit, mit einer als punktförmig angenommenen Dartspitze einen bestimmten Punkt auf einer Scheibe zu treffen, ist null. Eine sinnvolle mathematische Theorie kann man nur auf der Wahrscheinlichkeit aufbauen, bestimmte Teilflächen zu treffen. Solche Wahrscheinlichkeiten lassen sich durch eine Wahrscheinlichkeitsdichte beschreiben.

Ein Prototyp einer überabzählbaren Ergebnismenge ist die Menge der reellen Zahlen. In vielen Modellen ist es nicht möglich, allen Teilmengen der reellen Zahlen sinnvoll eine Wahrscheinlichkeit zuzuordnen. Als Ereignissystem wählt man statt der Potenzmenge der reellen Zahlen hier meist die Borelsche σ-Algebra, das ist die kleinste σ-Algebra, die alle Intervalle von reellen Zahlen als Elemente enthält. Die Elemente dieser σ-Algebra nennt man Borelsche Mengen oder auch (Borel)-messbar. Wenn die Wahrscheinlichkeit P(A) jeder Borelschen Menge als Integral

$P(A)=\int_A f(x)\,\mathrm{d}x$

über eine Wahrscheinlichkeitsdichte geschrieben werden kann, wird absolut stetig genannt. In diesem Fall (aber nicht nur in diesem) haben alle Elementarereignisse {x} die Wahrscheinlichkeit 0. Die Wahrscheinlichkeitsdichte eines absolut stetigen Wahrscheinlichkeitsmaßes ist nur fast überall eindeutig bestimmt, d.h., sie kann auf einer beliebigen Lebesgue-Nullmenge, also einer Menge vom Lebesgue-Maß 0, abgeändert werden, ohne dass verändert wird. Wenn die erste Ableitung der Verteilungsfunktion von existiert, so ist sie eine Wahrscheinlichkeitsdichte von P. Die Werte der Wahrscheinlichkeitsdichte werden jedoch nicht als Wahrscheinlichkeiten interpretiert.

Spezielle Eigenschaften im Fall diskreter Wahrscheinlichkeitsräume

Laplace-Experimente

Wenn man annimmt, dass nur endlich viele Elementarereignisse möglich und alle gleichberechtigt sind, d.h. mit der gleichen Wahrscheinlichkeit eintreten (wie zum Beispiel beim Werfen einer idealen Münze, wobei {Zahl} und {Kopf} jeweils die Wahrscheinlichkeit 0,5 besitzen), so spricht man von einem Laplace-Experiment. Dann lassen sich Wahrscheinlichkeiten einfach berechnen: Wir nehmen eine endliche Ergebnismenge $\Omega$ an, die die Mächtigkeit $|\Omega|=n$ besitzt, d.h., sie hat Elemente. Dann ist die Wahrscheinlichkeit jedes Elementarereignisses einfach $P=\tfrac 1 n$ .

Beweis: Wenn $|\Omega|=n$ ist, dann gibt es Elementarereignisse $E_1, \ldots, E_n$ . Es ist dann einerseits $\Omega = E_1 \cup \cdots \cup E_n$ und andererseits sind je zwei Elementarereignisse disjunkt (inkompatibel: wenn das eine eintritt, kann das andere nicht eintreten). Also sind die Voraussetzungen für Axiom (3) erfüllt, und es gilt:

$P(E_1) + \cdots + P(E_n) = P(\Omega) = 1.$

Da nun andererseits $P(E_1) = \cdots = P(E_n) = P$ sein soll, ist $n \cdot P = 1$ und daher umgestellt: $P = \tfrac 1 n$ , wie behauptet.

Als Konsequenz folgt, dass für Ereignisse, die sich aus mehreren Elementarereignissen zusammensetzen, die entsprechend vielfache Wahrscheinlichkeit gilt. Ist ein Ereignis der Mächtigkeit |A| = m , so ist die Vereinigung von Elementarereignissen. Jedes davon hat die Wahrscheinlichkeit $P = \tfrac 1 n$ , also ist $P(A) = m \cdot \tfrac 1 n = \tfrac m n$ . Man erhält also den einfachen Zusammenhang

$P(A) = \frac{|A|}{|\Omega|}.$

Bei Laplace-Versuchen ist die Wahrscheinlichkeit eines Ereignisses gleich der Zahl der für dieses Ereignis günstigen Ergebnisse, dividiert durch die Zahl der insgesamt möglichen Ergebnisse.

Nachstehend ein Beispiel beim Würfeln mit einem idealen Würfel.

$\Omega =\{$ ⚀⚁⚂⚃⚄⚅ $\}$

$H=\{$ ⚄⚅ $\}$

$P(H)={\frac {|H|}{|\Omega |}}={\frac {2}{6}}={\frac {1}{3}}$

Das Ereignis = Hohe Augenzahl (5 oder 6) hat die Wahrscheinlichkeit 1/3.

Ein typischer Laplace-Versuch ist auch das Ziehen einer Karte aus einem Spiel mit Karten oder das Ziehen einer Kugel aus einer Urne mit Kugeln. Hier hat jedes Elementarereignis die gleiche Wahrscheinlichkeit. Um die Anzahl der Elementarereignisse bei Laplace-Versuchen zu bestimmen, werden häufig Methoden der Kombinatorik verwendet.

Das Konzept der Laplace-Experimente lässt sich auf den Fall einer stetigen Gleichverteilung verallgemeinern.

Bedingte Wahrscheinlichkeit

Unter einer bedingten Wahrscheinlichkeit versteht man die Wahrscheinlichkeit für das Eintreten eines Ereignisses unter der Voraussetzung, dass das Eintreten eines anderen Ereignisses bereits bekannt ist. Natürlich muss eintreten können, es darf also nicht das unmögliche Ereignis sein. Man schreibt dann P(A|B) oder seltener P_B (A) für „Wahrscheinlichkeit von unter der Voraussetzung “, kurz „ von , vorausgesetzt “.

Beispiel: Die Wahrscheinlichkeit, aus einem Skatblatt eine Herz-Karte zu ziehen (Ereignis ), beträgt 1/4, denn es gibt 32 Karten und darunter 8 Herz-Karten. Dann ist $P(\text{Herz}) = \tfrac 8{32} = \tfrac 1 4$ . Das Gegenereignis ist dann Karo, Pik oder Kreuz und hat deshalb die Wahrscheinlichkeit $\tfrac{24}{32} = \tfrac 3 4$ .

Ergebnismenge beim Ziehen einer Karte aus einem Skatspiel

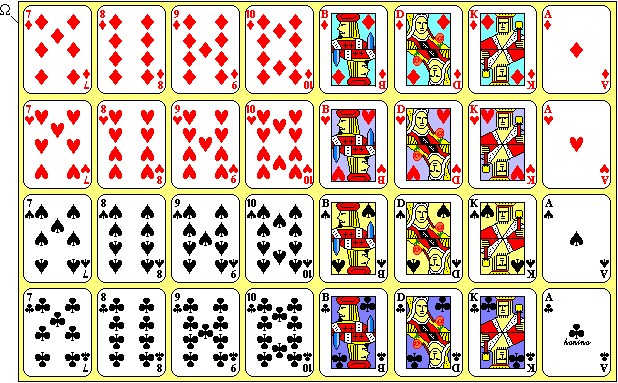
Wenn nun aber bereits das Ereignis „Die Karte ist rot“ eingetreten ist (es wurde eine Herz- oder Karo-Karte gezogen, es ist aber nicht bekannt, welche der beiden Farben), man also nur noch die Auswahl unter den 16 roten Karten hat, dann ist $P(A|B) = \tfrac 8{16} = \tfrac 1 2$ die Wahrscheinlichkeit, dass es sich dann um das Herz-Blatt handelt.

Diese Überlegung galt für einen Laplaceversuch. Für den allgemeinen Fall definiert man die bedingte Wahrscheinlichkeit von „, vorausgesetzt “ als

$P(A \vert B) = \frac{P(A \cap B)}{P(B)}.$

Dass diese Definition sinnvoll ist, zeigt sich daran, dass die so definierte Wahrscheinlichkeit den Axiomen von Kolmogorow genügt, wenn man sich auf als neue Ergebnismenge beschränkt; d.h., dass gilt:

$0 \le P(A \vert B) \le 1$
$P(B \vert B)=1$
Wenn $A_1,\ldots,A_k$ paarweise disjunkt sind, so ist $P(A_1 \cup \cdots \cup A_k \vert B) = P(A_1 \vert B) + \cdots + P(A_k \vert B)$

Beweis:

$P(A \vert B)$ ist Quotient zweier Wahrscheinlichkeiten, für welche nach Axiom (1) gilt $P(A \cap B) \ge 0$ und $P(B) \ge 0$ . Da nicht das unmögliche Ereignis sein soll, ist sogar . Also gilt auch für den Quotienten $P(A \vert B) \ge 0$ . Ferner sind $A\cap B$ und $B\setminus A$ disjunkt, und ihre Vereinigung ist . Also ist nach Axiom (3): $P(A \cap B) = P(B) - P(B \setminus A)$ .
Da $P(B \setminus A) \ge 0$ ist, folgt $P(A \cap B) \le P(B)$ und daher $P(A \vert B) \le 1$ .
Es ist $P(B \vert B) = \frac{P(B \cap B)}{P(B)} = \frac{P(B)}{P(B)} = 1.$
Des Weiteren ergibt sich:

${\begin{aligned}P(A_{1}\cup \cdots \cup A_{k}\vert B)&={\frac {P((A_{1}\cup \cdots \cup A_{k})\cap B)}{P(B)}}\\&={\frac {P((A_{1}\cap B)\cup \cdots \cup (A_{k}\cap B))}{P(B)}}\\&={\frac {P(A_{1}\cap B)+\cdots +P(A_{k}\cap B)}{P(B)}}\\&={\frac {P(A_{1}\cap B)}{P(B)}}+\cdots +{\frac {P(A_{k}\cap B)}{P(B)}}\\\\&=P(A_{1}\vert B)+\cdots +P(A_{k}\vert B).\end{aligned}}$

Dies war zu zeigen.

Beispiel: Es sei wie oben das Ereignis „Ziehen einer Herz-Karte“ und das Ereignis „Es ist eine rote Karte“. Dann ist:

$P(A \cap B) = \frac 8{32} = \frac 1 4$

und

$P(B)= \frac{16}{32} = \frac 1 2.$

Folglich gilt:

$P(A \vert B) = \frac{P(A \cap B)}{P(B)} = \frac{\frac 1 4}{\frac 1 2} = \frac 1 2.$

Aus der Definition der bedingten Wahrscheinlichkeit ergeben sich folgende Konsequenzen:

Verbundwahrscheinlichkeit (Schnittmengen von Ereignissen)

Das gleichzeitige Eintreten zweier Ereignisse und entspricht mengentheoretisch dem Eintreten des Verbund-Ereignisses $A\cap B$ . Die Wahrscheinlichkeit hiervon berechnet sich zur gemeinsamen Wahrscheinlichkeit oder Verbundwahrscheinlichkeit

$P(A \cap B) = P(A) \cdot P(B \vert A) = P(B) \cdot P(A \vert B).$

Beweis: Nach Definition der bedingten Wahrscheinlichkeit ist einerseits

$P(A \vert B) = \frac{P(A\cap B)}{P(B)}$

und andererseits auch

$P(B \vert A) = \frac{P(A \cap B)}{P(A)}.$

Umstellen nach $P(A \cap B)$ liefert dann sofort die Behauptung.

Beispiel: Es wird eine Karte aus 32 Karten gezogen. sei das Ereignis: „Es ist ein König“. sei das Ereignis: „Es ist eine Herz-Karte“. Dann ist $A\cap B$ das gleichzeitige Eintreten von und , also das Ereignis: „Die gezogene Karte ist ein Herz-König“. Offenbar ist $P(A) = \tfrac 4{32} = \tfrac 1 8$ . Ferner ist $P(B|A) = \tfrac 1 4$ , denn es gibt nur eine Herz-Karte unter den vier Königen. Und in der Tat ist dann $P(A \cap B) = P(A) \cdot P(B\vert A) = \tfrac 1 8 \cdot \tfrac 1 4 = \tfrac 1{32}$ die Wahrscheinlichkeit für den Herz-König.

Satz von Bayes

Die bedingte Wahrscheinlichkeit von unter der Bedingung lässt sich durch die bedingte Wahrscheinlichkeit von unter der Bedingung durch

$P(A \mid B)=\frac{P(B\mid A)\cdot P(A)}{P(B)}$

ausdrücken, wenn man die totalen Wahrscheinlichkeiten P(B) und P(A) kennt (Satz von Bayes).

Abhängigkeit und Unabhängigkeit von Ereignissen

Ereignisse nennt man unabhängig voneinander, wenn das Eintreten des einen die Wahrscheinlichkeit des anderen nicht beeinflusst. Im umgekehrten Fall nennt man sie abhängig. Man definiert:

Zwei Ereignisse und sind unabhängig, wenn $P(A \cap B) = P(A) \cdot P(B)$ gilt.

Ungenau, aber einprägsam formuliert: Bei unabhängigen Ereignissen kann man die Wahrscheinlichkeiten multiplizieren.

Dass dies dem Begriff „Unabhängigkeit“ gerecht wird, erkennt man durch Umstellen nach P(A) :

$P(A) = \frac{P(A \cap B)}{P(B)} = P(A \vert B).$

Das bedeutet: Die totale Wahrscheinlichkeit für ist ebenso groß wie die Wahrscheinlichkeit für , vorausgesetzt ; das Eintreten von beeinflusst also die Wahrscheinlichkeit von nicht.

Beispiel: Es wird eine aus 32 Karten gezogen. sei das Ereignis „Es ist eine Herz-Karte“. sei das Ereignis „Es ist eine Bild-Karte“. Diese Ereignisse sind unabhängig, denn das Wissen, dass man eine Bild-Karte zieht, beeinflusst nicht die Wahrscheinlichkeit, dass es eine Herz-Karte ist (Der Anteil der Herz-Karten unter den Bilder-Karten ist ebenso groß wie der Anteil der Herz-Karten an allen Karten). Offenbar ist $P(A) = \tfrac 8{32} = \tfrac 1 4$ und $P(B) = \tfrac{12}{32} = \tfrac 3 8$ . $A\cap B$ ist das Ereignis „Es ist eine Herz-Bildkarte“. Da es davon drei gibt, ist $P(A \cap B) = \tfrac 3{32}$ . Und in der Tat stellt man fest, dass $\tfrac 1 4 \cdot \tfrac 3 8 = \tfrac 3{32}$ ist.

Maßtheoretische Sichtweise

Die klassische Wahrscheinlichkeitsrechnung betrachtet nur Wahrscheinlichkeiten auf diskreten Wahrscheinlichkeitsräumen und stetige Modelle mit Dichtefunktionen. Diese beiden Ansätze lassen sich durch die moderne Formulierung der Wahrscheinlichkeitstheorie, die auf den Konzepten und Ergebnissen der Maß- und Integrationstheorie beruht, vereinheitlichen und verallgemeinern.

Wahrscheinlichkeitsräume

→ Hauptartikel: Wahrscheinlichkeitsraum

In dieser Sichtweise ist ein Wahrscheinlichkeitsraum $(\Omega ,\Sigma ,P)$ ein Maßraum mit einem Wahrscheinlichkeitsmaß . Das bedeutet, die Ergebnismenge $\Omega$ ist eine beliebige Menge, der Ereignisraum $\Sigma$ ist eine σ-Algebra mit Grundmenge $\Omega$ und $P \colon \Sigma \to [0,1]$ ist ein Maß, das durch $P(\Omega )=1$ normiert ist.

Wichtige Standardfälle von Wahrscheinlichkeitsräumen sind:

$\Omega$ ist eine abzählbare Menge und $\Sigma$ ist die Potenzmenge von $\Omega$ . Dann ist jedes Wahrscheinlichkeitsmaß eindeutig festgelegt durch seine Werte $P(\{\omega\})$ auf den einelementigen Teilmengen von $\Omega$ und für alle $A \in \Sigma$ gilt

$P(A) = \sum_{\omega\in A} P(\{\omega\})$ .

$\Omega$ ist eine Teilmenge von $\mathbb {R} ^{n}$ und $\Sigma$ ist die Borelsche σ-Algebra auf $\Omega$ . Ist das Wahrscheinlichkeitsmaß absolut stetig bezüglich des Lebesgue-Maßes, dann besitzt nach dem Satz von Radon-Nikodým eine Lebesgue-Dichte , d.h., für alle $A \in \Sigma$ gilt

$P(A) = \int_A f(x) \, \mathrm d x$ .

Umgekehrt wird für eine nichtnegative messbare Funktion , welche die Normierungsbedingung $\textstyle \int_\Omega f(x) \, dx = 1$ erfüllt, durch diese Formel ein Wahrscheinlichkeitsmaß auf $\Omega$ definiert.

$\textstyle\Omega = \prod_{i\in I} \Omega_i$ ist ein kartesisches Produkt und $\textstyle\Sigma = \bigotimes_{i\in I} \Sigma_i$ ist die Produkt-σ-Algebra von σ-Algebren $\Sigma_i$ auf $\Omega _{i}$ . Sind Wahrscheinlichkeitsmaße $P_{i}$ auf $\Omega _{i}$ gegeben, dann wird durch das Produktmaß $\textstyle P = \bigotimes_{i\in I} P_i$ ein Wahrscheinlichkeitsmaß auf $\Omega$ definiert, das die unabhängige Hintereinanderausführung der Einzelexperimente $(\Omega_i, \Sigma_i, P_i)_{i\in I}$ modelliert.

Zufallsvariable

→ Hauptartikel: Zufallsvariable

Eine Zufallsvariable ist das mathematische Konzept für eine Größe, deren Wert vom Zufall abhängig ist. Aus maßtheoretischer Sicht handelt es sich um eine messbare Funktion auf einem Wahrscheinlichkeitsraum $(\Omega ,\Sigma ,P)$ in einen Messraum $(\Omega', \Sigma')$ bestehend aus einer Menge $\Omega '$ und einer σ-Algebra $\Sigma'$ auf $\Omega '$ . Messbarkeit bedeutet dabei, dass für alle $A' \in \Sigma'$ das Urbild $X^{-1}(A')$ ein Element der σ-Algebra $\Sigma$ ist. Die Verteilung von ist dann nichts anderes als das Bildmaß

$P_X := P \circ X^{-1} : \Sigma' \to [0,1], \quad P \circ X^{-1}(A') = P(X^{-1}(A'))$ ,

das von auf dem Messraum $(\Omega', \Sigma')$ induziert wird und diesen zu einem Wahrscheinlichkeitsraum $(\Omega', \Sigma', P_X)$ macht.

Der Erwartungswert einer reellwertigen Zufallsvariable mittelt die möglichen Ergebnisse. Er lässt sich abstrakt definieren als Integral von bezüglich des Wahrscheinlichkeitsmaßes :

$\operatorname {E} (X)=\int _{\Omega }X\,\mathrm {d} P$ .

Wahrscheinlichkeitstheorie und Statistik

Wahrscheinlichkeitstheorie und mathematische Statistik werden zusammenfassend auch als Stochastik bezeichnet. Beide Gebiete stehen in enger wechselseitiger Beziehung:

Statistische Verteilungen werden regelmäßig unter der Annahme modelliert, dass sie das Resultat zufälliger Prozesse sind.
Statistische Verfahren können auf numerische Weise Anhaltspunkte für das Verhalten von Wahrscheinlichkeitsverteilungen liefern.

Anwendungsgebiete

Die Wahrscheinlichkeitstheorie entstand aus dem Problem der gerechten Verteilung des Einsatzes bei abgebrochenen Glücksspielen. Auch andere frühe Anwendungen stammen aus dem Bereich des Glücksspiels.

Heute ist die Wahrscheinlichkeitstheorie eine Grundlage der mathematischen Statistik. Die angewandte Statistik nutzt Ergebnisse der Wahrscheinlichkeitstheorie, um Umfrageergebnisse zu analysieren oder Wirtschaftsprognosen zu erstellen.

Große Bereiche der Physik wie die Thermodynamik und die Quantenmechanik nutzen die Wahrscheinlichkeitstheorie zur theoretischen Beschreibung ihrer Resultate.

Sie ist ferner die Grundlage für mathematische Disziplinen wie die Zuverlässigkeitstheorie, die Erneuerungstheorie und die Warteschlangentheorie und das Werkzeug zur Analyse in diesen Bereichen.

Auch in der Mustererkennung ist die Wahrscheinlichkeitstheorie von zentraler Bedeutung.

Siehe auch

Basierend auf einem Artikel in:

Wikipedia.de