Satz von Bayes

Illustration des Satzes von Bayes durch Überlagerung der beiden ihm zugrundeliegenden Entscheidungsbäume bzw. Baumdiagramme

Der Satz von Bayes ist ein mathematischer Satz aus der Wahrscheinlichkeitstheorie, der die Berechnung bedingter Wahrscheinlichkeiten beschreibt. Er ist nach dem englischen Mathematiker Thomas Bayes benannt, der ihn erstmals in einem Spezialfall in der 1763 posthum veröffentlichten Abhandlung An Essay Towards Solving a Problem in the Doctrine of Chances beschrieb. Er wird auch Formel von Bayes oder (als Lehnübersetzung) Bayes-Theorem genannt.

Formel

Für zwei Ereignisse und mit P(B) > 0 lässt sich die Wahrscheinlichkeit von unter der Bedingung, dass eingetreten ist, durch die Wahrscheinlichkeit von unter der Bedingung, dass eingetreten ist, errechnen:

$P(A\mid B) \; = \; \frac {P(B\mid A) \cdot P(A)} {P(B)}$ .

Hierbei ist

$P(A\mid B)$ die (bedingte) Wahrscheinlichkeit des Ereignisses unter der Bedingung, dass eingetreten ist,

$P(B\mid A)$ die (bedingte) Wahrscheinlichkeit des Ereignisses unter der Bedingung, dass eingetreten ist,

die A-priori-Wahrscheinlichkeit des Ereignisses und

die A-priori-Wahrscheinlichkeit des Ereignisses .

Bei endlich vielen Ereignissen lautet der Satz von Bayes:

Wenn $A_{i},\; i = 1, \dotsc, N$ eine Zerlegung der Ergebnismenge in disjunkte Ereignisse ist, gilt für die A-posteriori-Wahrscheinlichkeit $P(A_i \mid B)$

$P(A_i \mid B) \; = \; \frac{P(B\mid A_i) \cdot P(A_i)}{P(B)} \; = \; \frac{P\left(B\mid A_i\right)\cdot P(A_i)}{\sum_{j=1} ^{N} P\left(B\mid A_j\right) \cdot P(A_j)}$ .

Den letzten Umformungsschritt bezeichnet man auch als Marginalisierung.

Da ein Ereignis und sein Komplement A^c stets eine Zerlegung der Ergebnismenge darstellen, gilt insbesondere

$P(A \mid B) \; = \; \frac{P(B \mid A) \cdot P(A)}{P(B \mid A) \cdot P(A) + P(B \mid A^c) \cdot P(A^c)}$ .

Des Weiteren gilt der Satz auch für eine Zerlegung des Grundraumes $\Omega$ in abzählbar viele paarweise disjunkte Ereignisse.

Beweis

Der Wahrscheinlichkeitsbaum illustriert $P\left(A\mid B\right) P(B) = P(A \cap B)$ .

Der Satz folgt unmittelbar aus der Definition der bedingten Wahrscheinlichkeit:

$P\left(A\mid B\right) \; = \; \frac{P(A \cap B)}{P(B)} \; = \; \frac{\frac{P(A\cap B)}{P(A)} \cdot P(A)}{P(B)} \; = \; \frac{P\left(B\mid A\right)\cdot P(A)}{P\left(B\right)}$ .

Die Beziehung

$P(B)\; = \; \sum_{j=1}^N P\left(A_j\cap B\right) \; = \; {\sum_{j=1}^{N} P\left(B\mid A_j\right)\cdot P\left(A_j\right)}$

ist eine Anwendung des Gesetzes der totalen Wahrscheinlichkeit.

Interpretation

Der Satz von Bayes erlaubt in gewissem Sinn das Umkehren von Schlussfolgerungen: Man geht von einem bekannten Wert $P(B \mid A)$ aus, ist aber eigentlich an dem Wert $P(A \mid B)$ interessiert. Beispielsweise ist es von Interesse, wie groß die Wahrscheinlichkeit ist, dass jemand eine bestimmte Krankheit hat, wenn ein dafür entwickelter Schnelltest ein positives Ergebnis zeigt. Aus empirischen Studien kennt man in der Regel die Wahrscheinlichkeit dafür, mit der der Test bei einer von dieser Krankheit befallenen Person zu einem positiven Ergebnis führt. Die gewünschte Umrechnung ist nur dann möglich, wenn man die Prävalenz der Krankheit kennt, das heißt die (absolute) Wahrscheinlichkeit, mit der die betreffende Krankheit in der Gesamtpopulation auftritt (siehe Rechenbeispiel 2).

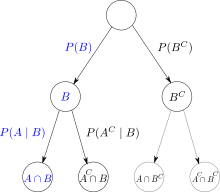
Für das Verständnis kann ein Entscheidungsbaum oder eine Vierfeldertafel helfen. Das Verfahren ist auch als Rückwärtsinduktion bekannt.

Mitunter begegnet man dem Fehlschluss, direkt von $P(B \mid A)$ auf $P(A \mid B)$ schließen zu wollen, ohne die A-priori-Wahrscheinlichkeit P(A) zu berücksichtigen, beispielsweise indem angenommen wird, die beiden bedingten Wahrscheinlichkeiten müssten ungefähr gleich groß sein. Wie der Satz von Bayes zeigt, ist das aber nur dann der Fall, wenn auch P(A) und P(B) ungefähr gleich groß sind.

Ebenso ist zu beachten, dass bedingte Wahrscheinlichkeiten für sich allein nicht dazu geeignet sind, eine bestimmte Kausalbeziehung nachzuweisen.

Anwendungsgebiete

Statistik: Alle Fragen des Lernens aus Erfahrung, bei denen eine A-priori-Wahrscheinlichkeitseinschätzung aufgrund von Erfahrungen verändert und in eine A-posteriori-Verteilung überführt wird (vgl. Bayessche Statistik).
Data-Mining: Bayes-Klassifikatoren sind theoretische Entscheidungsregeln mit beweisbar minimaler Fehlerrate.
Spamerkennung: Bayes-Filter – Von charakteristischen Wörtern in einer E-Mail (Ereignis A) wird auf die Eigenschaft Spam (Ereignis B) zu sein, geschlossen.
Künstliche Intelligenz: Hier wird der Satz von Bayes verwendet, um auch in Domänen mit „unsicherem“ Wissen Schlussfolgerungen ziehen zu können. Diese sind dann nicht deduktiv und somit auch nicht immer korrekt, sondern eher abduktiver Natur, haben sich aber zur Hypothesenbildung und zum Lernen in solchen Systemen als durchaus nützlich erwiesen.
Qualitätsmanagement: Beurteilung der Aussagekraft von Testreihen.
Entscheidungstheorie/Informationsökonomik: Bestimmung des erwarteten Wertes von zusätzlichen Informationen.
Grundmodell der Verkehrsverteilung.
Bioinformatik: Bestimmung funktioneller Ähnlichkeit von Sequenzen; Rekonstruktion von Stammbäumen und des Alters der Knoten
Kommunikationstheorie: Lösung von Detektions- und Dekodierproblemen.
Ökonometrie: Bayessche Ökonometrie

Rechenbeispiel 1

Urnenversuch

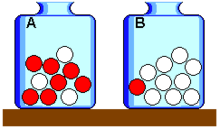
In den beiden Urnen und befinden sich jeweils zehn Kugeln. In sind sieben rote und drei weiße Kugeln, in eine rote und neun weiße. Es wird nun eine beliebige Kugel aus einer zufällig gewählten Urne gezogen. Anders ausgedrückt: Ob aus Urne oder gezogen wird, ist a priori gleich wahrscheinlich. Das Ergebnis der Ziehung ist: Die Kugel ist rot. Gesucht ist die Wahrscheinlichkeit, dass diese rote Kugel aus Urne stammt.

Es sei: das Ereignis „Die Kugel stammt aus Urne “,
das Ereignis „Die Kugel stammt aus Urne “ und
das Ereignis „Die Kugel ist rot“.

Dann gilt: $P(A) = P(B) = {1 \over 2}$ (beide Urnen sind a priori gleich wahrscheinlich)

$P(R \mid A) = {7 \over 10}$ (in Urne A sind 10 Kugeln, davon 7 rote)

$P(R \mid B) = {1 \over 10}$ (in Urne B sind 10 Kugeln, davon 1 rote)

$P(R) = P(R \mid A) \cdot P(A) + P(R \mid B) \cdot P(B) = {7 \over 10} \cdot {1 \over 2} + {1 \over 10} \cdot {1 \over 2} = {2 \over 5}$ (totale Wahrscheinlichkeit, eine rote Kugel zu ziehen)

Damit ist $P(A \mid R) = \frac {P(R \mid A) \cdot P(A)} {P(R)} = {{{7 \over 10} \cdot {1 \over 2}} \over {2 \over 5}} = { 7 \over 8 }$ .

Die bedingte Wahrscheinlichkeit, dass die gezogene rote Kugel aus der Urne gezogen wurde, beträgt also $\tfrac{7}{8} = 87{,}5\;\%$ .

Das Ergebnis der Bayes-Formel in diesem einfachen Beispiel kann leicht anschaulich eingesehen werden: Da beide Urnen a priori mit der gleichen Wahrscheinlichkeit ausgewählt werden und sich in beiden Urnen gleich viele Kugeln befinden, haben alle Kugeln – und damit auch alle acht roten Kugeln – die gleiche Wahrscheinlichkeit, gezogen zu werden. Wenn man wiederholt eine Kugel aus einer zufälligen Urne zieht und wieder in die richtige Urne zurücklegt, wird man im Durchschnitt in acht von 20 Fällen eine rote und in zwölf von 20 Fällen eine weiße Kugel ziehen (deshalb ist auch die totale Wahrscheinlichkeit, eine rote Kugel zu ziehen, gleich $\tfrac{8}{20} = \tfrac{2}{5}$ ). Von diesen acht roten Kugeln kommen im Mittel sieben aus Urne und eine aus Urne . Die Wahrscheinlichkeit, dass eine gezogene rote Kugel aus Urne stammt, ist daher gleich $\tfrac{7}{8}$ .

Rechenbeispiel 2

Eine bestimmte Krankheit tritt mit einer Prävalenz von 20 pro 100 000 Personen auf. Der Sachverhalt , dass ein Mensch diese Krankheit in sich trägt, hat also die Wahrscheinlichkeit P(K) = 0{,}0002 .

Ist ein Screening der Gesamtbevölkerung ohne Rücksicht auf Risikofaktoren oder Symptome geeignet, Träger dieser Krankheit zu ermitteln? Es würden dabei weit überwiegend Personen aus dem Komplement K^c von getestet, also Personen, die diese Krankheit nicht in sich tragen: Die Wahrscheinlichkeit, dass eine zu testende Person nicht Träger der Krankheit ist, beträgt $P(K^{c})=1-P(K)=0{,}9998$ .

bezeichne die Tatsache, dass der Test bei einer Person „positiv“ ausgefallen ist, also die Krankheit anzeigt. Es sei bekannt, dass der Test mit 95 % Wahrscheinlichkeit anzeigt (Sensitivität $= P(T\mid K) = 0{,}95$ ), aber manchmal auch bei Gesunden anspricht, d.h. ein falsch positives Testergebnis liefert, und zwar mit einer Wahrscheinlichkeit von $P(T\mid K^{c})=1\,\%$ (Spezifität $= 1 - P(T\mid K^c) = 1 - 0{,}01 = 0{,}99$ ).

Nicht nur für die Eingangsfrage, sondern in jedem Einzelfall , insbesondere vor dem Ergebnis weiterer Untersuchungen, interessiert die positiver prädiktiver Wert genannte bedingte Wahrscheinlichkeit $P(K\mid T)$ , dass positiv Getestete Träger der Krankheit sind.

Berechnung mit dem Satz von Bayes

$P(K\mid T) = \frac{P(T\mid K)P(K)}{P(T\mid K)P(K) + P(T\mid K^c)P(K^c)}=\frac{0{,}95 \cdot 0{,}0002}{0{,}95 \cdot 0{,}0002 + 0{,}01 \cdot 0{,}9998}\approx 0{,}0186$ .

Berechnung mittels Baumdiagramm

Ereignisbaum zum Beispiel

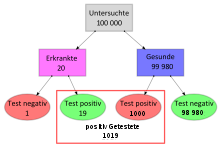
Probleme mit wenigen Klassen und einfachen Verteilungen lassen sich übersichtlich im Baumdiagramm für die Aufteilung der Häufigkeiten darstellen. Geht man von den Häufigkeiten auf relative Häufigkeiten bzw. auf (bedingte) Wahrscheinlichkeiten über, wird aus dem Baumdiagramm ein Ereignisbaum, ein Sonderfall des Entscheidungsbaums.

Den obigen Angaben folgend ergeben sich als absolute Häufigkeit bei 100 000 Personen 20 tatsächlich erkrankte Personen, 99 980 Personen sind gesund. Der Test diagnostiziert bei den 20 kranken Personen in 19 Fällen (95 Prozent Sensitivität) korrekt die Erkrankung. In einem Fall versagt der Test und zeigt die vorliegende Krankheit nicht an (falsch negativ). Bei wahrscheinlich 1000 der 99 980 gesunden Personen zeigt der Test fälschlicherweise eine Erkrankung an. Von den insgesamt 1019 positiv getesteten Personen sind also nur 19 tatsächlich krank ( $P(K\mid T) = \frac{19}{1019} \approx 0{,}0186$ ).

Bedeutung des Ergebnisses

Der Preis, 19 Träger der Krankheit zu finden, möglicherweise rechtzeitig genug für eine Behandlung oder Isolation, besteht nicht nur in den Kosten für 100 000 Tests, sondern auch in den unnötigen Ängsten und womöglich Behandlungen von 1000 falsch positiv Getesteten. Die Ausgangsfrage, ob bei diesen Zahlenwerten ein Massenscreening sinnvoll ist, ist daher wohl zu verneinen.

Die instinktive Annahme, dass eine – auf den ersten Blick eindrückliche – Sensitivität von 95 % bedeutet, dass eine positiv getestete Person auch tatsächlich mit hoher Wahrscheinlichkeit krank ist, ist also falsch. Dieses Problem tritt immer dann auf, wenn die tatsächliche Rate, mit der ein Merkmal in der untersuchten Gesamtmenge vorkommt, klein ist gegenüber der Rate der falsch positiven Ergebnisse.

Bayessche Statistik

→ Hauptartikel: Bayessche Statistik

Die Bayessche Statistik verwendet den Satz von Bayes im Rahmen der induktiven Statistik zur Schätzung von Parametern und zum Testen von Hypothesen.

Problemstellung

Folgende Situation sei gegeben: $\vartheta$ ist ein unbekannter Umweltzustand (z.B. ein Parameter einer Wahrscheinlichkeitsverteilung), der auf der Basis einer Beobachtung einer Zufallsvariable geschätzt werden soll. Weiterhin ist Vorwissen in Form einer A-priori-Wahrscheinlichkeitsverteilung des unbekannten Parameters $\vartheta$ gegeben. Diese A-priori-Verteilung enthält die gesamte Information über den Umweltzustand $\vartheta$ , die vor der Beobachtung der Stichprobe gegeben ist.

Je nach Kontext und philosophischer Schule wird die A-priori-Verteilung verstanden

als mathematische Modellierung des subjektiven degrees of belief (subjektiver Wahrscheinlichkeitsbegriff),
als adäquate Darstellung des allgemeinen Vorwissens (wobei Wahrscheinlichkeiten als natürliche Erweiterung der aristotelischen Logik in Bezug auf Unsicherheit verstanden werden – Cox' Postulate),
als aus Voruntersuchungen bekannte Wahrscheinlichkeitsverteilung eines tatsächlich zufälligen Parameters oder
als eine spezifisch gewählte Verteilung, die auf ideale Weise mit Unwissen über den Parameter korrespondiert (objektive A-priori-Verteilungen, zum Beispiel mithilfe der Maximum-Entropie-Methode).

Die bedingte Verteilung von unter der Bedingung, dass $\vartheta$ den Wert $\vartheta_0$ annimmt, wird im Folgenden mit $f(x \mid \vartheta_0 )$ bezeichnet. Diese Wahrscheinlichkeitsverteilung kann nach Beobachtung der Stichprobe bestimmt werden und wird auch als Likelihood des Parameterwerts $\vartheta_0$ bezeichnet.

Die A-posteriori-Wahrscheinlichkeit $P(\vartheta =\vartheta_0 \mid x)$ kann mit Hilfe des Satzes von Bayes berechnet werden. Im Spezialfall einer diskreten A-priori-Verteilung erhält man:

$P(\vartheta=\vartheta_0 \mid x) = \frac{f(x \mid \vartheta_0) \, P(\vartheta=\vartheta_0)}{\displaystyle\sum_{\vartheta' \in \Theta} f(x \mid \vartheta') \, P(\vartheta=\vartheta') }$

Falls die Menge aller möglichen Umweltzustände endlich ist, lässt sich die A-posteriori-Verteilung im Wert $\vartheta_0$ als die Wahrscheinlichkeit interpretieren, mit der man nach Beobachtung der Stichprobe und unter Einbeziehung des Vorwissens den Umweltzustand $\vartheta_0$ erwartet.

Als Schätzwert verwendet ein Anhänger der subjektivistischen Schule der Statistik in der Regel den Erwartungswert der A-posteriori-Verteilung, in manchen Fällen auch den Modalwert.

Beispiel

Ähnlich wie oben werde wieder eine Urne betrachtet, die mit zehn Kugeln gefüllt ist, aber nun sei unbekannt, wie viele davon rot sind. Die Anzahl $\vartheta$ der roten Kugeln ist hier der unbekannte Umweltzustand und als dessen A-priori-Verteilung soll angenommen werden, dass alle möglichen Werte von null bis zehn gleich wahrscheinlich sein sollen, d.h. es gilt $P(\vartheta=\vartheta_0) = \tfrac{1}{11}$ für alle $\vartheta_0 \in \{0,1,\dotsc,10\}$ .

Nun werde fünfmal mit Zurücklegen eine Kugel aus der Urne gezogen und bezeichne die Zufallsvariable, die angibt, wie viele davon rot sind. Unter der Annahme $\vartheta = \vartheta_0$ ist dann binomialverteilt mit den Parametern n = 5 und $p = \tfrac{\vartheta_0}{10}$ , es gilt also

$f(x \mid \vartheta_0) = \binom{5}{x} \left(\frac{\vartheta_0}{10}\right)^x \left(1-\frac{\vartheta_0}{10}\right)^{5-x}$

für $x \in \{0,1,\dotsc, 5\}$ .

Beispielsweise für x=2 , d.h. zwei der fünf gezogenen Kugeln waren rot, ergeben sich die folgenden Werte (auf drei Nachkommastellen gerundet)

$\vartheta_0$	0	1	2	3	4	5	6	7	8	9	10
$P(\vartheta = \vartheta_0)$	0,091	0,091	0,091	0,091	0,091	0,091	0,091	0,091	0,091	0,091	0,091
$P(\vartheta = \vartheta_0 \mid X = 2)$	0,000	0,044	0,123	0,185	0,207	0,188	0,138	0,079	0,031	0,005	0,000

Man sieht, dass im Gegensatz zur A-priori-Verteilung in der zweiten Zeile, in der alle Werte von $\vartheta$ als gleich wahrscheinlich angenommen wurden, unter der A-posteriori-Verteilung in der dritten Zeile $\vartheta = 4$ die größte Wahrscheinlichkeit besitzt, das heißt der A-posteriori-Modus ist .

Als Erwartungswert der A-posteriori-Verteilung ergibt sich hier:

$\sum _{\vartheta _{0}=0}^{10}\vartheta _{0}\cdot P(\vartheta =\vartheta _{0}\mid X=2)\approx 4{,}287$ .

Basierend auf einem Artikel in:

Wikipedia.de