Mächtigkeit (Mathematik)
In der Mathematik verwendet man den aus der Mengenlehre von Georg Cantor stammenden Begriff der Mächtigkeit oder Kardinalität, um den für endliche Mengen verwendeten Begriff der „Anzahl der Elemente einer Menge“ auf unendliche Mengen zu verallgemeinern.
Für endliche Mengen ist die Mächtigkeit gleich der Anzahl der Elemente der Menge, das ist eine natürliche Zahl einschließlich der Null. Für unendliche Mengen benötigt man etwas Vorarbeit, um ihre Mächtigkeiten zu charakterisieren. Die im Folgenden gemachten Definitionen und Folgerungen sind aber auch im Falle endlicher Mengen gültig.
Mächtigkeit bei endlichen Mengen
Bei einer endlichen Menge
bezeichnet die Mächtigkeit die Anzahl der Elemente von
.
Man notiert die Mächtigkeit von
durch
oder alternativ mit voranstehendem Doppelkreuz:
.
Beispiele:
Die Potenzmenge
einer endlichen Menge
hat genau
Elemente: Die Wahl einer Teilmenge entspricht den
unabhängigen Wahlen zwischen den zwei Möglichkeiten, ob ein bestimmtes Element
von
in der Teilmenge liegen soll oder nicht.
Gleichmächtigkeit, Mächtigkeit
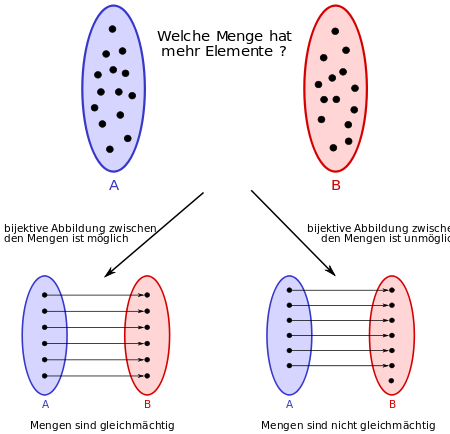
Man definiert zunächst den Begriff der Gleichmächtigkeit zweier beliebiger
Mengen
und
:
Eine Menge
heißt gleichmächtig (bei Cantor:
äquivalent) zu einer Menge
,
wenn es eine Bijektion
gibt. Man schreibt dann
oder
.
Die Gleichmächtigkeit
ist eine Äquivalenzrelation
auf der Klasse
aller Mengen, deren Äquivalenzklassen (bis auf die der Leermenge) echte Klassen
sind. Näheres siehe unten (Kardinalzahlen)
und Kardinalzahlen.
Ist
gleichmächtig zu
und
eine Bijektion zwischen
und
,
dann ist auch die Umkehrfunktion
von
eine Bijektion, also ist auch
gleichmächtig zu
.
Endliche Mengen sind genau dann gleichmächtig, wenn sie gleich viele Elemente
haben. Unendliche Mengen sind Mengen, die zu sich gleichmächtige echte
Teilmengen besitzen.
Man nennt eine Menge, die gleichmächtig zur unendlichen Menge
der natürlichen
Zahlen oder einer Teilmenge von ihr ist, die also mit natürlichen Zahlen
(einschließlich 0) „abgezählt“ werden kann, eine abzählbare
Menge.
Bisweilen versteht man auch abzählbar nur im Sinne von abzählbar
unendlich (= gleichmächtig zu )
und spricht dann an Stelle von abzählbar im Sinne der oben zuerst
eingeführten Definition von höchstens abzählbar, die die Formulierung
vieler Beweise etwas einfacher macht, und eher dem deutschen Sprachgebrauch
entspricht.
Besondere Ergebnisse:
- Gleichmächtig sind:
,
und
(also die Mengen der natürlichen, der ganzen und der rationalen Zahlen).
- Gleichmächtig sind:
,
,
und
, wobei
die Cantor-Menge ist.
- Die Menge
der reellen Zahlen ist mächtiger als
(also überabzählbar).
Kardinalzahlen
Da man leicht zeigen kann, dass die Gleichmächtigkeit von Mengen eine Äquivalenzrelation ist, ergibt die folgende Definition einen Sinn:
- Die Äquivalenzklassen der Mengen bezüglich der Relation der Gleichmächtigkeit nennt man Kardinalzahlen.
Aus technischen Gründen muss man aber ein geeignetes Repräsentantensystem finden: Indem man zeigt, dass jede Menge gleichmächtig zu einer wohlgeordneten Menge ist (dies ist die Aussage des Wohlordnungssatzes), kann man jede Kardinalzahl mit der kleinsten ihr gleichmächtigen Ordinalzahl gleichsetzen.
Aleph ()
ist der erste Buchstabe des hebräischen
Alphabets, er wird mit einem Index verwendet, um Kardinalzahlen unendlicher
Mengen zu benennen, siehe Aleph-Funktion.
Liegt eine Menge A in der Äquivalenzklasse (= Kardinalzahl) ,
dann sagt man, A hat die Mächtigkeit
.
Man schreibt dann:
.
Die Kardinalzahl einer endlichen Menge mit n Elementen wird mit der natürlichen Zahl n gleichgesetzt.
Man kann sich nun fragen, ob alle unendlichen Mengen einander gleichmächtig sind – in dem Fall wären alle unendlichen Mengen abzählbar. Es stellt sich jedoch heraus, dass es unendliche Mengen gibt, die nicht gleichmächtig zueinander sind, so ist etwa die Menge der natürlichen Zahlen nicht gleichmächtig zur Menge der reellen Zahlen. Das kann man zum Beispiel mit dem so genannten „Cantorschen Diagonalbeweis“ zeigen, siehe dazu den Artikel überabzählbar.
Weiter unten wird gezeigt, dass es unendlich viele verschiedene Kardinalzahlen gibt. Cantor selbst zeigte mit der ersten Cantorschen Antinomie, dass die Kardinalzahlen eine echte Klasse bilden.
Vergleich der Mächtigkeit
Um die Mächtigkeiten ungleichmächtiger Mengen vergleichen zu können, legt man
fest, wann eine Menge
mächtiger als eine Menge
sein soll:
- Wenn es eine Bijektion
von
auf eine Teilmenge von
gibt, dann heißt
höchstens gleichmächtig zu
. Man schreibt dann
.
- Wenn es eine Bijektion
von
auf eine Teilmenge von
gibt, aber keine Bijektion von
nach
existiert, dann heißt
weniger mächtig als
und
mächtiger als
. Man schreibt dann
. Offenbar gilt
genau dann, wenn
, aber nicht
ist.
Nun stellt sich aber die Frage nach der Vergleichbarkeit zweier beliebiger Mengen, ob also die bloße Eigenschaft, eine Menge zu sein, eine solche Vergleichsmöglichkeit impliziert. Und tatsächlich kann man für zwei beliebige Mengen im Allgemeinen zeigen (unter Verwendung des Auswahlaxioms):
- Sind
und
Mengen, dann gilt
oder
(Vergleichbarkeitssatz).
Des Weiteren kann man zeigen, dass jede abzählbare Menge entweder endlich
oder gleichmächtig zu
ist. Außerdem kann man zeigen, dass jede unendliche Menge eine zu
gleichmächtige Teilmenge enthält.
Damit ist die Mächtigkeit von
die kleinste unendliche Kardinalzahl. Man bezeichnet sie mit
:
.
Die Kontinuumhypothese
(CH) besagt, dass es keine Menge gibt, die mächtiger ist als ,
aber weniger mächtig als
. Wie der Name jedoch schon vermuten lässt, ist dies kein Satz in dem Sinne,
dass er sich beweisen lässt. Weder die Kontinuumhypothese noch ihre Verneinung
lässt sich aus den üblichen Axiomensystemen herleiten, zum Beispiel der
Zermelo-Fraenkel-Mengenlehre
mit Auswahlaxiom. Die Kontinuumhypothese besagt also, dass
die zweitkleinste unendliche Kardinalzahl
ist.
Totale Ordnung der Mächtigkeiten
Bei naiver Betrachtung der Schreibweise könnte man vermuten, dass für Mengen
und
mit
und
stets
gilt. Dass das tatsächlich so ist, wird vom folgenden Satz ausgesagt:
- Cantor-Bernstein-Schröder-Theorem:
Ist
höchstens gleichmächtig zu
und
höchstens gleichmächtig zu
, dann sind
und
gleichmächtig.
Fassen wir einige Eigenschaften der Mächtigkeiten zusammen:
- Es gilt stets
(man nehme die Identität als Bijektion).
- Aus
und
folgt
.
- Aus
und
folgt
(folgt sofort aus der Definition).
- Für zwei Mengen
und
gilt stets
oder
(das ist äquivalent zum Auswahlaxiom).
Damit ist gezeigt, dass die Kardinalzahlen total geordnet sind.
Rechenregeln bei endlichen Kardinalitäten
Es seien
sowie
endliche Mengen. Dann gelten folgende Regeln:
- Bijektions- oder Isomorphieregel
ist bijektiv auf
abbildbar
.
- Summenregel
Allgemein gilt.
Eine weitere Verallgemeinerung der Summenregel auf endlich viele endliche Menge ist das Prinzip von Inklusion und Exklusion. - Differenzenregel
- Produktregel
- Quotientenregel
Istund gilt
, so folgt
bzw.
- Subadditivität von Mengen
Falls diepaarweise disjunkt sind, so gilt die Gleichheit:
.
Das heißt also, dass bei disjunkten Mengen die Anzahl der Elemente in der Vereinigung der Mengengleich der Summe der einzelnen Anzahlen von Elementen in jeder dieser Mengen ist.
- Potenzregel
Bezeichnetdie Menge aller Abbildungen
, dann gilt
.
Beispiele
und
.
Dann
- existiert keine bijektive Abbildung zwischen
und
,
- ist
,
- lässt sich die Mächtigkeit der Differenz nicht mit obigem Satz bestimmen,
- beträgt die Mächtigkeit des kartesischen Produkts
.
In einem weiteren Beispiel sei
und
.
Dann
- existieren bijektive Abbildungen (identische Abbildung) zwischen den
beiden Mengen
und
,
- ist
, da die beiden Mengen identisch sind,
- ist
eine Teilmenge von
und somit gilt:
,
- die Mächtigkeit des kartesischen Produkts beträgt
und
- da
erhalten wir
bzw.
Mächtigkeit der Potenzmenge, größte Mächtigkeit
Die Frage nach der größten Mächtigkeit einer Menge beantwortet der Satz von Cantor:
- Für jede Menge
ist die Potenzmenge
mächtiger als
.
Für die Mächtigkeit von
gibt es auch folgende Schreibweise:
Zu beachten ist, dass der entsprechende Ausdruck für unendliche Ordinalzahlen
einen anderen Wert liefert, und z.B.
nicht als ein „Grenzwert“ einer Folge
angesehen werden kann.
Bestimmt man nun die Mächtigkeiten der Potenzmengen von Potenzmengen von Potenzmengen usw., dann sieht man, dass es unendlich viele Kardinalzahlen gibt, und keine mächtigste Menge existiert.
Literatur
- Erich Kamke: Mengenlehre (= Sammlung Göschen. Nr. 999). De Gruyter, Berlin 1928.
- Oliver Deiser: Einführung in die Mengenlehre: Die Mengenlehre Georg Cantors und ihre Axiomatisierung durch Ernst Zermelo. 3. Auflage. Springer, Berlin/Heidelberg 2010, ISBN 978-3-642-01444-4, doi:10.1007/978-3-642-01445-1.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 18.02. 2022