Prinzip von Inklusion und Exklusion

Das Prinzip von Inklusion und Exklusion (auch Prinzip der Einschließung und Ausschließung oder Einschluss-/Ausschluss-Verfahren) ist eine hilfreiche Technik zur Bestimmung der Mächtigkeit einer Menge. Sie findet vor allem in der Kombinatorik, der Zahlentheorie und der Stochastik Anwendung.

Das Prinzip drückt dazu die Kardinalität einer Ursprungsmenge durch die Kardinalitäten ihrer Teilmengen aus. Diese sind in aller Regel einfacher zu bestimmen. Namensgebend ist dabei das Vorgehen, bei welchem zunächst durch die Summe der Größe nicht notwendigerweise disjunkter Teilmengen die Größe von von oben abgeschätzt wird (Inklusion), anschließend jedoch durch die Subtraktion der Größe des gemeinsamen Schnittes der Teilmengen dies wieder zu korrigieren versucht wird (Exklusion).

Das Prinzip

Prinzip von Inklusion und Exklusion am Beispiel von drei Mengen

Es ist ein bekanntes Ergebnis, dass für je zwei endliche Mengen und

$|A\cup B|=|A|+|B|-|A\cap B|$

gilt. Hierbei kann man bereits das Prinzip von Inklusion und Exklusion erkennen. Durch |A|+|B| wird zunächst die Kardinalität von $|A\cup B|$ von oben abgeschätzt. Diese zu hohe Zahl wird anschließend durch die Subtraktion von $|A\cap B|$ korrigiert. Zweck dieser Korrektur ist es, diejenigen Elemente einmal wieder abzuziehen, die sowohl in als auch in enthalten sind und somit zunächst doppelt gezählt wurden.

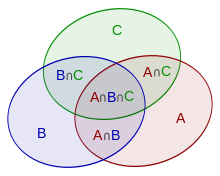
Anhand der nebenstehenden Abbildung lässt sich erkennen, dass eine Verallgemeinerung auf drei endliche Mengen

$|A\cup B\cup C|=|A|+|B|+|C|-|A\cap B|-|A\cap C|-|B\cap C|+|A\cap B\cap C|$

ergibt.

Im Allgemeinen wollen wir die Kardinalität der Vereinigung von endlichen Mengen

$X=A_{1}\cup A_{2}\cup \ldots \cup A_{n}$

bestimmen. Als erste Näherung erhalten wir durch Inklusion die Summe der Kardinalitäten der $A_{i}$ . Diese Summe ist in aller Regel jedoch zu groß, da wir Elemente aus dem Schnitt zweier Mengen $A_{i}\cap A_{j}$ mehrfach zählen würden, also

$|X|\leq \sum _{{1\leq i\leq n}}|A_{i}|~.$

Um dies zu korrigieren können wir nun durch Exklusion die Summe über die Kardinalität aller paarweisen Schnittmengen wieder abziehen. Dann gilt jedoch

$|X|\geq \sum _{{1\leq i\leq n}}|A_{i}|~-\sum _{{1\leq i<j\leq n}}|A_{i}\cap A_{j}|~,$

denn Elemente des Schnittes dreier Mengen $A_{i}\cap A_{j}\cap A_{k}$ würden – obwohl nur zweimal zu häufig bei der Inklusion mitgezählt – durch $|A_{i}\cap A_{j}|$ , durch $|A_{i}\cap A_{k}|$ und durch $|A_{j}\cap A_{k}|$ dreimal wieder abgezogen. Dies nun durch Inklusion, also durch Addition der Summe der Größe aller Schnitte aus drei Mengen, zu korrigieren führt zu

$|X|\leq \sum _{{1\leq i\leq n}}|A_{i}|~-\sum _{{1\leq i<j\leq n}}|A_{i}\cap A_{j}|~+\sum _{{1\leq i<j<k\leq n}}|A_{i}\cap A_{j}\cap A_{k}|~,$

darauf folgt durch Exklusion

$|X|\geq \sum _{{1\leq i\leq n}}|A_{i}|~-\sum _{{1\leq i<j\leq n}}|A_{i}\cap A_{j}|~+\sum _{{1\leq i<j<k\leq n}}|A_{i}\cap A_{j}\cap A_{k}|~-\sum _{{1\leq i<j<k<l\leq n}}|A_{i}\cap A_{j}\cap A_{k}\cap A_{l}|~,$

und so weiter, wobei beispielsweise $\sum _{{1\leq i<j<k\leq n}}$ bedeutet, dass über alle 3-Tupel (i,j,k) summiert wird, welche die Ungleichung $1\leq i<j<k\leq n$ erfüllen.

Satz

Es lässt sich folgende allgemeine Aussage beweisen. Gegeben sei eine endliche Menge , die sich als eine Vereinigung von Teilmengen $A_{1},A_{2},\ldots ,A_{n}$ schreiben lässt, d.h. $X=\bigcup _{{i=1}}^{n}A_{i}$ . Bezeichne im Folgenden zu einer Indexmenge $I\subseteq \{1,2,\ldots ,n\}$ die Menge $A_{I}$ den Schnitt über alle durch die Elemente der Indexmenge bezeichneten Teilmengen, also $A_{I}:=\bigcap _{{i\in I}}A_{i}$ , wobei $A_{\emptyset }=X$ entspricht. Dann gilt

$|X|=\sum _{{\emptyset \not =I\subseteq \{1,\ldots ,n\}}}\left(-1\right)^{{|I|+1}}|A_{I}|~.$

Mit anderen Worten: Betrachtet man alle möglichen Schnitte $A_{I}$ (außer dem leeren Schnitt $A_{\emptyset }$ ), so entspricht die Kardinalität von der Summe der Kardinalität aller Schnitte einer ungeraden Anzahl an Teilmengen (Inklusion) minus der Summe der Kardinalität aller Schnitte einer geraden Anzahl an Teilmengen (Exklusion), formal:

$|X|=\sum _{{{I\subseteq \{1,\ldots ,n\},} \atop {|I|~ungerade}}}|A_{I}|-\sum _{{{\emptyset \not =I\subseteq \{1,\ldots ,n\},} \atop {|I|~gerade}}}|A_{I}|$

Anwendung

Eine Anwendung des Prinzips liefert die Siebformel von Henri Poincaré und Sylvester bzw. der Additionssatz für Wahrscheinlichkeiten:

Für die Wahrscheinlichkeit von beliebigen Ereignissen $A_{i}$ aus einem Wahrscheinlichkeitsraum $(\Omega ,\Sigma ,P)$ gilt:

$P\left(\bigcup _{{i=1}}^{n}A_{i}\right)=\sum _{{k=1}}^{n}\left((-1)^{{k+1}}\!\!\sum _{{I\subseteq \{1,\dots ,n\}, \atop |I|=k}}\!\!\!\!P\left(\bigcap _{{i\in I}}A_{i}\right)\right)$ .

Aufgrund der Eigenschaft von Maßen, additiv zu sein, lässt sich der oben angegebene heuristische Beweis für das Prinzip von Inklusion und Exklusion, der mit Mitteln der elementaren Mengentheorie geführt wurde, direkt auf Wahrscheinlichkeiten übertragen.

Beispielsweise gilt für drei Ereignisse , und stets

$P(A\cup B\cup C)=P(A)+P(B)+P(C)-P(A\cap B)-P(A\cap C)-P(B\cap C)+P(A\cap B\cap C)$ .

Allgemein gilt diese Aussage auch schon für endliche Inhalte auf Ringen.

Basierend auf einem Artikel in:

Wikipedia.de