
Cantor-Menge
Unter der Cantor-Menge, auch cantorsches Diskontinuum, Cantor-Staub oder Wischmenge genannt, versteht man in der Mathematik eine bestimmte Teilmenge der Menge der reellen Zahlen mit besonderen topologischen, maßtheoretischen, geometrischen und mengentheoretischen Eigenschaften: Sie ist
- kompakt, perfekt, total unzusammenhängend (ein „Diskontinuum“) und nirgends dicht;
- eine Lebesgue-Nullmenge;
- selbstähnlich und hat eine nichtganzzahlige Hausdorffdimension (ist also ein Fraktal);
- gleichmächtig zum Kontinuum (der Menge aller reellen Zahlen), also insbesondere überabzählbar.
Die Cantormenge ist nach dem Mathematiker Georg Cantor benannt.
Für eine Definition und genauere Beschreibungen dieser Menge siehe unten.
Allgemeiner nennt man auch gewisse Mengen oder topologische Räume Cantormengen, wenn sie einen Teil dieser Eigenschaften besitzen. Welche dieser Eigenschaften gefordert werden, hängt dabei vom mathematischen Gebiet und oft auch vom Kontext ab. Ein topologischer Raum, der homöomorph zur Cantor-Menge ist, heißt Cantor-Raum.
Konstruktion
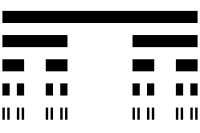
Schnitte von Intervallen
Die Cantor-Menge lässt sich mittels folgender Iteration konstruieren:
Man beginnt mit dem abgeschlossenen Intervall
der reellen
Zahlen von 0 bis 1. Aus diesem Intervall wird das offene mittlere Drittel
entfernt (weggewischt), also alle Zahlen, die strikt zwischen 1/3 und 2/3
liegen. Übrig bleiben die beiden Intervalle
und
.
Aus diesen beiden Intervallen wird wiederum jeweils das offene mittlere Drittel
entfernt und man erhält nun vier Intervalle:
,
,
und
.
Von diesen Intervallen werden wiederum die offenen mittleren Drittel entfernt.
Dieser Schritt wird unendlich oft wiederholt. Mathematisch lässt sich dies wie
folgt präzisieren: Ausgehend von der Menge
konstruiert man eine Funktion
,
welche das „Wegwischen“ formalisiert, und setzt dann
beziehungsweise als iterative Abbildungsvorschrift
oder in geschlossener Form
wobei
die n-fache Hintereinanderausführung
der Funktion
ist. Die Funktion lässt sich durch eine beliebige Menge
beschreiben als
,
wobei hier mit der Translation und Skalierung einer Menge die elementweise
Translation und Skalierung gemeint ist. Der Schnitt all dieser Mengen ist dann
die Cantormenge
Die Cantormenge besteht nun aus allen Punkten, die jedes Wegwischen überlebt
haben. Im Grenzfall (Schnitt über alle -ten
Wischmengen,
)
ist der Anteil am ursprünglichen Intervall Null, obwohl noch immer überabzählbar
viele Elemente vorliegen. Dieses Konstruktionsverfahren ist verwandt mit dem für
die Koch-Kurve.
Als triadische Entwicklung
Man kann die Cantormenge auch als die Menge aller Zahlen im Intervall
beschreiben, die eine Darstellung als Kommazahl
zur Basis 3 besitzen, in der nur die Ziffern 0 und 2 vorkommen. Die Darstellung
zur Basis Drei wird auch triadische Entwicklung genannt. Jede Zahl aus dem
Intervall
lässt sich darstellen als
,
wobei
ist. So ist zum Beispiel
.
Somit ist
und
wenn
.
Es lässt sich zeigen, dass die oben konstruierte Menge
dann genau der Menge der Zahlen entspricht, bei denen bis zu der n-ten Stelle
ihrer triadischen Entwicklung nur eine Null oder eine Zwei steht.
Der Schnitt all dieser Mengen ist wieder die Cantor-Menge und enthält damit
alle Zahlen, deren triadsche Entwicklung keine eins enthält. Insbesondere
enthält die Cantormenge mehr als nur die Randpunkte der entfernten Intervalle;
diese Randpunkte sind genau die Zahlen in ,
welche sich mit einer 0-Periode oder mit einer 2-Periode schreiben lassen, zum
Beispiel
ist der linke Randpunkt des im ersten Schritt entfernten Intervalls. Die Verwendung der Ziffer 1 wird durch die 2-Periode umgangen, welche dieselbe Zahl darstellt. (Dies ist nur für eine 1 direkt vor der 0-Periode möglich. An anderer Stelle kann aber keine 1 auftreten, da die Zahl sonst mitten in einem der gestrichenen Intervalle läge.) Darüber hinaus ist aber z.B. auch 1/4 in der Cantormenge, denn
Eigenschaften
- Die Hausdorff-Dimension
und die Minkowski-Dimension
der Cantormenge betragen
. Dies folgt aus der Tatsache, dass in jedem Konstruktionsschritt zwei Kopien der Menge erzeugt werden, die um den Faktor
skaliert werden.
- Das eindimensionale Lebesgue-Borel-Maß
der Cantor-Menge ist Null, sie ist also eine
-Nullmenge. Zunächst ist
abgeschlossen, also in der Borelschen σ-Algebra enthalten und demnach Borel-messbar. Der Cantor-Menge lässt sich also sinnvoll ein Maß zuordnen. Bei der Iteration der Funktion
verdoppelt sich nun durch die Translation in jedem Schritt die Anzahl der Intervalle, wobei sich die Länge jedes Intervalles in jedem Schritt drittelt. Da alle Intervalle disjunkt sind, gilt dann Aufgrund der σ-Additivität des Lebesgue-Borel-Maßes
.
- Somit ist auch das Lebesgue-Maß der Cantor-Menge gleich Null, da die Borelsche σ-Algebra in der Lebesgueschen σ-Algebra enthalten ist und die Maße dort übereinstimmen.
- Die Cantor-Menge ist abgeschlossen
in
: in jedem Iterationsschritt werden offene Mengen entfernt, die Vereinigung dieser Mengen ist dann offen und das Komplement der Cantor-Menge. Somit ist die Cantormenge abgeschlossen.
- Mit der Beschränktheit der Cantor-Menge und dem Satz von Heine-Borel folgt daraus, dass die Cantor-Menge kompakt ist.
- Die Überabzählbarkeit
der Cantor-Menge lässt sich mit einem Diagonalisierbarkeitsargument
und der triadischen Entwicklung der Zahlen in der Cantor-Menge zeigen. Die
Zahlen in der Cantor-Menge sind dargestellt in ihrer triadischen Entwicklung
alle Elemente von
, also Folgen, die nur die Null und die Zwei enthalten. Nimmt man die Abzählbarkeit dieser Menge an, kann man dies zum Widerspruch führen, indem man eine Zahl mit einer triadischen Entwicklung konstruiert, die nicht in der Abzählung enthalten ist.
0-1-Folgen
Das kartesische
Produkt abzählbar unendlich vieler Kopien der zweielementigen Menge
ist die Menge aller unendlichen Folgen, die nur die Werte 0 und 1 annehmen, d.h.
die Menge aller Funktionen
.
Diese Menge wird mit
bezeichnet. Durch die oben genannte triadische Entwicklung lässt sich eine
natürliche Bijektion zwischen der Cantormenge und der Menge
angeben: Die Zahl mit der triadischen Entwicklung
wird in die Folge
übersetzt; die Zahl 1/4 entspricht also der Folge
.
Die Menge
trägt auch eine natürliche Topologie (nämlich die Produkttopologie, die
durch die diskrete
Topologie auf der Menge
induziert wird). Die gerade genannte Abbildung ist ein Homöomorphismus
zwischen der Cantormenge und dem topologischen Raum
.
Dieser wird daher als Cantor-Raum
bezeichnet.
Cantor-Verteilung und Cantorfunktion
Eng verwandt mit der Cantormenge ist die Cantor-Verteilung. Sie wird ähnlich wie die Cantormenge konstruiert. Ihre Verteilungsfunktion wird auch Cantorfunktion bezeichnet.
Die Cantorverteilung dient häufig als Beispiel für die Existenz von stetigsingulären Verteilungen, welche singulär bezüglich des Lebesgue-Maßes sind, aber dennoch eine stetige Verteilungsfunktion besitzen (Funktionen mit sog. singulär-kontinuierlichem Verhalten).
Andere Cantormengen
Die Cantormenge (auch Mitteldrittel-Cantormenge, middle thirds Cantor set) wurde oben beschrieben. Unter einer Cantormenge versteht man eine Menge von reellen Zahlen, die man mit einer Variante des obigen Wischprozesses bekommt, wobei man nun die Längen und Anzahlen der weggewischten Intervalle variieren kann:
Man beginnt mit einem beliebigen Intervall
von reellen Zahlen. Im ersten Schritt entfernt man endlich viele offene
disjunkte Unterintervalle (mindestens aber eines) und erhält so endlich viele
abgeschlossene Intervalle (mindestens 2).
Im zweiten Schritt entfernt man aus jedem der enthaltenen Intervalle wiederum endlich viele Unterintervalle (jeweils mindestens eines).
Wiederum definiert dieser Prozess eine Menge von reellen Zahlen, nämlich jene Punkte, die niemals in eines der weggewischten Intervalle gefallen sind.
Man kann zeigen, dass alle so konstruierten Cantormengen zueinander homöomorph sind und dass sie insbesondere zur Menge aller reellen Zahlen gleichmächtig sind. Indem man die Proportion „Längen der weggewischten Intervalle: Längen der übrigbleibenden Intervalle“ geeignet variiert, kann man eine Cantormenge erzeugen, deren Hausdorff-Dimension eine beliebige vorgegebene Zahl im Intervall [0,1] ist.
Ein zweidimensionales Analogon der Cantor-Menge ist der Sierpinski-Teppich, ein dreidimensionales der Menger-Schwamm.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 10.01. 2021