Topologischer Raum

Beispiele und Gegenbeispiele zu Topologien – die sechs Abbildungen stellen Teilmengen der Potenzmenge von {1,2,3} dar (der kleine Kreis links oben ist jeweils die leere Menge). Die ersten vier sind Topologien; im Beispiel unten links fehlt {2,3}, unten rechts {2} zur Topologie-Eigenschaft.

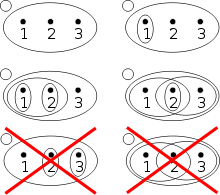
Ein topologischer Raum ist der grundlegende Gegenstand der Teildisziplin Topologie der Mathematik. Durch die Einführung einer topologischen Struktur auf einer Menge lassen sich intuitive Lagebeziehungen wie „Nähe“ und „Streben gegen“ aus dem Anschauungsraum auf sehr viele und sehr allgemeine Strukturen übertragen und mit präziser Bedeutung versehen.

Definition

Eine Topologie ist ein Mengensystem bestehend aus Teilmengen einer Grundmenge , die offen oder offene Mengen genannt werden, und die die folgenden Axiome erfüllen:

• Die leere Menge und die Grundmenge sind offen.
• Der Durchschnitt endlich vieler offener Mengen ist offen. (Es genügt zu fordern, dass der Durchschnitt von zwei offenen Mengen offen ist.)
• Die Vereinigung beliebig vieler offener Mengen ist offen.

Man nennt dann eine Topologie auf , und das Paar einen topologischen Raum.

Grundbegriffe

Sprechweise: Elemente sind Punkte, die Menge ist ein Raum

Aus dem Anschauungsraum hat sich die Bezeichnung „Punkt“ für die Elemente der Grundmenge und die Bezeichnung „(topologischer) Raum“ für die Menge , die die topologische Struktur trägt, durchgesetzt. Formal korrekt ist ein topologischer Raum aber das Paar aus der strukturtragenden Menge und dem strukturdefinierenden System (der „Topologie“) von Teilmengen.

Dual: abgeschlossen

Eine Teilmenge des topologischen Raums , deren Komplement eine offene Menge ist, heißt abgeschlossen. Wenn man die oben formulierte Definition dualisiert und das Wort „offen“ durch „abgeschlossen“ ersetzt (sowie Schnitt und Vereinigung vertauscht), ergibt sich eine gleichwertige Definition des Begriffs „topologischer Raum“ über dessen System abgeschlossener Mengen.

Umgebungen

In einem topologischen Raum hat jeder Punkt einen Filter von Umgebungen. Damit lässt sich der intuitive Begriff von „Nähe“ mathematisch fassen. Auch dieser Begriff kann einer Definition des Topologischen Raums zugrunde gelegt werden.

Vergleich von Topologien: gröber und feiner

Auf einer festen Menge kann man gewisse Topologien und miteinander vergleichen: Man nennt eine Topologie feiner als eine Topologie , wenn ist, wenn also jede in offene Menge auch in offen ist. heißt dann gröber als . Sind die beiden Topologien verschieden, sagt man auch, sei echt feiner als , und sei echt gröber als .

Es gibt im Allgemeinen auf auch Topologien und , die sich nicht in diesem Sinn vergleichen lassen. Für sie existiert eine eindeutige gemeinsame Verfeinerung, das ist die gröbste Topologie auf , die beide Topologien umfasst. Dual zu dieser gemeinsamen Verfeinerung ist die durch die Schnittmenge gegebene Topologie. Sie ist die feinste Topologie, die in beiden Topologien enthalten ist. Durch die Relation „ist feiner als“ werden die Topologien auf einer Menge zu einem Verband.

Diese Sprechweise ist kompatibel mit der „feiner“-Ordnung der Umgebungssysteme als Filter: Ist ein fester Punkt des Raums, dann ist der von der feineren Topologie erzeugte Umgebungsfilter feiner als der von der gröberen Topologie erzeugte .

Morphismen: Stetige Abbildungen

Wie bei jeder mathematischen Struktur gibt es auch bei den topologischen Räumen strukturerhaltende Abbildungen (Morphismen). Hier sind es die stetigen Abbildungen: Eine Abbildung ist (global) stetig, wenn das Urbild jeder offenen Teilmenge von eine offene Menge in ist, formal: .

Die Isomorphismen heißen hier Homöomorphismen, dies sind bijektive stetige Abbildungen, deren Umkehrung ebenfalls stetig ist. Strukturell gleichartige (isomorphe) topologische Räume nennt man homöomorph.

Beispiele

Topologische Räume in Bezug zu anderen Nähe definierenden Strukturen

• Auf jeder Grundmenge existieren als triviale Beispiele von Topologien:
  1. Die indiskrete Topologie, die nur die leere Menge und die Grundmenge enthält. Sie ist die gröbste Topologie auf .
  2. Die diskrete Topologie, die alle Teilmengen enthält. Sie ist die feinste Topologie auf .
• Auf einer unendlichen Menge (z.B. der Menge der natürlichen Zahlen) kann man die kofinite Topologie einführen: Offen ist die leere Menge sowie jede Teilmenge von , deren Komplement nur endlich viele Elemente enthält.
• Jede streng totalgeordnete Menge kann man in natürlicher Weise mit ihrer Ordnungstopologie versehen.
• Die offenen Kugeln in einem metrischen Raum erzeugen (als Basis) eine Topologie, die von der Metrik induzierte Topologie.
  • Spezielle metrische Räume sind die normierten Räume, hier wird die Metrik und damit die natürliche Topologie (Normtopologie) von der Norm induziert.
• Einige konkrete topologische Räume mit speziell konstruierten Eigenschaften tragen die Namen ihrer Entdecker, z.B. Arens-Fort-Raum, Cantor-Raum, Hilbertwürfel, Michael-Gerade, Niemytzki-Raum, Sorgenfrey-Ebene, Tichonow-Planke etc.

Erzeugung topologischer Räume

• Man kann ein beliebiges System von Teilmengen einer Menge zu einer Topologie auf erweitern, indem man fordert, dass (mindestens) alle Mengen aus offen sind. Damit wird zur Subbasis einer Topologie auf .
• Jeder Teilmenge eines topologischen Raums kann eine Unterraumtopologie zugeordnet werden. Dabei sind die offenen Mengen gerade die Schnitte der in offenen Mengen mit der Teilmenge .
• Bei jeder Familie von topologischen Räumen kann das mengentheoretische Produkt der Grundmengen mit der Produkttopologie versehen werden:
  • Bei endlichen Produkten bilden die Produkte der offenen Mengen aus den Faktorräumen eine Basis dieser Topologie.
  • Bei unendlichen Produkten bilden diejenigen Produkte von offenen Mengen aus den Faktorräumen eine Basis, bei denen alle bis auf endlich viele Faktoren jeweils den ganzen betreffenden Raum umfassen.
  • Wählt man in einem unendlichen Produkt als Basis die kartesischen Produkte von offenen Mengen aus den Faktorräumen, dann erhält man die Box-Topologie auf dem Produkt. Diese ist (i.A. echt) feiner als die Produkttopologie.
• Eine Verallgemeinerung der Beispiele Unterraum- und Produkttopologie ist die Konstruktion einer Initialtopologie. Hier wird die Topologie auf einer Menge durch die Forderung definiert, dass bestimmte Abbildungen aus in andere topologische Räume stetig sein sollen. Die Initialtopologie ist die gröbste Topologie auf mit dieser Eigenschaft.
• Eine Quotiententopologie entsteht, indem man in einem topologischen Raum gewisse Punkte miteinander verklebt (identifiziert). Formal geschieht dies durch eine Äquivalenzrelation, die Punkte des Quotientenraums sind also Klassen von Punkten aus .
• Eine Verallgemeinerung des Beispiels Quotiententopologie ist die Konstruktion einer Finaltopologie. Hier wird die Topologie auf einer Menge durch die Forderung definiert, dass bestimmte Abbildungen aus anderen topologischen Räumen nach stetig sein sollen. Die Finaltopologie ist die feinste Topologie auf mit dieser Eigenschaft.

Basierend auf einem Artikel in: Wikipedia.de
 

Seite zurück
©  biancahoegel.de;
Datum der letzten Änderung: Jena, den: 28.11. 2023