
Quotiententopologie
Die Quotiententopologie (auch Identifizierungstopologie genannt) ist ein Begriff aus dem mathematischen Teilgebiet der Topologie. Anschaulich entsteht diese Topologie, wenn man Punkte „zusammenklebt“, d.h. zwei ehemals verschiedene Punkte als ein und denselben Punkt identifiziert. Solche Punkte werden mittels Äquivalenzrelationen festgelegt. Das geschieht im Allgemeinen, um neue topologische Räume aus bestehenden abzuleiten. Zu einer Verallgemeinerung dieser Konstruktion vergleiche den Artikel Finaltopologie.
Definition
Es sei
ein topologischer
Raum und
eine surjektive
Abbildung von Mengen.
Dann ist die durch
induzierte Quotiententopologie auf
diejenige, in der eine Teilmenge
genau dann offen ist, wenn das Urbild
offen ist.
Eigenschaften
- Die Quotiententopologie ist die feinste
Topologie auf
, für die die Abbildung
stetig ist.
- Versieht man
mit der Quotiententopologie, so ist
eine Quotientenabbildung: Ist
ein weiterer topologischer Raum und
eine Abbildung der zugrundeliegenden Mengen, so ist
genau dann stetig, wenn
stetig ist (universelle Eigenschaft der Quotiententopologie):
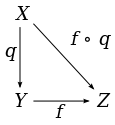
Wichtige Spezialfälle
- Ist
eine Äquivalenzrelation auf einem topologischen Raum, so versieht man die Menge
der Äquivalenzklassen meist ohne weitere Erwähnung mit der von der kanonischen Abbildung
induzierten Quotiententopologie.
- Ist insbesondere
eine topologische Gruppe und
eine Untergruppe von
, so versieht man die homogenen Räume
und
mit der Quotiententopologie.
- Zusammenschlagen eines Teilraumes zu einem Punkt: Ist
ein topologischer Raum und
eine Teilmenge von
, so bezeichnet
die Menge der Äquivalenzklassen bezüglich der Äquivalenzrelation, bei der zwei Punkte
äquivalent heißen, wenn sie gleich sind oder beide in
liegen. Die Abbildung
ist außerhalb von
injektiv, und das Bild von
ist ein einzelner Punkt.
Beispiele
- Es sei
das Einheitsintervall und
die Einheitskreislinie. Dann ist die durch die Abbildung
-
- induzierte Quotiententopologie auf
gleich der Teilraumtopologie von
als Teilmenge von
.
- Ist
das Einheitsintervall und
, so ist der durch Zusammenschlagen von
zu einem Punkt entstehende Raum
homöomorph zur Kreislinie
. Dies ist im Wesentlichen dasselbe wie das erste Beispiel, jedoch waren dort die Zielmenge und die Abbildung schon explizit gegeben, hier entstand sie erst durch die beim Zusammenschlagen implizite Äquivalenzrelation.
- Der homogene Raum
ist ebenfalls homöomorph zur Kreislinie
- Im Gegensatz dazu besteht der Raum, den man erhält, wenn man die Teilmenge
von
zu einem Punkt zusammenschlägt, anschaulich gesprochen aus abzählbar unendlich vielen Kreisen, die in einem Punkt zusammengeklebt wurden.
- Ist
eine ganze Ringerweiterung, so ist die durch die induzierte stetige Spektrenabbildung
induzierte Quotiententopologie auf
identisch mit der Zariski-Topologie auf diesem Raum.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 10.09. 2019