Verband (Mathematik)

Ein Verband ist in der Mathematik eine Struktur, die sowohl als Ordnungsstruktur als auch als algebraische Struktur vollständig beschrieben werden kann. Als Ordnungsstruktur ist ein Verband dadurch gekennzeichnet, dass es zu je zwei Elementen , ein Supremum $a\vee b$ gibt, d.h. ein eindeutig bestimmtes kleinstes Element, das größer oder gleich und ist, und umgekehrt ein Infimum $a\wedge b$ , ein größtes Element, das kleiner oder gleich und ist. Als algebraische Struktur ist ein Verband dadurch gekennzeichnet, dass es zwei assoziative und kommutative Operationen gibt, für die die Absorptionsgesetze kennzeichnend sind: Für beliebige Elemente gilt

$u\vee (u\wedge v)=u$ und $u\wedge (u\vee v)=u$ .

Für jede in der Verbandstheorie vorkommende algebraische Aussage gibt es eine direkte Übersetzung in eine Ordnungsaussage und umgekehrt. Diese Übersetzung ist in den meisten Fällen auch anschaulich nachzuvollziehen. Die Möglichkeit, Ergebnisse doppelt zu interpretieren und dadurch besser zu verstehen, macht die Untersuchung und die Verwendung von Aussagen aus der Verbandstheorie so interessant. Der Begriff Verband wurde im hier beschriebenen Sinne von Fritz Klein-Barmen geprägt.

Obwohl diese doppelte Charakterisierung auf den ersten Blick sehr speziell aussieht, treten Verbände häufig auf:

die z.B. in der Mengenlehre, der Logik und als Schaltalgebren auftretenden Booleschen Algebren sind Verbände.
totale Ordnungen, die z.B. in den verschiedenen Zahlbereichen wie $\mathbb {N}$ (natürliche Zahlen), $\mathbb {Z}$ (ganze Zahlen), $\mathbb {Q}$ (rationale Zahlen) oder $\mathbb {R}$ (reelle Zahlen) auftreten, sind Verbände.
für jede beliebige natürliche Zahl ist die Menge der Teiler (durch die Teilbarkeit geordnet) ein Verband.
die Unterstrukturen einer beliebigen algebraischen oder sonstigen Struktur bilden einen Verband mit der Teilmengenrelation als Ordnung.

In der Literatur sind auch die Symbole $\sqcup$ und $\sqcap$ verbreitet. Diese Notation wird hier aufgrund von technischen Einschränkungen nicht verwendet.

Präzisierung

Verbände als algebraische Strukturen

Ein Verband $(V,\vee ,\wedge )$ ist eine Menge mit zwei inneren binären Verknüpfungen $\vee$ (Vereinigung, engl. join) und $\wedge$ (Durchschnitt, engl. meet), die folgenden Bedingungen für alle , , aus genügen:

Assoziativgesetze:

$u\vee (v\vee w)=(u\vee v)\vee w$ ,
$u\wedge (v\wedge w)=(u\wedge v)\wedge w$ .

Kommutativgesetze:

$u\vee v=v\vee u$ ,
$u\wedge v=v\wedge u$ .

Absorptionsgesetze:

$u\vee (u\wedge v)=u$ ,
$u\wedge (u\vee v)=u$ .

Aus diesen Bedingungen folgt die Idempotenz beider Verknüpfungen:

$u\vee u=u$ ,
$u\wedge u=u$ .

ist also bezüglich jeder einzelnen Verknüpfung ein Halbverband, d.h. eine kommutative Halbgruppe, in der jedes Element idempotent ist. Die Verknüpfungen treten bei den Absorptionsgesetzen in Wechselwirkung.

Verbände als Ordnungsstrukturen

Man kann nach einer Idee von Leibniz auf eine Halbordnung definieren durch:

$v\leq w\quad \iff \quad v\wedge w=v.$

Mit dem Absorptionsgesetz erkennt man die Gültigkeit der Äquivalenzen

$v\leq w\quad \iff \quad v\wedge w=v\quad \iff \quad v\vee w=w.$

Bezüglich dieser Halbordnung hat jede zweielementige Teilmenge $\{v,w\}$ ein Supremum (obere Grenze) $s=v\vee w$ und ein Infimum (untere Grenze) $i=v\wedge w$ . Dabei ist ein Element ein Supremum von $\{v,w\}$ , wenn gilt:

$v\leq s$ und $w\leq s$ (d.h. ist obere Schranke).
Aus $v\leq t$ und $w\leq t$ folgt $s\leq t$ (d.h. ist die kleinste obere Schranke).

Analoges gilt für das Infimum . Man kann per Induktion zeigen, dass jede nichtleere endliche Teilmenge ein Supremum und ein Infimum hat. Man schreibt allgemein das Supremum einer Menge als $\bigvee M$ , und das Infimum von als $\bigwedge M$ , falls diese existieren.

Umgekehrt kann man für eine halbgeordnete Menge, bei der jede zweielementige Teilmenge ein Infimum und ein Supremum hat, definieren:

$v\wedge w=\inf\{v,w\}$ und $v\vee w=\sup\{v,w\}$ .

Die beiden Verknüpfungen erfüllen dann die Verbandsaxiome, wie man leicht nachrechnet.

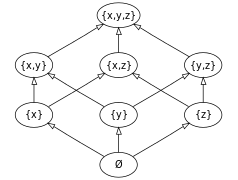
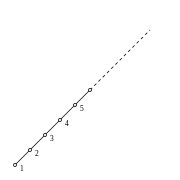
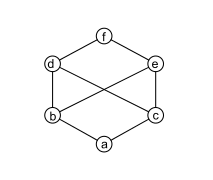
Hasse-Diagramme für einige Beispiele

→ Hauptartikel: Hasse-Diagramm

Eine endliche halbgeordnete Menge $(M,{\leq })$ kann man durch einen gerichteten Graphen darstellen, den man Hasse-Diagramm nennt.

Wenn man den Graph so anordnet, dass alle Kanten von unten nach oben gerichtet sind, dann kann man die Ordnung leicht sehen:

ist dann gleichwertig mit: ist durch einen (nach oben führenden) Kantenzug mit verbunden.

Hasse-Diagramme für einige Verbände

Verband der Teilmengen von {x,y,z} (eine Boolesche Algebra)

Verband der Teiler von 60

Lattice of partitions of an order 4 set.svg

Partitionen der Menge {1,2,3,4}, durch gröber = geordnet

Verband, der nicht distributiv, aber orthokomplementierbar ist

Die Menge der natürlichen Zahlen: Total geordnete Mengen sind Verbände

Diagramme, die keine Verbände darstellen

kein Verband, da c⊔d nicht existiert

kein Verband, da b⊔c nicht existiert (d und e sind zwar beide minimal größer, aber keins von beiden ist kleinstes der größeren Elemente)

Spezielle Elemente in Verbänden

Neutrale Elemente

Falls die Verknüpfung $\vee$ ein neutrales Element $0$ hat,

$0\vee a=a,$

dann ist es eindeutig bestimmt und man nennt es das Nullelement des Verbandes. Bzgl. $\wedge$ ist $0$ absorbierend und bzgl. der Ordnung das kleinste Element:

$0\wedge a=0$ und

$\bigwedge V.$

Man nennt den Verband dann nach unten beschränkt.

Falls die Verknüpfung $\wedge$ ein neutrales Element hat,

$1\wedge a=a,$

dann ist es eindeutig bestimmt und man nennt es das Einselement des Verbandes. Bzgl. $\vee$ ist absorbierend und bzgl. der Ordnung das größte Element:

$1\vee a=1$ und

$\bigvee V.$

Man nennt den Verband dann nach oben beschränkt.

Ein Verband heißt beschränkt, wenn er nach unten und nach oben beschränkt ist, also für beide Verknüpfungen ein neutrales Element hat.

Komplementäre Elemente

Für ein gegebenes Element eines beschränkten Verbandes nennt man ein Element mit der Eigenschaft

$a\wedge b=0$ und $a\vee b=1$

ein Komplement von .

Ein beschränkter Verband, in dem jedes Element (mindestens) ein Komplement hat, heißt komplementärer Verband.

Im Allgemeinen kann es zu einem Elemente mehrere komplementäre Elemente geben.

Es gilt aber: In einem distributiven beschränkten Verband ist das Komplement eines Elements im Falle seiner Existenz eindeutig bestimmt. Man schreibt es oft als $a^{c}$ (vor allem bei Teilmengenverbänden), $\neg a$ (vor allem bei Anwendungen in der Logik) oder ${\bar {a}}$ .

In jedem beschränkten Verband gilt

$\neg 0=1,\neg 1=0$ .

In einem distributiven beschränkten Verband gilt: Falls ein Komplement $\neg a$ hat, dann hat auch $\neg a$ ein Komplement, nämlich:

$\neg (\neg a)=a$ .

Spezielle Verbände

Modulare Verbände

$N_{5}$ , der minimale nicht-modulare Verband

Ein Verband heißt modular, falls gilt:

$u\leq w\Longrightarrow u\vee (v\wedge w)=(u\vee v)\wedge w$ für alle $u,v,w\in V$ .

Für einen Verband sind wiederum jeweils äquivalent:

ist modular.
$u\geq w\Longrightarrow u\wedge (v\vee w)=(u\wedge v)\vee w$ für alle $u,v,w\in V$ .
$u\vee (v\wedge (u\vee w))=(u\vee v)\wedge (u\vee w)$ für alle $u,v,w\in V$ .
$u\wedge (v\vee (u\wedge w))=(u\wedge v)\vee (u\wedge w)$ für alle $u,v,w\in V$ .

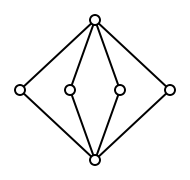
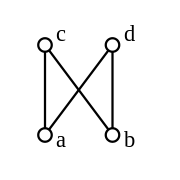
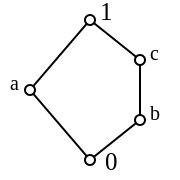
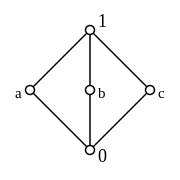
Ein nicht modularer Verband enthält immer den Verband $N_{5}$ als Unterverband.

Distributive Verbände

$M_{3}$ , der minimale modulare, nicht-distributive Verband

Im Folgenden meinen wir mit dem Verband stets den Verband $(V,\vee ,\wedge )$ .

Ein Verband heißt distributiv, wenn die Verknüpfungen in doppelter Hinsicht distributiv sind:

$u\vee (v\wedge w)=(u\vee v)\wedge (u\vee w)$ für alle $u,v,w\in V$ und
$u\wedge (v\vee w)=(u\wedge v)\vee (u\wedge w)$ für alle $u,v,w\in V$ .

Da diese beiden Aussagen zueinander äquivalent sind, genügt es, die Gültigkeit eines dieser beiden Distributivgesetze zu verlangen.

Jeder distributive Verband ist modular, aber nicht umgekehrt. Ein modularer Verband, der nicht distributiv ist, enthält immer den Verband $M_{3}$ , den Verband der Untergruppen der Kleinschen Vierergruppe als Unterverband.

Dies ergibt den Test: hat ein Verband weder einen Unterverband der Form $N_{5}$ noch einen der Form $M_{3}$ , dann ist er distributiv.

Distributive Verbände sind auch anders zu charakterisieren, denn Garrett Birkhoff (1933) und Marshall Harvey Stone (1936) haben gezeigt:

Ein Verband ist genau dann distributiv, wenn er isomorph zu einem Mengenverband ist.

Boolesche Algebren

→ Hauptartikel: Boolesche Algebra

Ein distributiver komplementärer Verband heißt Boolesche Algebra oder Boolescher Verband;

Eine weitere Verallgemeinerung, bei der statt Komplementen nur relative Pseudokomplemente gefordert werden, heißt Heyting-Algebra.

Vollständige Verbände

Ein Verband heißt vollständig, wenn jede (auch die leere ebenso wie gegebenenfalls unendliche) Teilmenge ein Supremum und ein Infimum hat.

Es genügt, für jede Teilmenge die Existenz des Supremums zu verlangen, denn es ist

$\bigwedge M=$ $\bigvee \{x\in V:(\forall \,y\in M:x\leq y)\}.$

Jeder vollständige Verband ist beschränkt mit

$0=\bigwedge V=\bigvee \emptyset$ und $1=\bigvee V=\bigwedge \emptyset .$

Jeder endliche, nichtleere Verband ist vollständig, also auch beschränkt.

Längenendliche Verbände

Wenn jede bezüglich der Ordnung totalgeordnete Teilmenge (Kette) endlich ist, nennt man den Verband längenendlich. Für viele Beweise innerhalb der Verbandstheorie muss ein Verband nicht endlich sein, sondern es reicht, wenn er längenendlich ist.

Kompakte Elemente und algebraische Verbände

Man nennt ein Element eines vollständigen Verbandes kompakt (nach der verwandten Eigenschaft kompakter Räume in der Topologie), wenn jede Teilmenge von mit

$a\leq \bigvee M$

eine endliche Teilmenge enthält, für die gilt:

$a\leq \bigvee E$

Ein Verband heißt algebraisch, wenn er vollständig ist und wenn jedes Element von das Supremum von kompakten Elementen ist.

Dualität in Verbänden

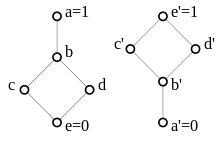
Die beiden Verbände sind dual zueinander (aber offensichtlich nicht isomorph).

Vertauscht man in einem Verband die beiden Verknüpfungen $\wedge$ und $\vee$ , erhält man eine neue Struktur . Man nennt die duale Struktur.

Ersetzt man in einer beliebigen Formel $\varphi$ der Sprache der Verbandstheorie und setzt überall die beiden Zeichen $\wedge$ und $\vee$ wechselseitig füreinander ein und ersetzt außerdem überall 0 durch 1 und umgekehrt, dann nennt man die entstandene Formel ${\widehat {\varphi }}$ die duale Formel von $\varphi$ .

Offensichtlich gelten in dem zu dualen Verband die dualen zu den in gültigen Formeln. Da in der Definition eines Verbands zu jeder Formel auch die duale Formel vorkommt, folgt, dass ebenfalls ein Verband ist, der als der zu duale Verband bezeichnet wird.

Aus dieser Beobachtung folgt:

Gilt eine Formel in allen Verbänden, dann gilt auch ihre duale Formel in allen Verbänden.

Das Modularitätsgesetz ist selbstdual und die beiden Distributiv-Gesetze sind zueinander dual und die beiden Komplementärgesetze sind zueinander dual. Daher gilt entsprechend:

Gilt eine Formel in allen modularen oder in allen distributiven Verbänden oder in allen Booleschen Algebren, dann gilt auch die duale Formel in den entsprechenden Verbänden.

Unterstrukturen

Unterverbände

Ein Unterverband von ist eine Teilmenge , die mit den eingeschränkten Verknüpfungen von ein Verband ist, d.h. es liegen

$a\vee b$ und $a\wedge b$ in für alle aus

Teilverbände

Ein Teilverband von ist eine Teilmenge , die ein Verband ist, d.h. ist eine halbgeordnete Menge mit Supremum und Infimum für endliche Teilmengen.

Natürlich ist jeder Unterverband ein Teilverband, aber nicht umgekehrt.

Hier ist eine der wenigen Stellen, wo man den Unterschied in der Betrachtungsweise merkt: Für Verbände als Ordnungsstrukturen sind alle Teilverbände Unterstrukturen, für Verbände als algebraische Strukturen sind nur die Unterverbände Unterstrukturen.

Man geht weder bei Teilverbänden noch bei Unterverbänden davon aus, dass die neutralen Elemente in der Unterstruktur erhalten bleiben. Sonst muss man ausdrücklich von einem Verband mit $0$ und reden.

Ideale und Filter

→ Hauptartikel: Ideal (Mathematik), Primideal und Maximales Ideal

→ Hauptartikel: Filter (Mathematik) und Ultrafilter

Ein Ideal ist ein Unterverband eines Verbandes , der zusätzlich folgende Bedingung erfüllt: sind $a\in I$ und $x\in V$ , dann ist $a\wedge x\in I$ . (Die Definition entspricht also formal der Definition, die man in einem Ring erwartet).

Bezüglich der Halbordnung auf gilt aber $a\wedge x\leq a$ . Daher kann man die Definition auch so interpretieren:

Ein Ideal ist ein Unterverband, der zusammen mit einem Element auch alle Elemente von enthält, die kleiner als sind.

Filter werden dual zu Idealen definiert:

Ein Filter ist ein Unterverband, der zusammen mit einem Element auch alle Elemente von enthält, die größer als sind.

Homomorphismen

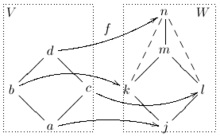
Zum Beispiel ist die hier dargestellte monotone Abbildung zwischen den Verbänden und kein Homomorphismus, da $f(b\vee c)=n$ , aber $f(b)\vee f(c)=m$ . Außerdem ist aus demselben Grund das Bild $f(V)=\{j,k,l,n\}$ zwar ein Verband (mit $k\vee l=n$ ), aber kein Unterverband von .

Sind $(V,\vee ,\wedge )$ und $(W,\vee ,\wedge )$ zwei Verbände und $f\colon \,V\to W$ eine Funktion, sodass für alle a,b aus gilt

$f(a\vee b)=f(a)\vee f(b),$
$f(a\wedge b)=f(a)\wedge f(b),$

dann heißt Verbandshomomorphismus. Ist zusätzlich bijektiv, dann heißt Verbandsisomorphismus und die Verbände und sind isomorph.

Falls $(V,\vee ,\wedge )$ und $(W,\vee ,\wedge )$ vollständig sind und $f\colon \,V\to W$ sogar

$f\left(\bigvee T\right)=\bigvee \{f(a)\mid a\in T\},$
$f\left(\bigwedge T\right)=\bigwedge \{f(a)\mid a\in T\}$

für alle $T\subseteq V$ erfüllt, nennt man einen vollständigen Verbandshomomorphismus. Jeder vollständige Verbandshomomorphismus ist offensichtlich auch ein Verbandshomomorphismus.

Die Klasse aller Verbände bildet mit diesen Homomorphismen jeweils eine Kategorie.

Ein Verbandshomomorphismus ist gleichzeitig ein Ordnungshomomorphismus, d.h. eine isotone Abbildung:

aus $a\leq b$ folgt $f(a)\leq f(b).$

Jedoch ist nicht jede isotone Abbildung zwischen Verbänden ein Verbandshomomorphismus.

In beschränkten Verbänden gilt: Die Menge der Elemente von die durch einen Verbandshomomorphismus auf das Nullelement des Bildes abgebildet werden, bilden ein Ideal von und dual, die Menge der Elemente, die auf das Einselement abgebildet werden, bilden einen Filter.

Weitere Beispiele für Verbände

Total geordnete Mengen

Jede total geordnete Menge ist ein distributiver Verband mit den Verknüpfungen Maximum und Minimum. Insbesondere gilt für alle , , aus :

$\max(a,\min(b,c))=\min(\max(a,b),\max(a,c))$ ,
$\min(a,\max(b,c))=\max(\min(a,b),\min(a,c))$ .

Nur im Fall einer ein- oder zweielementigen Menge ist der Verband komplementär.

Beispiele für die übrigen Eigenschaften:

Das abgeschlossene reelle Intervall und die erweiterte reelle Gerade ( $\mathbb {R}$ mit $\infty$ und $-\infty$ ) sind jeweils vollständige distributive Verbände (und damit beschränkt).
Das offene reelle Intervall , die Mengen $\mathbb {R}$ , $\mathbb {Q}$ und $\mathbb {Z}$ sind jeweils unvollständige unbeschränkte distributive Verbände.
Das rationale Intervall $[0,1]\cap \mathbb {Q}$ ist ein unvollständiger beschränkter distributiver Verband.
Die Menge $\mathbb {N} _{0}$ ist ein unvollständiger distributiver Verband mit Nullelement $0$ .

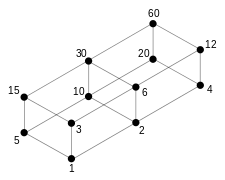
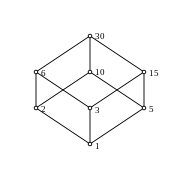
Teilerverbände

Betrachtet man für eine natürliche Zahl die Menge aller Teiler von , dann ist $(T,\operatorname {ggT} ,\operatorname {kgV} )$ ein vollständiger distributiver Verband mit Einselement (neutralem Element für ggT) und Nullelement (neutralem Element für kgV). Er heißt Teilerverband von . Die Absorptionsgesetze und Distributivgesetze für ggT und kgV folgen dabei z.B. mit der Primfaktorzerlegung aus den Eigenschaften von max und min, man kann sie aber auch durch Teilbarkeitsbetrachtungen herleiten. Der Verband ist genau dann komplementär (und damit boolesch), wenn quadratfrei ist, d.h. wenn keine Quadratzahl $\neq 1$ als Teiler hat. Die Halbordnung auf ist die Teiler-Relation:

$a\leq b$ genau dann, wenn (genau dann, wenn $\operatorname {ggT} (a,b)=a$ ).

Beispiele für Teilerverbände

T₂ ist Boolesche Algebra (und lineare Ordnung)

T₄ ist lineare Ordnung

T₆ ist eine Boolesche Algebra

T₁₂ ist nicht komplementär

T₃₀ ist eine Boolesche Algebra

$(\mathbb {N} _{0},\operatorname {kgV} ,\operatorname {ggT} )$ ist beschränkt und distributiv, aber nicht komplementär. Jeder Teilerverband ist als Unterverband enthalten

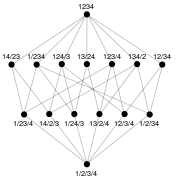
Teilmengenverbände

Für eine Menge bildet die Potenzmenge ${\mathcal {P}}(M)$ mit den Verknüpfungen Vereinigung $\cup$ und Durchschnitt $\cap$ einen algebraischen booleschen Verband mit Nullelement $\emptyset$ (neutrales Element bezüglich $\cup$ ) und Einselement (neutrales Element bezüglich $\cap$ ) sowie Komplement $A^{c}=M\setminus A$ für alle $A\in {\mathcal {P}}(M)$ . Er heißt Potenzmengen- oder Teilmengenverband von . Die Halbordnung auf $({\mathcal {P}}(M),\cup ,\cap )$ ist die Mengeninklusion:

$A\leq B,$ falls $A\subseteq B$ (oder äquivalent dazu $A\cap B=A$ )

(Trägermengen von) Unterverbände(n) von $({\mathcal {P}}(M),\cup ,\cap )$ heißen Mengenverbände (zwischen den Verbänden und ihren Trägermengen wird oft nicht unterschieden). Diese Verbände sind immer distributiv, müssen jedoch weder vollständig sein, noch neutrale Elemente oder Komplemente haben. (Ein Beispiel dafür ist der Verband der rechts-unendlichen reellen Intervalle $[a,\infty )$ mit aus $\mathbb {R}$ , der isomorph zum Verband der reellen Zahlen ist.)

Unterstrukturenverbände von algebraischen Strukturen, Untergruppenverbände

Für eine Gruppe $(G,{\ast })$ bildet die Menge aller Untergruppen von einen algebraischen (im Allgemeinen nicht modularen und damit auch nicht distributiven) Verband mit den Verknüpfungen Erzeugnis der Vereinigung und Durchschnitt. Er heißt Untergruppenverband von .

Beispielsweise ist der Untergruppenverband der kleinschen Vierergruppe, der gerade dem Verband $M_{3}$ entspricht, nicht-distributiv, aber modular.

Ebenso bilden

die normalen Untergruppen einer Gruppe,
die Untergruppen einer abelschen Gruppe,
die Unterringe eines Ringes,
die Unterkörper eines Körpers,
die Untermoduln eines Moduls,
die Ideale eines Ringes

mit analogen Verknüpfungen einen modularen algebraischen Verband. Die Untergruppen einer beliebigen Gruppe und die Unterverbände eines beliebigen Verbands ergeben zwar immer einen algebraischen Verband, dieser muss aber nicht modular sein.

Ganz allgemein bilden die Unterstrukturen einer algebraischen Struktur stets einen algebraischen Verband (wobei auch die leere Menge als Unterstruktur betrachtet wird, falls der mengentheoretische Durchschnitt – also das Infimum bezüglich der Mengeninklusion – von der Menge aller Unterstrukturen leer ist).

Insbesondere ist ein Verband genau dann algebraisch, wenn er isomorph ist zum Verband der Unterstrukturen einer algebraischen Struktur (daher auch der Name algebraischer Verband).

Schränkt man die Menge der Untergruppen auf Obergruppen einer festen Untergruppe ein, so bilden alle diese Zwischengruppen $\{V\colon U\leq V\leq G\}$ auch einen beschränkten Verband. Analog dazu gibt es Verbände von Zwischenringen, Zwischenkörpern, Zwischenmoduln, Zwischenidealen.

Besonderes Interesse hat man am Untergruppenverband der Galoisgruppe einer galoisschen Körpererweiterung L/K , denn er ist isomorph zum dualen Zwischenkörperverband von L/K .

Basierend auf einem Artikel in:

Wikipedia.de