Vollständige Induktion

Die vollständige Induktion ist eine mathematische Beweismethode, nach der eine Aussage für alle natürlichen Zahlen bewiesen wird. Da es sich um unendlich viele Zahlen handelt, kann solch ein Beweis nicht für alle Einzelfälle durchgeführt werden. Er wird daher in zwei Etappen durchgeführt: als Induktionsanfang für eine kleinste Zahl, für die man die Aussage zeigen will (meist 1 oder 0), und als Induktionsschritt, der aus der Aussage für eine variable Zahl die entsprechende Aussage für die nächste Zahl logisch ableitet. Dieses Beweisverfahren ist von grundlegender Bedeutung für die Arithmetik und Mengenlehre und damit für alle Gebiete der Mathematik.

Veranschaulichung

Konkrete Induktionsschritte

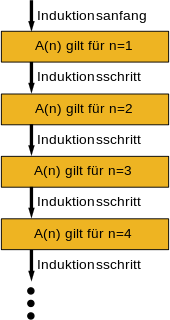
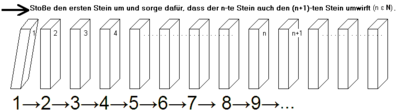
Die vollständige Induktion erfasst durch den variablen Induktionsschritt beliebig viele Schritte, die man von 1 aus konkret durchführen kann. Das verdeutlicht die Grafik links. Diese Methode ist mit dem Dominoeffekt vergleichbar: Wenn der erste Dominostein fällt und durch jeden fallenden Dominostein der nächste umgestoßen wird, so wird schließlich jeder Dominostein der unendlich lang gedachten Kette irgendwann umfallen.

Vollständige Induktion als Dominoeffekt mit unendlich vielen Steinen

Etymologie und Geschichte

Die Bezeichnung Induktion leitet sich ab von lat. inductio, wörtlich „Hineinführung“. Der Zusatz vollständig signalisiert, dass es sich hier im Gegensatz zur philosophischen Induktion, die aus Spezialfällen ein allgemeines Gesetz erschließt und kein exaktes Schlussverfahren ist, um ein anerkanntes deduktives Beweisverfahren handelt.

Das Induktionsprinzip steckt latent bereits in der von Euklid überlieferten pythagoreischen Zahlendefinition: „Zahl ist die aus Einheiten zusammengesetzte Menge.“ Euklid führte aber noch keine Induktionsbeweise, sondern begnügte sich mit intuitiven, exemplarischen Induktionen, die sich aber vervollständigen lassen. Auch andere bedeutende Mathematiker der Antike und des Mittelalters hatten noch kein Bedürfnis nach präzisen Induktionsbeweisen. Vereinzelte Ausnahmen im hebräischen und arabischen Sprachraum blieben ohne Nachfolge.

Lange galt ein Beweis von Franciscus Maurolicus von 1575 als älteste explizite vollständige Induktion (unten ausgeführt) Er erörterte aber das allgemeine Beweisverfahren noch nicht. Erst Blaise Pascal thematisierte das Induktionsprizip mit Induktionsanfang und Induktionsschritt in seinem Traité du triangle arithmétique von 1654. Zur Verbreitung von Induktionsbeweisen trug ab 1686 Jakob Bernoulli wesentlich bei.

Das Beweisverfahren wurde dann 1838 von Augustus De Morgan erstmals als Induktion oder sukzessive Induktion bezeichnet. 1888 prägte schließlich Richard Dedekind in seiner Schrift Was sind und was sollen die Zahlen? den Begriff vollständige Induktion. Über dieses Werk aus der Gründerzeit der Mengenlehre wurde sie zum allgemein bekannten, etablierten Beweisprinzip, auf das seither kein Zweig der Mathematik mehr verzichten kann. Ein Jahr später, 1889, formulierte Giuseppe Peano den ersten formalisierten Kalkül für die natürlichen Zahlen mit einem Induktionsaxiom, aus dem das Beweisschema der vollständigen Induktion herleitbar ist. Er zeigte mit formaler Strenge, dass aus seinen Zahlaxiomen, zu denen das Induktionsaxiom gehört, die ganze Arithmetik bis hin zu den reellen Zahlen ableitbar ist. Dadurch machte er die fundamentale Bedeutung und die Leistungskraft der Induktion voll bewusst.

Definition

Seit Richard Dedekind ist die vollständige Induktion folgendermaßen festgelegt:

Um zu beweisen, dass ein Satz für alle natürlichen Zahlen n ≥ m gilt, genügt es zu zeigen, dass er für n = m gilt und dass aus der Gültigkeit des Satzes für eine Zahl n ≥ m stets seine Gültigkeit auch für die folgende Zahl n + 1 folgt.

Als formale Schlussregel mit Ableitungsoperator $\vdash$ lautet die vollständige Induktion für eine Aussage A(n) und eine natürliche Zahl :

$A(m) {,}\quad \forall n \in \N\colon(n \geq m \and A(n)\Rightarrow A(n+1))\ \vdash\ \forall n \in \N \colon (n \geq m \Rightarrow A(n))$

Diese Schlussregel ist eine kompakte Formulierung des Beweisschemas der vollständigen Induktion, das didaktisch etwas ausführlicher formuliert werden kann:

Soll die Formel A(n) für alle natürlichen Zahlen n ≥ m bewiesen werden, dann genügen dazu zwei Beweisschritte:

1. der Induktionsanfang: der Beweis von A(m)

2. der Induktionsschritt: der Beweis der Induktionsbehauptung A(n + 1) mit Hilfe der Induktionsvoraussetzung A(n) und n ≥ m.

Nach obiger Schlussregel (dem eigentlichen Induktionsschluss) folgt dann die Gültigkeit der Formel A(n) für alle natürlichen Zahlen n ≥ m.

Meist ist m = 0 oder m = 1. m > 1 ist jedoch möglich.

Da die Aussage A(n) für n ≥ m gleichwertig ist zur Aussage A(n + m) für n ≥ 0, lässt sich Dedekinds Induktion auf die vollständige Induktion von 0 aus zurückführen:

$A(0) {,}\quad \forall n \in \N\colon (A(n)\Rightarrow A(n+1))\ \vdash\ \forall n \in \N \colon A(n)$

Herleitung

Die vollständige Induktion kann aus Axiomen für die natürlichen Zahlen hergeleitet werden. Am bekanntesten ist die Ableitung aus dem fünften Peano-Axiom, dem sogenannten Induktionsaxiom, das folgendermaßen lautet: Ist $\,0$ ein Element von $\,K$ und ist mit $\,n$ aus $\,K$ stets auch $\,n+1$ aus $\,K$ , dann ist $\N$ eine Teilmenge von $\,K$ . Wählt man in diesem Axiom für $\,K$ die Menge aller natürlicher Zahlen $\,n$ , die die Aussage $\,A(n)$ erfüllen, so ergibt sich die vollständige Induktion mit Induktionsanfang $\,A(0)$ .

Auch in anderen Konzepten der natürlichen Zahlen sind die Peano-Axiome und damit auch das Beweisverfahren der vollständigen Induktion herleitbar, zum Beispiel bei der Definition der natürlichen Zahlen

als von 1 erzeugte geordnete Halbgruppe, die der zitierten pythagoreischen Zahlendefinition entspricht
als frei von 1 erzeugtes Monoid, das von der Addition der Zahlen ausgeht
als Algebra mit Nachfolger-Abbildung, die Dedekinds Zahlendefinition entspricht
als kleinste induktive Menge, nämlich als kleinste Menge, die das Unendlichkeitsaxiom erfüllt, wie es in der Mengenlehre üblich ist
als Klasse der endlichen Ordinalzahlen, die nur eine allgemeine Mengenlehre ohne Unendlichkeitsaxiom voraussetzt

Beispiele

Peano bewies 1889 mit vollständiger Induktion die grundlegenden Rechenregeln für die Addition und Multiplikation: das Assoziativgesetz, Kommutativgesetz und Distributivgesetz.

Summe ungerader Zahlen (Maurolicus 1575)

Die schrittweise Berechnung der Summe der ersten ungeraden Zahlen legt die Vermutung nahe: Die Summe aller ungeraden Zahlen von bis 2n-1 ist gleich dem Quadrat von :

1 = 1

1 + 3 = 4

1 + 3 + 5 = 9

1 + 3 + 5 + 7 = 16

Der allgemeine Satz lautet: $\textstyle \sum\limits^n_{i=1} (2i-1) = n^2$ . Ihn bewies Maurolicus 1575 mit vollständiger Induktion. Ein Beweis mit heute geläufigen Rechenregeln liest sich folgendermaßen:

Der Induktionsanfang gilt wegen $\textstyle \sum\limits^1_{i=1} (2i-1) = 2\cdot 1-1 = 1 =1^2$ .

Beim Induktionsschritt ist zu zeigen: Wenn $\textstyle \sum\limits^n_{i=1} (2i-1) = n^2$ , dann $\textstyle \sum\limits^{n+1}_{i=1} (2i-1) = (n+1)^2$ . Er ergibt sich über folgende Gleichungskette, bei der in der zweiten Umformung die Induktionsvoraussetzung angewandt wird:

$\begin{align} \sum^{n+1}_{i=1} (2i-1) \;&=\;\; \left( \sum^n_{i=1} (2i-1) \right) + (2(n+1)-1)\\[.3em] &\overset{\text{IVor.}}{=}\; n^2 + 2(n+1)-1 = n^2 + 2n +1 = (n+1)^2 \end{align}$ .

Gaußsche Summenformel

→ Hauptartikel: Gaußsche Summenformel

Die Gaußsche Summenformel lautet: Für alle natürliche Zahlen $n \geq 1$ gilt

$\sum^n_{k=1} k = 1+2+\cdots+n = \frac{n(n+1)}{2}$

Auch sie kann durch vollständige Induktion bewiesen werden. Der Induktionsanfang ergibt sich unmittelbar:

$\sum^1_{k=1} k = 1 = \frac{1(1+1)}{2}$

Der Induktionsschritt wird über folgende Gleichungskette gewonnen, bei der die Induktionsvoraussetzung mit der zweiten Umformung verwendet wird:

$\begin{align}\sum^{n+1}_{k=1} k = \left( \sum^n_{k=1} k \right) + (n+1) = \frac{n(n+1)}{2}+(n+1)\\ =\frac{n(n+1)+2(n+1)}{2} = \frac{(n+1)(n+2)}{2}\end{align}$

Bernoullische Ungleichung

Die Bernoullische Ungleichung lautet für reelle Zahlen $\,x$ mit $x+1 \geq 0$ und natürliche Zahlen $n \geq 0$

$(1+x)^n \geq 1+nx$ .

Der Induktionsanfang gilt hier wegen $(1+x)^0 = 1 \geq 1$ . Den Induktionsschritt gewinnt man über folgende Ableitung, die im zweiten Schritt die Induktionsvoraussetzung verwendet, wobei obige Bedingung für $\,x$ dafür sorgt, dass der Term nicht negativ wird:

$\begin{align}(1+x)^{n+1} = (1+x)^n \cdot (1+x) \geq (1+nx)\cdot(1+x) = \\ = 1 + x + nx + nx^2 \geq 1 + x + nx = 1 + (n+1)x\end{align}$

Induktion mit beliebigem Anfang

Induktionsbeweis der Ungleichung $2^n\ge n^2$ für natürliche Zahlen $n\ge 4$ :

Der Induktionsanfang für $\,n = 4$ ergibt sich mit $2^{4}=16\ge 16 = 4^2$ .

Der Induktionsschritt gilt aufgrund folgender Ableitung, die im zweiten Schritt die Induktionsvoraussetzung und im vierten und sechsten Schritt die Voraussetzung $n\ge 4$ anwendet:

$2^{n+1}=2\cdot 2^n\ge 2\cdot n^2 =n^2+n\cdot n \ge n^2+4n = n^2+2n+2n \ge n^2+2n+2\cdot4 \ge n^2+2n+1=(n+1)^2$ .

Die endlich vielen Fälle, die solch ein allgemeinerer Induktionsbeweis nicht abdeckt, können einzeln untersucht werden. Im Beispiel ist die Ungleichung für $\,n=3$ offenbar falsch.

Induktion mit mehreren Vorgängern

In manchen Induktionsbeweisen benötigt man eine Induktionsvoraussetzung für mehrere Vorgänger; der Induktionsanfang ist dann für mehrere Startwerte durchzuführen. Ist zur Ableitung einer Formel etwa die Induktionsvoraussetzung für n und n−1 nötig, dann ist ein Induktionsanfang für zwei aufeinander folgende Zahlen, also etwa 0 und 1, erforderlich. Als Induktionsvoraussetzung kann auch die Aussage für alle Zahlen zwischen dem Startwert und n dienen. Ein Beispiel ist der Beweis, dass jede natürliche Zahl $n\geq 2$ einen Primzahl-Teiler hat:

Induktionsanfang: 2 ist durch die Primzahl 2 teilbar. Induktionsschritt: Die Aussage sei für alle $\,m$ mit $2\leq m \leq n$ erfüllt. Ist nun $\,n+1$ eine Primzahl, so ist $\,n+1$ selbst der gesuchte Teiler. Ist $\,n+1$ keine Primzahl, so gibt es zwei Zahlen $\,a, b$ mit $a\cdot b=n+1$ und $2\leq a,b\leq n$ . Beide Zahlen erfüllen also die Induktionsvoraussetzung. Insbesondere besitzt $\,a$ einen Primzahl-Teiler $\,p$ . $\,p$ teilt auch $\,n+1$ und ist somit ein Primzahl-Teiler von $\,n+1$ .

Induktionsvarianten

Ein Induktionsbeweis ist auch für Aussagen über alle ganzen Zahlen (positiv und negativ) möglich. Man beginnt dazu mit einem beliebigen Induktionsanfang, beweist den positiven Induktionsschritt von n nach n+1 und anschließend den Induktionsschritt in negativer Richtung von n nach n−1. Beim Induktionsanfang 0 kann man den zweiten Induktionsschritt auch von n nach −n zeigen.

Augustin-Louis Cauchy führte 1821 eine Induktionsvariante ein, bei der der vorwärts gerichtete Induktionsschritt Sprünge macht (etwa von n nach 2n) und die entstehenden Lücken anschließend durch einen rückwärts gerichteten Induktionsschritt von n nach n−1 gefüllt werden.

Die vollständige Induktion ist von natürlichen Zahlen verallgemeinerbar auf Ordinalzahlen. Bei Ordinalzahlen, die größer als die natürlichen Zahlen sind, spricht man dann von transfiniter Induktion.

Die Induktion ist auch übertragbar auf sogenannte fundierte Mengen, die eine der Zahlenordnung vergleichbare Ordnungsstruktur aufweisen; hier spricht man zuweilen von struktureller Induktion.

Rekursive oder induktive Definition

Dierekursive Definition – früher auch induktive Definition genannt – ist ein der vollständigen Induktion analoges Verfahren, bei der ein Term durch einen Rekursionsanfang und einen Rekursionsschritt definiert wird. Ein konstruktiver Beweis mit vollständiger Induktion kann eine rekursive Berechnung ersparen. Zum Beispiel erspart die Gaußsche Summenformel eine rekursive Berechnung der Summe $\textstyle \sum^n_{k=1} k$ über den Rekursionsanfang $\textstyle \sum^1_{k=1} k=1$ und den Rekursionsschritt $\textstyle \sum^{n+1}_{k=1} k=\sum^{n}_{k=1}k+n+1$ .

Die rekursive Definition hat wie die Induktion allerlei differenzierte Varianten.

Basierend auf einem Artikel in:

Wikipedia.de