Fibonacci-Folge

Die Fibonacci-Folge ist die unendliche Folge natürlicher Zahlen, die (ursprünglich) mit zweimal der Zahl 1 beginnt oder (häufig, in moderner Schreibweise) zusätzlich mit einer führenden Zahl 0 versehen ist. Im Anschluss ergibt jeweils die Summe zweier aufeinanderfolgender Zahlen die unmittelbar danach folgende Zahl:
|
|
Die darin enthaltenen Zahlen heißen Fibonacci-Zahlen. Benannt ist die Folge nach Leonardo Fibonacci, der damit im Jahr 1202 das Wachstum einer Kaninchenpopulation beschrieb. Die Folge war aber schon in der Antike sowohl den Griechen als auch den Indern bekannt.
Weitere Untersuchungen zeigten, dass die Fibonacci-Folge auch noch zahlreiche andere Wachstumsvorgänge in der Natur beschreibt. Es scheint, als sei sie eine Art Wachstumsmuster in der Natur.
Die Fibonacci-Zahlen weisen einige bemerkenswerte mathematische Besonderheiten auf:
- Aufgrund der Beziehung zur vorherigen und zur folgenden Zahl scheint Wachstum in der Natur einem Additionsgesetz zu folgen.
- Die Fibonacci-Folge steht in einem unmittelbaren Zusammenhang zum Goldenen Schnitt. Je weiter man in der Folge fortschreitet, desto mehr nähert sich der Quotient aufeinanderfolgender Zahlen dem Goldenen Schnitt (1,618033…) an (beispielsweise 13:8 = 1,6250; 21:13 ≈ 1,6154; 34:21 ≈ 1,6190; 55:34 ≈ 1,6176; etc.).
- Diese Annäherung ist alternierend, d.h. die Quotienten sind abwechselnd kleiner und größer als der Goldene Schnitt.
Definition der Fibonacci-Folge
Die Fibonacci-Folge
ist durch das rekursive
Bildungsgesetz
für
mit den Anfangswerten
definiert.[1] Das bedeutet in Worten:
- Für die beiden ersten Zahlen wird der Wert
vorgegeben.
- Jede weitere Zahl ist die Summe ihrer beiden Vorgänger in der Folge.
Daraus ergibt sich:
-
n fn n fn n fn n fn n fn 1 1 11 89 21 10 946 31 1 346 269 41 165 580 141 2 1 12 144 22 17 711 32 2 178 309 42 267 914 296 3 2 13 233 23 28 657 33 3 524 578 43 433 494 437 4 3 14 377 24 46 368 34 5 702 887 44 701 408 733 5 5 15 610 25 75 025 35 9 227 465 45 1 134 903 170 6 8 16 987 26 121 393 36 14 930 352 46 1 836 311 903 7 13 17 1 597 27 196 418 37 24 157 817 47 2 971 215 073 8 21 18 2 584 28 317 811 38 39 088 169 48 4 807 526 976 9 34 19 4 181 29 514 229 39 63 245 986 49 7 778 742 049 10 55 20 6 765 30 832 040 40 102 334 155 50 12 586 269 025
Aus der Forderung, dass die Rekursion
auch für ganze Zahlen
gelten soll, erhält man eine eindeutige Fortsetzung auf den Index 0 und auf
negative Indizes. Es gilt:
für alle
Die so erweiterte Fibonacci-Folge lautet dann
-
13 −8 5 −3 2 −1 1 0 1 1 2 3 5 8 13
und heißt Folge der negaFibonacci-Zahlen.
Darüber hinaus ist eine Verallgemeinerung der Fibonacci-Zahlen auf komplexe Zahlen, proendliche Zahlen und auf Vektorräume möglich.
Eigenschaften
Zu den zahlreichen bemerkenswerten Eigenschaften der Fibonacci-Zahlen gehört beispielsweise, dass sie dem Benfordschen Gesetz genügen.
Verwandtschaft mit dem Goldenen Schnitt
Wie von Johannes
Kepler festgestellt wurde, nähert sich der Quotient
zweier aufeinanderfolgender Fibonacci-Zahlen dem Goldenen Schnitt
an. Dies folgt unmittelbar aus der Näherungsformel
für große
:
Diese Quotienten zweier aufeinanderfolgender Fibonacci-Zahlen haben eine bemerkenswerte Kettenbruchdarstellung:
mit der -Notation
aus endliche
Kettenbrüche.
Da diese Quotienten im Grenzwert gegen den goldenen Schnitt konvergieren, lässt sich dieser als der unendliche periodische Kettenbruch:
darstellen. Die Zahl
ist irrational.
Das bedeutet, dass sie sich nicht durch ein Verhältnis zweier ganzer Zahlen
darstellen lässt. Am besten lässt sich
durch Quotienten zweier aufeinanderfolgender Fibonacci-Zahlen approximieren.
Dies gilt auch für verallgemeinerte Fibonaccifolgen, bei denen
und
beliebige natürliche Zahlen annehmen.
Beziehungen zwischen den Folgegliedern
mit der Lucas-Folge
(mit
), insbesondere:
(Identität von Catalan)
(Identität von Cassini, Spezialfall der Catalan-Identität)
(Identität von d’Ocagne)
- Je zwei benachbarte Fibonaccizahlen sind teilerfremd, d.h.
.
; für
gilt auch die Umkehrung. Insbesondere kann
für
nur dann eine Primzahl sein, wenn
eine Primzahl ist.
(Genau jede dritte Fibonacci-Zahl ist durch 2 teilbar.)
(Genau jede vierte Fibonacci-Zahl ist durch 3 teilbar.)
(Genau jede sechste Fibonacci-Zahl ist durch 4 teilbar.)
(Genau jede fünfte Fibonacci-Zahl ist durch 5 teilbar.)
(Genau jede achte Fibonacci-Zahl ist durch 7 teilbar.)
(Genau jede zwölfte Fibonacci-Zahl ist durch 16 teilbar.)
- Für die Teilbarkeit durch Primzahlen
gilt unter Verwendung des Jacobi-Symbols:
Es gibt noch zahlreiche weitere derartige Formeln.
Reziproke Reihe
- Der Grenzwert der absolut konvergierenden reziproken Reihe der
Fibonacci-Zahlen
- ist irrational (André-Jeannin; 1989).
- Zudem zeigte Good (1974) und Hoggatt (1976):
.
Zeckendorf-Theorem
Das nach Edouard
Zeckendorf benannte Zeckendorf-Theorem besagt, dass jede natürliche Zahl
eindeutig als Summe voneinander verschiedener, nicht direkt aufeinanderfolgender
Fibonacci-Zahlen
geschrieben werden kann. Das heißt, es gibt für jedes
eine eindeutige Darstellung der Form
mit
und
für alle
.
Die entstehende Folge
von Nullen und Einsen wird Zeckendorf-Sequenz
genannt. Sehr eng hängt damit der Fibonacci-Kode
zusammen.
Berechnung
Formel von Moivre-Binet
.png)
Das explizite Bildungsgesetz für die Glieder der Fibonacci-Folge wurde unabhängig voneinander von den französischen Mathematikern Abraham de Moivre im Jahr 1718 und Jacques Philippe Marie Binet im Jahr 1843 entdeckt. Dazwischen war sie aber auch den Mathematikern Leonhard Euler und Daniel Bernoulli bekannt, Letzterer lieferte 1728 auch den vermutlich ersten Beweis.[13]
Die Fibonacci-Zahlen lassen sich direkt mittels
berechnen, wobei
die beiden Lösungen der charakteristischen
Gleichung
sind. Mit
ist explizit:
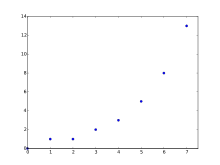
Bemerkenswert ist das Zusammenspiel zweier irrationaler Zahlen
und
,
das zu einem ganzzahligen Ergebnis führt. Die Abbildung zeigt die beiden Folgen
und
und
als ihre Differenz.
Näherungsformel für große Zahlen
Der Einfluss von
geht rasch gegen Null, bspw. ist
.
Das kann man verwenden, um die Berechnung abzukürzen, indem man den Term für
genügend große
ignoriert und das Ergebnis zur
nächsten natürlichen Zahl rundet:
(Gaußsche Rundungsklammer
)
Tatsächlich geht das schon für .
Induktiver Beweis
Einer der einfachsten Beweise gelingt induktiv. Wegen
und
ist der Induktionsanfang erfüllt. Angenommen, die Formel gelte für alle Werte
von
bis
(starke
Induktionsvoraussetzung). Wir zeigen, dass sie dann notwendigerweise auch
für
gelten muss:
Dabei haben wir benutzt, dass
und
der charakteristischen Gleichung
genügen.
Nach dem Prinzip der vollständigen Induktion muss nun die Formel für alle
gelten.
Herleitung der Formel von Moivre-Binet
Die Formel von Binet kann mit Matrizenrechnung und dem Eigenwertproblem in der linearen Algebra hergeleitet werden mittels folgendem Ansatz:
Nun transformiert man die Matrix
in eine Diagonalmatrix
durch Betrachtung als Eigenwertproblem.
Es gilt ,
wobei
die Matrix der Eigenvektoren und
die Diagonalmatrix mit den Eigenwerten ist. Damit folgt:
Herleitung mittels Differenzengleichung
Eine andere Herleitungsmöglichkeit folgt aus der Theorie der linearen Differenzengleichungen:
Sei
eine geometrische
Folge, so ergibt sich:
Wenn also
so gewählt wird, dass die charakteristische Gleichung
erfüllt ist (also
oder
),
wird
,
d.h.,
erfüllt die Fibonacci-Rekursion mit dem Rekursionsanfang
und
.
Die rekursive Folge ,
,
hat die explizite Darstellung
.
Ebenso
,
,
.
Mit
und
genügt wegen der Superpositionseigenschaft
auch jede Linearkombination
der Fibonacci-Rekursion
.
Mit Hilfe eines linearen Gleichungssystems ergibt sich
und
,
damit
und
.
Folglich ergibt sich explizit
.
Für
ergibt sich
und
,
d.h. die klassische Lucas-Folge
mit explizit
.
Herleitung mittels z-Transformation
Da Differenzengleichungen sehr elegant mittels z-Transformation beschrieben werden können, kann man die z-Transformation auch zur Herleitung der expliziten Formel für Fibonacci-Zahlen einsetzen. Im Artikel Einsatz der z-Transformation zur Bestimmung expliziter Formeln von Rekursionsvorschriften wird die allgemeine Vorgehensweise beschrieben und dann am Beispiel der Fibonacci-Zahlenfolge erläutert.
Alternierende Näherung
Die Quotienten aufeinander folgender Glieder der Fibonacci-Folge sind abwechselnd kleiner und größer als der Goldene Schnitt:
| Herleitung |
| .
Mithilfe der Formel von Moivre-Binet lässt sich eine einfach Herleitung
angeben. Denn für die Zahlen
Die Ungleichungen (1) und (2) ergeben zusammen die Behauptung. |
Die Differenz dieser oberen und unteren Schranke von
konvergiert für wachsende
rasch gegen Null, denn:
;
bei der Vereinfachung des Zählers wurde die Identität
von Cassini nebst
verwendet.
Erzeugende Funktion
Eine erzeugende Funktion der Fibonacci-Zahlen ist
Die auf der linken Seite stehende Potenzreihe
konvergiert für .
Über die angegebene Partialbruchzerlegung
erhält man wiederum die Formel von de Moivre-Binet.
| Herleitung der erzeugenden Funktion |
|
Für
Die Rekursionsbedigung
Nach Division durch das Polynom |
Mit einer geeigneten erzeugenden Funktion lässt sich ein Zusammenhang zwischen den Fibonacci-Zahlen und den Binomialkoeffizienten darstellen:
.
Wegen
für
und
kann auch ohne Gaußklammern geschrieben werden:
.
| Herleitung |
|
Die erzeugende Funktion kann auch geschrieben werden:
für dem Betrage nach hinreichend kleine
Gleichsetzen ergibt:
bei der Umformung wurden der Binomische
Lehrsatz und die Umsummierung Koeffizientenvergleich ergibt den angegebenen Zusammenhang. |
Die Schreibweise
für die erzeugende Funktion erlaubt auch die Darstellung:
| Herleitung |
|
In der Darstellung von Die
für |
Darstellung mit Matrizen
Die Fibonacci-Zahlen tauchen auch als Einträge der Potenzen der Matrix
auf:
Aus der Relation
ergibt sich beispielsweise die erste oben angegebene Formel für
.
beschreibt zugleich die Summationsvorschrift der Fibonacci-Folge, denn ihr
Produkt mit einem Paar aufeinanderfolgender Fibonacci-Zahlen (als Spaltenmatrix
geschrieben) ergibt das nächste Paar; entsprechend erzeugt
das
-te
Paar aus dem Startpaar
.
Dies und die Tatsache, dass die Eigenwerte von
gerade der Goldene
Schnitt und dessen Kehrwert (letzterer mit negativem Vorzeichen) sind,
führen wieder auf die oben genannte Formel von Binet.
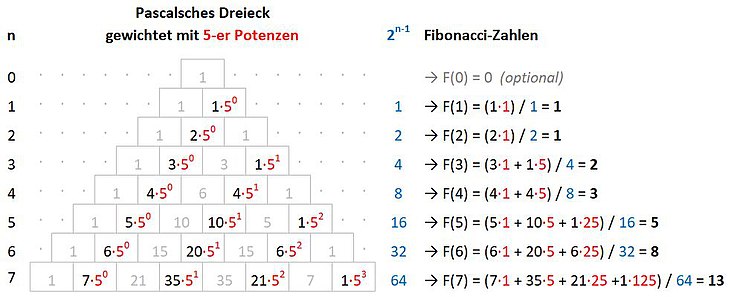
Verwandtschaft mit dem Pascalschen Dreieck
Die Fibonacci-Zahlen können mithilfe des Pascalschen
Dreiecks beschrieben werden. Um die n-te Fibonacci-Zahl zu bestimmen, nimmt
man aus der n-ten Zeile des Pascalschen
Dreiecks jede zweite Zahl und gewichtet sie mit der entsprechenden
Fünfer-Potenz – anfangend mit 0 in aufsteigender Reihenfolge, d.h. ,
,
usw. Anschließend addiert man diese gewichteten Elemente zusammen und dividiert
durch
.
Das Bild unten veranschaulicht die Berechnung der ersten sieben
Fibonacci-Zahlen aus dem Pascalschen
Dreieck. Zum leichteren Verständnis sind die nicht benutzten Elemente des
Pascalschen Dreiecks im Bild ausgegraut, die Gewichtung mit den
aufsteigenden Fünfer-Potenzen rot und die Exponenten
cyan hervorgehoben.
| Herleitung |
|
Ausgehend von der expliziten Formel für die Fibonacci-Zahlen (s. Formel von Moivre-Binet weiter oben in diesem Artikel) kann man zunächst den Term Für die Differenz unter dem Summenzeichen gilt: so dass man die Summe auf ungerade Der Vergleicht man die unter dem Summenzeichen verbliebenen Binomialkoeffizienten mit denen im Pascalschen Dreieck, erkennt man, dass es sich dabei um jeden zweiten Koeffizienten in der entsprechenden Zeile des Dreiecks handelt (wie es im Bild oben visualisiert ist). Man kann die Formel also auch als Mit der Bezeichnung |
Verallgemeinerungen
Die klassische („kanonische“) Fibonacci-Folge ist durch drei Kriterien charakterisiert:
- Eine lineare Iteration, welche die beiden vorangehenden Folgenglieder einbezieht
- Eine Linearkombination dieser Folgenglieder, in der beide Vorgänger den Koeffizienten +1 tragen
- Beide Startglieder gleich +1
Jedes dieser Kriterien erlaubt eine Verallgemeinerung:
- Die Wahl anderer Startglieder
und
liefert eine Folge
, die mit der kanonischen Folge nach der Beziehung
zusammenhängt. Ein Beispiel hierfür ist die Lucas-Folge
.
- Für die Glieder einer solchen Folge gilt ein gegenüber der Formel von
Moivre-Binet verallgemeinertes explizites Bildungsgesetz:
mit
und
.
- Die kanonische Folge stellt sich hier als Spezialfall mit
dar, was wegen der charakteristischen Gleichung sofort
und
liefert.
- Die Wahl anderer Koeffizienten für die Linearkombination liefert eine Folge, für die eine andere charakteristische Gleichung gilt. Eine Folge mit der Iterationsvorschrift
-
- besitzt die charakteristische Gleichung
. Die Wurzeln dieser Gleichung bestimmen das explizite Bildungsgesetz. Wenn die charakteristische Gleichung die Wurzeln
und
hat, dann lautet das Bildungsgesetz
- wobei
und
wieder durch die Startglieder bestimmt sind.
- Eine Iteration, die mehr als zwei vorangehende Folgenglieder
einbezieht, besitzt dementsprechend ein Polynom höheren Grades als
charakteristische Gleichung, wobei die Wurzeln
dieser Gleichung wieder im Bildungsgesetz auftauchen und die Koeffizienten
durch die Anfangswerte bestimmt sind. Es gilt dann
-
.
- Beispiele für derartige Folgen sind die Tribonacci- und die Tetranacci-Folge.
Die Perrin-Folge und die Padovan-Folge folgen
der Regel
.
- Eine Iteration, die nur das unmittelbar vorhergehende Glied verwendet, liefert in diesem Zusammenhang als entartete Fibonacci-Folge eine reine Potenzfolge.
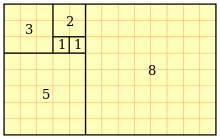
Fibonacci-Folgen in der Natur
Phyllotaxis

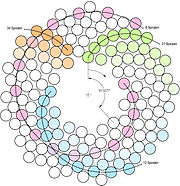
Die Blätter (Phyllotaxis) oder Fruchtstände vieler Pflanzen sind in Spiralen angeordnet, wobei die Anzahl dieser Spiralen den Fibonacci-Zahlen entsprechen. In diesem Fall ist der Winkel zwischen architektonisch benachbarten Blättern oder Früchten bezüglich der Pflanzenachse der Goldene Winkel. Das liegt daran, dass Brüche von aufeinanderfolgenden Fibonacci-Zahlen den zugrunde liegenden Goldenen Schnitt am besten approximieren. Die Spiralen werden daher von Pflanzenelementen gebildet, deren Platznummern sich durch die Fibonacci-Zahl im Nenner unterscheiden und damit fast in die gleiche Richtung weisen. Durch diese spiralförmige Anordnung der Blätter um die Sprossachse erzielt die Pflanze die beste Lichtausbeute. Der Versatz der Blätter um das irrationale Verhältnis des Goldenen Winkels sorgt dafür, dass nie Perioden auftauchen, wie es z.B. bei 1/4 der Fall wäre (0° 90° 180° 270° | 0° 90° …). Dadurch wird der denkbar ungünstigste Fall vermieden, dass ein Blatt genau senkrecht über dem anderen steht und so die Blätter maximalen Schatten auf darunterliegenden Blättern erzeugen oder maximale ‚Lichtlücken‘ entstehen.
Beispielsweise tragen die Körbe der Silberdistel (Carlina acaulis) hunderte gleichgestaltiger Blüten, die in kleineren Körben in einer 21-zu-55-Stellung, in größeren Körben in 34-zu-89- und 55-zu-144-Stellung in den Korbboden eingefügt sind. Auch die Schuppen von Fichtenzapfen wie auch von Ananasfrüchten bilden im und gegen den Uhrzeigersinn Spiralen, deren Schuppenanzahl durch zwei aufeinanderfolgende Fibonaccizahlen gegeben ist.
Wissenschaftshistorisch sei hier auf das Buch On Growth and Form von D’Arcy Wentworth Thompson (1917) verwiesen.
Stammbäume
Männchen der Honigbiene (Apis
mellifera) werden als Drohnen bezeichnet. Interessanterweise beschreibt die
Fibonacci-Folge die Anzahl der Ahnen einer Drohne. Das erklärt sich dadurch,
dass eine Drohne (Generation n = 1) sich aus einem unbefruchteten Ei
entwickelt, das ausschließlich Erbgut ihrer Mutter, der Bienenkönigin
(Generation n = 2), enthält; eine Drohne hat keinen Vater. Eine
Königin jedoch hat zwei Eltern, nämlich als Mutter eine andere Königin und als
Vater eine Drohne (Generation n = 3) usw. Die Anzahl aller Ahnen
einer Drohne in je einer so definierten n-ten Generation ist die
n-te Fibonacci-Zahl .
Um das einzusehen, lässt sich die Zeichnung zur Anzahl der Kaninchen in
Fibonaccis Modell im Abschnitt "Antike
und Mittelalter in Europa" verwenden. Jedes Paar nicht geschlechtsreifer
Kaninchen entspricht einer Drohne, jedes Paar geschlechtsreifer Kaninchen einer
Königin. In den Gleichungen der Modellierung ist dann
die Anzahl der Drohnen,
die Anzahl der Königinnen (jeweils in der n-ten Generation) und
die Anzahl der Ahnen einer Drohne in der betrachteten Generation.
Fettsäuren
Unverzweigte aliphatischen Monocarbonsäuren (hier: uaM), zu denen im Regelfall die Fettsäuren gehören, können verschieden viele Doppelbindungen an verschiedenen Positionen aufweisen. Die Anzahl der uaM gehorcht als Funktion der Kettenlänge der Fibonacci-Folge. Das folgt daraus, dass Doppelbindungen bei uaM nicht benachbart sind; die seltenen Ausnahmen sind hier vernachlässigt. Speziell gibt es nur eine aliphatische Monocarbonsäure mit einem C-Atom: Ameisensäure, eine mit zwei C-Atomen: Essigsäure, zwei mit dreien: Propionsäure und Acrylsäure usw. Bei 18 C-Atomen ergeben sich 2.584 Varianten (wovon Stearinsäure, Ölsäure, Linolsäure und Linolensäure vier Beispiele sind).
Auch hier lässt sich, um das einzusehen, die Zeichnung zur Anzahl der
Kaninchen in Fibonaccis Modell im Abschnitt "Antike
und Mittelalter in Europa" verwenden. Ein Kaninchenpaar der -ten
Generation entspricht dem
-ten
Kohlenstoffatom einer uaM, wobei die Zählung bei der Carboxygruppe beginnt.
Jedes Paar nicht geschlechtsreifer Kaninchen entspricht einem Kohlenstoffatom
,
auf das keine Doppelbindung folgen kann, jedes Paar geschlechtsreifer
Kaninchen einem Kohlenstoffatom
,
auf das eine Doppelbindung folgen kann (oder nicht). Die
Verbindungsstrecken von
nach
oder von
nach
entsprechen Einfachbindungen, die Verbindungsstrecken von
nach
Doppelbindungen. In den Gleichungen der Modellierung ist dann
(bzw.
)
die Anzahl der Kohlenstoffatome
(bzw.
).
– Jeder Pfad von
zu einem Kohlenstoffatom der
-ten
Generation entspricht genau einer uaM mit
Kohlenstoffatomen; die Zuordnung ist bijektiv.
Also ist die Anzahl
der in der
-ten
Generation betrachteten Kohlenstoffatome gleich der Anzahl der uaM mit
Kohlenstoffatomen.
Geschichte

Altes Indien
Ihre früheste Erwähnung findet sich unter dem Namen mātrāmeru („Berg der Kadenz“) in der Chhandah-shāstra („Kunst der Prosodie“) des Sanskrit-Grammatikers Pingala (um 450 v.Chr. oder nach anderer Datierung um 200 v.Chr.). In ausführlicherer Form behandelten später auch Virahanka (6. Jh.) und besonders dann Acharya Hemachandra (1089–1172) diese Zahlenfolge, um die rechnerische Möglichkeit der Bildung von Metren durch regelmäßige Verteilung kurzer und langer Silben zu beschreiben.
Antike und Mittelalter in Europa
In der westlichen Welt war diese Folge ebenfalls schon in der Antike Nikomachos von Gerasa (um 100 n.Chr.) bekannt. Sie ist aber mit dem Namen des italienischen Mathematikers Leonardo da Pisa, genannt Fibonacci („figlio di Bonacci“, Sohn des Bonacci), verbunden, der in seinem Liber abbaci („Buch der Rechenkunst“, Erstfassung von 1202 nicht erhalten, zweite Fassung von ca. 1227) diese Zahlenfolge mit dem Beispiel eines Kaninchenzüchters beschrieb, der herausfinden will, wie viele Kaninchenpaare innerhalb eines Jahres aus einem einzigen Paar entstehen, wenn jedes Paar ab dem zweiten Lebensmonat ein weiteres Paar pro Monat zur Welt bringt:
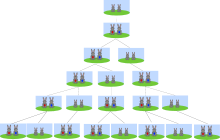

Fibonacci illustrierte diese Folge durch die einfache mathematische Modellierung des Wachstums einer Population von Kaninchen nach folgenden Regeln:[3]
- Jedes Paar Kaninchen wirft pro Monat ein weiteres Paar Kaninchen.
- Ein neugeborenes Paar bekommt erst im zweiten Lebensmonat Nachwuchs (die Austragungszeit reicht von einem Monat in den nächsten).
- Die Tiere befinden sich in einem abgeschlossenen Raum („in quodam loco, qui erat undique pariete circumdatus“), sodass kein Tier die Population verlassen und keines von außen hinzukommen kann.
Fibonacci begann die Folge, nicht ganz konsequent, nicht mit einem neugeborenen, sondern mit einem trächtigen Paar, das seinen Nachwuchs bereits im ersten Monat wirft, sodass im ersten Monat bereits 2 Paare zu zählen sind. In jedem Folgemonat kommt dann zu der Anzahl der Paare, die im Vormonat gelebt haben, eine Anzahl von neugeborenen Paaren hinzu, die gleich der Anzahl derjenigen Paare ist, die bereits im vorvergangenen Monat gelebt hatten, da der Nachwuchs des Vormonats noch zu jung ist, um jetzt schon seinerseits Nachwuchs zu werfen. Fibonacci führte den Sachverhalt für die zwölf Monate eines Jahres vor (2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377) und wies auf das Bildungsgesetz der Folge durch Summierung jeweils zweier aufeinanderfolgender Folgenglieder (2+3 = 5, 3+5 = 8, 5+8 = 13 usw.) hin. Er merkte außerdem an, dass die Folge sich nach diesem Prinzip für eine unendliche Zahl von Monaten fortsetzen lässt, was dann allerdings unsterbliche Kaninchen voraussetzt: „et sic posses facere per ordinem de infinitis numeris mensibus.“ Weitere Beachtung hatte er dem Prinzip in seinen erhaltenen Werken nicht geschenkt.
Eine 2014 erschienene, mathematisch-historische Analyse zum Leben des Leonardo von Pisa, insbesondere zu seinem Aufenthalt in der nordafrikanischen Hafenstadt Bejaia (im heutigen Algerien), kam zu dem Schluss, dass der Hintergrund der Fibonacci-Folge gar nicht bei einem Modell der Vermehrung von Kaninchen zu suchen ist (was schon länger vermutet wurde), sondern vielmehr bei den Bienenzüchtern von Bejaia und ihrer Kenntnis des Bienenstammbaums zu finden ist. Zu Leonardos Zeit war Bejaia ein wichtiger Exporteur von Bienenwachs, worauf noch heute der französische Name der Stadt (Bougie, wie das frz. Wort für Kerze) hinweist.
Nachdem spätere Mathematiker wie Gabriel Lamé (1795–1870) die Entdeckung dieser Zahlenfolge für sich beansprucht hatten, brachten Édouard Lucas (1842–1891) und andere wieder in Erinnerung, dass der zu dieser Zeit älteste bekannte Beleg von Leonardo da Pisa stammte, und unter dem Namen „Fibonacci-Folge“ („suite de Fibonacci“, „Fibonacci sequence“, „successione di Fibonacci“) ist sie seither in den meisten westlichen Sprachen geläufig.
-
Mathematische Modellierung des Wachstums von Fibonaccis Kaninchen-Population Sei
die Anzahl der geschlechtsreifen bzw.
die Anzahl der nicht geschlechtsreifen Kaninchen der
-ten Generation, entsprechend für die Generationen
und
. Nach den oben angegebenen Regeln ist mit diesen Bezeichnungen:
(1);
(1');
(2);
Einsetzen von (1') in (1) und anschließende Addition von (2) ergibt:
,
für die Gesamtzahl
,
,
von Kaninchen der jeweiligen Generation also
, was dem angegebenen rekursiven Bildungsgesetz der Fibonacci-Folge äquivalent ist.
Mit
beschreibt dieses Modell die in der Zeichnung angegebenene Generationenfolge.
Fibonacci-Datenstrukturen
Die Fibonacci-Folge ist namensgebend für folgende Datenstrukturen, bei deren mathematischer Analyse sie auftritt.
- Fibonacci-Baum
- Fibonacci-Heap
Verwandte der Fibonacci-Folge
Die Prinzipien der Fibonacci-Folge können auch auf ähnliche Zahlenfolgen angewendet. So besteht die Tribonacci-folge, gleichfalls aus aufeinanderaddierten Zahlen. Hierbei werden aber jeweils die ersten drei Zahlen zusammengezählt um die jeweils nächste zu bilden.
für
Die ersten Glieder lauten:
- 0, 1, 1, 2, 4, 7, …
Die Tribonaccizahlen tauchen bei einigen geometrischen Figuren auf.
Genau wie die Fibonaccizahlen aus 2 und die Tribonaccizahlen aus 3 Gliedern errechenbar sind lassen sich die n-Bonaccizahlen (So auch Tetra- und Pentanaccizahlen) aus n Gliedern bilden.
Literatur
- Huberta Lausch: Fibonacci und die Folge(n). Oldenbourg 2010, ISBN 978-3-486-58910-8.
Anmerkungen
- ↑ Obwohl viele der Aussagen weiter unten auch gelten, wenn die Indizes (Subskripte) um einen festen Betrag verschoben werden, hat sich diese Festlegung eingebürgert. Sie hat auch den Vorteil, dass die Ergänzung auf negative Indizes sich symmetrisch zur 0 verhält.
- ↑ In manchen Büchern wird für de Moivres Entdeckung auch 1730 angegeben oder auch die Entdeckung nur Binet zugeschrieben.
- ↑ Dazu muss festgestellt werden, dass dies ein theoretisches Gedankenmodell ist, welches sich in der Praxis nicht so abbildet. Der Grund liegt in den individuellen Genen der Kaninchenmütter und der sich verändernden Geburtenrate. Es gibt Mütter, die über die Zeit zunehmend mehr Nachkommen haben, wenn sie mehr gebären konnten, während andere weniger Nachkommen haben, nachdem sie einen großen Wurf hatten. Zudem passen Kaninchen wie auch Mäuse ihre Wurfgröße genetisch festgelegt an das Nahrungsangebot an, indem sie Gene an und abschalten, welche die Fertilität steuern und Keimverzögerung sowie Befruchtungswillen beeinflussen.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 23.07. 2024