Abrundungsfunktion und Aufrundungsfunktion
Die Abrundungsfunktion (auch Gaußklammer,
Ganzzahl-Funktion, Ganzteilfunktion oder Entier-Klammer)
und die Aufrundungsfunktion sind Funktionen, die einer reellen Zahl die
nächstliegende nicht größere bzw. nicht kleinere ganze
Zahl zuordnen. Die Notation wurde nach Carl
Friedrich Gauß benannt, der das Symbol
für die Abrundungsfunktion 1808 einführte.
Ende des 20. Jahrhunderts verbreiteten sich auch die von Kenneth E. Iverson
eingeführten Bezeichnungen
und
(engl. floor „Boden“) für die Gaußklammer sowie
und
(engl. ceiling „Decke“) für die Aufrundungsfunktion.
Im Deutschen bezieht sich das Wort Gaußklammer ohne weitere Zusätze meist auf
die ursprüngliche von Gauß verwendete Notation.
Für die von Iverson eingeführten Varianten werden dann zur Unterscheidung die
Bezeichnungen untere Gaußklammer und obere Gaußklammer
verwendet.
Abrundungsfunktion oder Gaußklammer
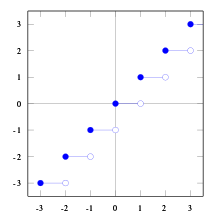
Definition
Sie ist folgendermaßen definiert:
- Für eine reelle
Zahl
ist
die größte ganze Zahl, die kleiner oder gleich
ist:
Beispiele
-
- Man beachte, dass
nicht etwa gleich
ist. Die Definition verlangt ja
, und es ist
.
- Man beachte, dass
Eigenschaften
- Für alle
gilt
.
- Es gilt immer
. Dabei ist
genau dann, wenn
eine ganze Zahl ist.
- Für jede ganze Zahl
und jede reelle Zahl
gilt
.
- Für alle reellen Zahlen
gilt
.
- Für jede ganze Zahl
und jede natürliche Zahl
gilt
.
- Die Abrundungsfunktion ist idempotent:
Es gilt
.
- Sind
und
teilerfremde natürliche Zahlen, dann gilt
.
- Die Abrundungsfunktion ist nicht stetig, aber oberhalbstetig.
- Für nichtganze reelle
konvergiert die Fourierreihe der
-periodischen Funktion
, und es gilt
.
- Sind
und
, so gilt
.
- Daraus folgt direkt, dass, falls
,
.
- Ferner gilt auch
.
Aufrundungsfunktion
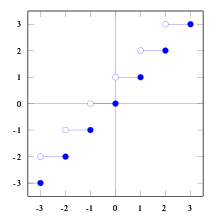
Definition
Sie ist so definiert:
- Für eine reelle Zahl
ist
die kleinste ganze Zahl, die größer oder gleich
ist.
Beispiele
Eigenschaften
- Es gilt analog
- Sind
und
, so gilt
.
- Daraus folgt direkt, dass, falls
,
.
Allgemeine Eigenschaften
Gaußklammer und Dezimalstellen
Es gilt für positive Zahlen:
- Die Funktion
liefert dabei den Nachkommaanteil mit
.
Zusammenhänge zwischen Auf- und Abrundungsfunktion
- Es ist stets
- Deshalb erhält man die Aufrundungsfunktion aus der Gaußklammerfunktion per
- Kippregeln von Brüning
- Für ganze Zahlen
gilt:
Kaufmännische Rundung
Die kaufmännische Rundung auf die nächstliegende ganze Zahl kann auch mit diesen Funktionen ausgedrückt werden:
Dasselbe Ergebnis liefert, wenn auch mit einer etwas komplizierteren Formel, dafür unabhängig vom Vorzeichen des Arguments, die Funktion
.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 23.07. 2019