Gammafunktion

Graph der Gammafunktion im Reellen

Komplexe Gammafunktion: Die Helligkeit entspricht dem Betrag, die Farbe dem Argument des Funktionswerts. Zusätzlich sind Höhenlinien konstanten Betrags eingezeichnet.

Betrag der komplexen Gammafunktion

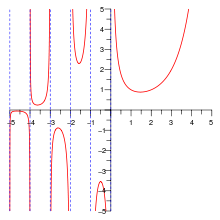
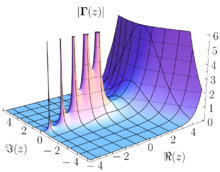
Die Eulersche Gammafunktion, auch kurz Gammafunktion oder Eulersches Integral zweiter Gattung, ist eine der wichtigsten speziellen Funktionen und wird in den mathematischen Teilgebieten der Analysis und der Funktionentheorie untersucht. Sie wird heute durch ein $\Gamma$ , den griechischen Großbuchstaben Gamma, bezeichnet und ist eine transzendente meromorphe Funktion mit der Eigenschaft

$\Gamma (n)=(n-1)!$

für jede natürliche Zahl , wobei mit die Fakultät bezeichnet wird. Die Motivation zur Definition der Gammafunktion war, die Fakultätsfunktion auf reelle und komplexe Argumente erweitern zu können. Der Schweizer Mathematiker Leonhard Euler löste im Jahr 1729 diese Fragestellung und definierte die Gammafunktion mittels eines unendlichen Produktes. Heute wird die Gammafunktion oft mittels einer Integraldarstellung definiert, die ebenfalls auf Euler zurückgeht.

Die Gammafunktion liegt der Gamma-Wahrscheinlichkeitsverteilung zugrunde.

Einordnung ohne mathematisches Vorwissen

Eine mathematische Funktion ist im Grunde wie eine Rechenmaschine. Man gibt einen Wert in die Funktion ein, und diese liefert dann ein Ergebnis in Abhängigkeit vom Eingabewert, zumindest theoretisch. Damit ist gemeint, dass die Funktion an sich nicht rechnet, sondern meist nur eine Rechenvorschrift formelhaft festhält. Einfaches Beispiel für eine Funktion ist die quadratische Funktion, welche die Eingabe mit sich selbst multipliziert. Formelhaft schreibt man dies als $f(x)=x^{2}$ . Somit ordnet die quadratische Funktion beispielsweise der Zahl den Wert $(-2)^{2}$ zu. Rechnet man dies aus, ergibt sich $4$ , also $f(-2)=4$ .

Die Gammafunktion fußt auf einer Vorschrift, die auch als Fakultät bekannt ist. Diese ordnet einer natürlichen Zahl das Produkt aller natürlichen Zahlen bis zu dieser Zahl zu. Bezeichnet wird die Fakultät mit dem Symbol des Ausrufezeichens. Also gilt zum Beispiel

$4!=1\cdot 2\cdot 3\cdot 4=24.$

Es galt innerhalb der Mathematik als Problem, ob sich diese Vorschrift auch auf Zahlen anderer Art erweitern ließe. Konkret bedeutet das:

Lassen sich Fakultäten auch für beliebige rationale, reelle, komplexe Zahlen berechnen? Wie in etwa könnte man sich $({\tfrac {1}{2}})!$ vorstellen?
Falls solche „universelle“ Vorschriften gefunden werden, welche mathematischen Eigenschaften können ihnen gegeben werden? Zeichnet sich eine dieser Vorschriften als ganz besonders natürlich und strukturell aus? Ist diese besondere Vorschrift eindeutig bestimmt, also „die eine“ verallgemeinerte Fakultät?

Die Antwort auf diese Fragen liefert die Gammafunktion. Für beliebige Werte liefert $\Gamma (z+1)=z!$ , also gilt zum Beispiel $\Gamma (5)=24.$ Die Verschiebung um 1 von der oben erwähnten Fakultät ist auf eine Konvention aus dem 19. Jahrhundert zurückzuführen. Die Strategie der Verallgemeinerung basiert auf der Beobachtung, dass aus einer vorherigen Fakultät durch Hinzunahme eines weiteren Faktors eine weitere Fakultät gewonnen wird. In etwa gilt $4!\cdot 5=5!$ und ganz allgemein $n!\cdot (n+1)=(n+1)!$ . Demnach sollten sämtliche Werte der Gammafunktion mittels $\Gamma (z)\cdot z=\Gamma (z+1)$ in Relation stehen. Stellt man weitere wichtige Bedingungen, wie Differenzierbarkeit, an $\Gamma (z)$ , so kann diese schließlich eindeutig definiert werden, womit „die“ verallgemeinerte Fakultät gefunden ist.

Es gilt dann $({\tfrac {1}{2}})!=\Gamma ({\tfrac {3}{2}})={\tfrac {\sqrt {\pi }}{2}}\approx 0{,}88622$ mit der Kreiszahl $\pi$ . Dieser Zusammenhang lässt sich über die Normalverteilung von Gauß erklären.

Geschichte

Als früheste Definition der Gammafunktion gilt die in einem Brief von Daniel Bernoulli an Christian Goldbach vom 6. Oktober 1729 gegebene:

$\Bigl(A + \frac{x}{2}\Bigr)^{x-1} \Bigl(\frac{2}{1+x} \cdot \frac{3}{2+x} \cdot \frac{4}{3+x} \cdots \frac{A}{A-1+x}\Bigr)$

für unendlich große , entsprechend heutiger Notation oder $\Gamma(x+1)$ . Wenige Tage später, am 13. Oktober^jul./ 24. Oktober 1729^greg., beschrieb Euler ebenfalls in einem Brief an Goldbach die ähnliche, etwas einfachere Formel

${\frac {1\cdot 2\cdot 3\dotsm n}{(1+m)(2+m)\dotsm (n+m)}}\,(n+1)^{m},$

die Gauß 1812 für den allgemeineren Fall komplexer Zahlen wiederentdeckte (die genannten Briefe wurden erst 1843 herausgegeben). Sie nähert sich mit wachsendem dem wahren Wert für oder $\Gamma(m+1)$ . Am 8. Januar 1730 beschrieb Euler in einem Brief an Goldbach folgendes Integral zur Interpolation der Fakultätsfunktion, das er am 28. November 1729 der St. Petersburger Akademie vorgestellt hatte:

$\int \!{\mathrm d}x(-lx)^{n},$ in heutiger Notation: $\displaystyle \Gamma (n+1)=\int _{0}^{1}(-\log x)^{n}\mathrm {d} x$

Diese Definition wurde von Euler später bevorzugt verwendet und geht durch die Substitution $t = -\log x$ in die Form

$\Gamma (n+1)=\int _{0}^{\infty }t^{n}{\mathrm {e}}^{{-t}}{\mathrm d}t$

über. Euler entdeckte dieses Integral bei der Untersuchung eines Problems aus der Mechanik, bei dem die Beschleunigung eines Teilchens betrachtet wird.

Adrien-Marie Legendre führte 1809 die griechische Majuskel $\Gamma$ (Gamma) als Funktionssymbol ein. Gauß verwendete 1812 das Funktionssymbol $\Pi$ (Pi) so, dass $\Pi(x) = \Gamma(x+1)$ und somit auch $\Pi(n) = n!$ für nichtnegative ganzzahlige gilt. Es setzte sich jedoch nicht durch; heute wird $\Pi$ als Symbol für ein Produkt benutzt (analog zu $\Sigma$ für eine Summe).

Definition und elementare Darstellungsformen

Es gibt in der Literatur keine einheitliche Definition für die Gammafunktion.

Häufig wird das Eulersche Integral zweiter Gattung gegeben. Ein Nachteil ist, dass dieses Integral nicht überall konvergiert. Somit ist eine globale Berechnung mittels dieser Definition nur indirekt möglich. Für komplexe Zahlen mit positivem Realteil ist die Gammafunktion damit das uneigentliche Integral

$\Gamma (z)=\int _{0}^{\infty }t^{z-1}{\mathrm {e} }^{-t}\mathrm {d} t.$

Die dadurch definierte Funktion ist holomorph, da das Integral (wegen des schnellen Abfallens der Exponentialfunktion) auf kompakten Mengen gleichmäßig konvergiert. Dies ermöglicht den Einsatz des Weierstraßschen Konvergenzsatzes. Mittels meromorpher Fortsetzung lässt sich $\Gamma (z)$ schließlich für alle Werte $\mathbb {C} \setminus \{0,-1,-2,\dotsc \}$ berechnen.

Eine andere Darstellung mittels eines Produktes motiviert die Verallgemeinerung der Fakultät auf direkte Weise. Sie ist gegeben durch:

$\Gamma (z)=\lim _{n\to \infty }{\frac {n!\,n^{z}}{z(z+1)(z+2)\dotsm (z+n)}}.$

In seinem Buch Number Theory. Analytic and modern tools. gibt Henri Cohen eine Definition mittels der Hurwitzschen Zeta-Funktion. Als Begründung hierfür wird eine „einfache Möglichkeit der Verallgemeinerung“ und die „Betonung wichtiger Formeln“ angegeben. Es gilt demnach für komplexe Zahlen mit positivem Realteil

$\Gamma (z)=\exp(\zeta '(0,z)-\zeta '(0,1)),$

wobei die Ableitung bezüglich der ersten Variablen gebildet ist.

Globale Eigenschaften

Funktionalgleichung und Meromorphie

Die Gammafunktion erfüllt in ihrem Definitionsbereich für alle die Funktionalgleichung

$z\Gamma (z)=\Gamma (z+1).$

Mittels dieser Relation ist eine induktive Fortsetzung (beispielsweise des Eulerschen Integrals) möglich. Es gilt für alle $n=0,1,2,\dotsc$ :

$\Gamma (z)={\frac {\Gamma (z+n+1)}{z(z+1)(z+2)\cdots (z+n)}}.$

Es kann gefolgert werden, dass $\Gamma (z)$ eine in ganz $\mathbb {C} \setminus \{0,-1,-2,\dotsc \}$ holomorphe Funktion ist und einfache Pole in allen Punkten $z=0,-1,-2,\dotsc$ besitzt. Für das dortige Residuum gilt

$\operatorname {res} _{z=-n}\Gamma (z)={\frac {(-1)^{n}}{n!}}.$

Der Satz von Hölder

Der Satz von Hölder (Otto Hölder 1886) ist ein Negativresultat und besagt, dass die Gammafunktion keine algebraische Differentialgleichung erfüllt, deren Koeffizienten rationale Funktionen sind. Das heißt, es gibt keine Differentialgleichung der Form $f(z,y(z),y'(z),\dotsc ,y^{(n)}(z))=0$ mit einer nichtnegativen ganzen Zahl und einem Polynom $f \neq 0$ in $y,y',\dotsc ,y^{(n)}$ , dessen Koeffizienten rationale Funktionen von sind, und der Lösung $y = \Gamma$ .

Axiomatische Charakterisierung

Fortsetzung der Fakultät

Die Bedingungen G(1) = 1 und $G(x+1) = x \cdot G(x)$ , die die Fakultät für natürliche Zahlen eindeutig beschreiben, werden auch von anderen analytischen Funktionen als der Gammafunktion erfüllt. Für positive erfüllt beispielsweise die Funktion

$G(x) = \Gamma(x) \cdot \bigl(1 + c\,\sin(2\pi x)\bigr)$

für 0<c<1 die charakteristischen Bedingungen der Gammafunktion. Weierstraß fügte 1854 daher die notwendige und hinreichende Bedingung

$\lim_{n \to \infty} \frac{G(x+n)}{G(n)\,n^x} = 1$

hinzu, womit aber die Suche nach einer möglichst elementaren oder natürlichen charakterisierenden Eigenschaft nicht beendet war. Emil Artin diskutierte 1931 die mögliche Kennzeichnung durch Funktionalgleichungen.

Der Satz von Bohr-Mollerup

Der Satz von Bohr-Mollerup (Harald Bohr und Johannes Mollerup 1922) erlaubt eine einfache Charakterisierung der Gammafunktion:

Eine Funktion $G\colon\mathbb R_{>0}\to\mathbb R_{>0}$ ist in diesem Bereich genau dann gleich der Gammafunktion, wenn gilt:

$G(x+1) = x \cdot G(x),$
ist logarithmisch konvex, das heißt, $x\mapsto\log G(x)$ ist eine konvexe Funktion.

Diese Axiome sind bei Nicolas Bourbaki der Ausgangspunkt für die Darstellung der Theorie der Gammafunktion.

Der Satz von Wielandt

Der Satz von Wielandt über die Gammafunktion (Helmut Wielandt 1939) charakterisiert die Gammafunktion als holomorphe Funktion und besagt:

Eine holomorphe Funktion , definiert auf einem Gebiet , das den Streifen $S=\{x\mid 1\leq \operatorname {Re} (x)<2\}$ enthält, ist genau dann gleich der Gammafunktion auf , wenn gilt:

$G(x+1) = x \cdot G(x),$
ist auf dem Streifen beschränkt, das heißt, es existiert ein , sodass für alle aus .

Genauer gilt $|\Gamma (x)|\leq \Gamma (\operatorname {Re} (x))$ für alle mit $\operatorname {Re} (x)>0$ .

Weitere Darstellungsformen

Neben der Darstellung der Gammafunktion aus der Definition gibt es noch andere äquivalente Darstellungen. Eine direkte Definition von $\Gamma (x)$ für alle $x\in \mathbb {C} \setminus \{0,-1,-2,\dotsc \}$ gibt die Produktdarstellung der Gammafunktion nach Gauß,

$\Gamma (x)=\lim _{n\to \infty }{\frac {n!\,n^{x}}{x(x+1)(x+2)\dotsm (x+n)}},$

die für positive reelle Zahlen bereits von Euler 1729 angegeben wurde. Daraus abgeleitet ist die Darstellung von $1 / \Gamma$ als Weierstraß-Produkt:

$1 / \Gamma(x) = x \cdot \prod_{n=1}^\infty \left(1+\frac{x}{n}\right) \mathrm{e}^{-x \log(\frac{n+1}{n})} = x \cdot \mathrm{e}^{\gamma\,x} \cdot \prod_{n=1}^\infty \left(1+\frac{x}{n}\right) \mathrm{e}^{-x/n}$

mit der Eulerschen Konstante $\gamma = \lim_{n \to \infty} \bigl((\tfrac{1}{1} + \tfrac {1}{2} + \tfrac {1}{3} + \dotsb + \tfrac{1}{n}) - \log n\bigr)$ . Das zweite Produkt wird üblicherweise als Weierstraßsche Darstellung bezeichnet, Karl Weierstraß verwendete jedoch nur das erste.

Die Integraldarstellung aus der Definition geht ebenfalls auf Euler 1729 zurück, sie gilt allgemeiner für komplexe Zahlen mit positivem Realteil:

$\Gamma (x)=\int _{0}^{\infty }t^{{x-1}}{\mathrm {e}}^{{-t}}\,{\mathrm d}t,$ wenn $\operatorname {Re} (x)>0$

Durch die Zerlegung dieses Integrals folgerte E. F. Prym 1876 eine in ganz $\mathbb {C} \setminus \{0,-1,-2,-3,\dotsc \}$ gültige Darstellung:

$\Gamma (x)=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{n!(n+x)}}+\int _{1}^{\infty }t^{x-1}e^{-t}\mathrm {d} t$

Eine andere Variante der Eulerschen Integraldarstellung gibt es für $x \in \mathbb{C}$ mit $0 < \operatorname{Re}(x) < 1$ :

$\Gamma (x)=\mathrm {e} ^{\pi \mathrm {i} x/2}\int _{0}^{\infty }t^{x-1}\mathrm {e} ^{-\mathrm {i} t}\,\mathrm {d} t$

Aus dieser Darstellung lassen sich zum Beispiel auf elegante Weise die Fresnelschen Integralformeln ableiten.

Ernst Eduard Kummer gab 1847 die Fourierentwicklung der logarithmischen Gammafunktion an:

$\log\Gamma(x) = \left(\tfrac{1}{2}-x\right) \bigl(\gamma + \log(2\pi)\bigr) + \frac{1}{2} \log\frac{\pi}{\sin(\pi x)} + \frac{1}{\pi} \sum_{k=2}^\infty \frac{\log k}{k} \sin(2\pi k x)$ für 0<x<1

Sie heißt auch Kummersche Reihe. Bereits 1846 fand Carl Johan Malmstén eine ähnliche Reihe:

$\log {\frac {\Gamma ({\tfrac {1}{2}}+x)}{\Gamma ({\tfrac {1}{2}}-x)}}=-2x\,{\bigl (}\gamma +\log(2\pi ){\bigr )}+{\frac {2}{\pi }}\sum _{k=2}^{\infty }(-1)^{k}{\frac {\log k}{k}}\sin(2\pi kx)$ für $-{\tfrac {1}{2}}<x<{\tfrac {1}{2}}$

Funktionalgleichungen und spezielle Werte

Die Gammafunktion genügt der Funktionalgleichung

$\Gamma(x+1) = x \cdot \Gamma(x)$ mit $\Gamma(1) = 1.$

Im Folgenden wird $\Gamma ({\tfrac {1}{2}})$ ermittelt:

$\Gamma ({\tfrac {1}{2}})=\int _{0}^{\infty }x^{-1/2}\exp(-x)\,\mathrm {d} x=2\int _{0}^{\infty }\exp(-x^{2})\,\mathrm {d} x$

$[\int _{0}^{\infty }\exp(-x^{2})\,\mathrm {d} x]^{2}=\int _{0}^{\infty }2\exp(-x^{2})[\int _{0}^{1}x\exp(-x^{2}y^{2})\,\mathrm {d} y]\,\mathrm {d} x=\int _{0}^{\infty }\int _{0}^{1}2x\exp(-x^{2})\exp(-x^{2}y^{2})\,\mathrm {d} y\,\mathrm {d} x=$

$=\int _{0}^{1}\int _{0}^{\infty }2x\exp(-x^{2})\exp(-x^{2}y^{2})\,\mathrm {d} x\,\mathrm {d} y=\int _{0}^{1}\int _{0}^{\infty }2x\exp[-x^{2}(y^{2}+1)]\,\mathrm {d} x\,\mathrm {d} y=\int _{0}^{1}{\frac {1}{y^{2}+1}}\mathrm {d} y={\frac {\pi }{4}}$

Daraus folgt: $\Gamma ({\tfrac {1}{2}})={\sqrt {\pi }}$

Alternativ kann dieser Gammafunktionswert mit dem Wallisschen Produkt ermittelt werden:

$\prod _{k=1}^{\infty }{\frac {4k^{2}}{4k^{2}-1}}={\frac {\pi }{2}}$

Dieses Produkt lässt sich auf diese Weise umformen:

$\prod _{k=1}^{\infty }{\frac {4k(k+1)}{(2k+1)^{2}}}={\frac {\pi }{4}}$

Folgender Bruch hat folgenden Grenzwert:

$\lim _{n\rightarrow \infty }{\frac {\Gamma (n+1){\sqrt {n+1}}}{\Gamma (n+3/2)}}=1$

Für alle n ∈ ℕ gelten folgende Ausdrücke:

$\Gamma (n+1){\sqrt {n+1}}=\prod _{k=1}^{n}{\sqrt {k(k+1)}}$

${\frac {1}{\Gamma (n+3/2)}}={\frac {1}{\Gamma (3/2)}}\prod _{k=1}^{n}{\frac {2}{2k+1}}$

Folglich gilt diese Formel:

$\lim _{n\rightarrow \infty }\left[\prod _{k=1}^{n}{\sqrt {k(k+1)}}{\frac {1}{\Gamma (3/2)}}\prod _{k=1}^{n}{\frac {2}{2k+1}}\right]=1$

Die Formel wird nach Γ(3/2) aufgelöst:

$\Gamma (3/2)=\lim _{n\rightarrow \infty }\left[\prod _{k=1}^{n}{\sqrt {k(k+1)}}\prod _{k=1}^{n}{\frac {2}{2k+1}}\right]=$

$=\lim _{n\rightarrow \infty }\left[\prod _{k=1}^{n}{\sqrt {k(k+1)}}{\frac {2}{2k+1}}\right]=\prod _{k=1}^{\infty }{\sqrt {k(k+1)}}{\frac {2}{2k+1}}=$

$={\sqrt {\prod _{k=1}^{\infty }{\frac {4k(k+1)}{(2k+1)^{2}}}}}={\sqrt {\frac {\pi }{4}}}={\frac {1}{2}}{\sqrt {\pi }}$

Daraus folgt:

$\Gamma (1/2)=2\Gamma (3/2)={\sqrt {\pi }}$

Mit dem Ergänzungssatz der Gammafunktion (Euler 1749)

$\Gamma (x)\cdot \Gamma (1-x)={\frac {\pi }{\sin(\pi x)}}$ für $x \in \mathbb{C} \setminus \mathbb{Z}$

erhält man ebenso $\Gamma ({\tfrac {1}{2}})={\sqrt {\pi }}=1{,}77245\,38509\,05516\,02729\dotso$ (Folge A002161 in OEIS) sowie

$\Gamma(-n+\tfrac{1}{2}) = \frac{n!\,(-4)^n}{(2n)!}\,\sqrt{\pi}$ und $\Gamma(n+\tfrac{1}{2}) = \frac{(2n)!}{n!\,4^n}\,\sqrt{\pi}$ für $n=0,1,2,\dotsc$

Mit allgemeiner gewähltem wird aus der letzten Formel die Legendresche Verdopplungsformel (Legendre 1809)

$\Gamma\left(\frac{x}{2}\right) \cdot \Gamma\left(\frac{x+1}{2}\right) = \frac{\sqrt{\pi}}{2^{x-1}} \cdot \Gamma(x)$ für $x\in \mathbb {C} \setminus \{0,-1,-2,\dotsc \}.$

Diese ist ein Spezialfall der Gaußschen Multiplikationsformel (Gauß 1812)

$\Gamma\left(\frac{x}{n}\right) \cdot \Gamma\left(\frac{x+1}{n}\right) \cdots \Gamma\left(\frac{x+n-1}{n}\right) = \frac{(2\pi)^{(n-1)/2}}{n^{\,x-1/2}}\cdot\Gamma(x)$ für $n = 1,\,2,\,3,\,\ldots$ und $x\in \mathbb {C} \setminus \{0,-1,-2,\dotsc \}.$

Gregory Chudnovsky zeigte 1975, dass jede der Zahlen $\Gamma(1/6)$ , $\Gamma (1/4)$ , $\Gamma(1/3)$ , $\Gamma(2/3)$ , $\Gamma(3/4)$ und $\Gamma(5/6)$ transzendent und algebraisch unabhängig von $\pi$ ist. Hingegen ist beispielsweise von dem Funktionswert $\Gamma (1/5)=4{,}59084\,37119\,98803\,05320\,\dotso$ (Folge A175380 in OEIS) nicht einmal bekannt, ob er irrational ist.

Mit der lemniskatischen Konstante $\varpi$ gilt

$\Gamma \left({\frac {1}{4}}\right)=4\cdot \Gamma \left({\frac {5}{4}}\right)={\sqrt {2\varpi \,{\sqrt {2\pi }}}}=3{,}62560\,99082\,21908\,31193\dotso$ (Folge A068466 in OEIS).

Denn es gilt Folgendes:

$\Gamma \left({\frac {5}{4}}\right)^{2}=[\int _{0}^{\infty }\exp(-x^{4})\,\mathrm {d} x]^{2}=\int _{0}^{1}\int _{0}^{\infty }2x\exp(-x^{4})\exp(-x^{4}y^{4})\,\mathrm {d} x\,\mathrm {d} y=\int _{0}^{1}\int _{0}^{\infty }2x\exp[-x^{4}(y^{4}+1)]\,\mathrm {d} x\,\mathrm {d} y=$

$=\int _{0}^{1}\int _{0}^{\infty }\exp[-x^{2}(y^{4}+1)]\,\mathrm {d} x\,\mathrm {d} y=\int _{0}^{1}{\frac {1}{\sqrt {y^{4}+1}}}\mathrm {d} y\int _{0}^{\infty }\exp(-x^{2})\,\mathrm {d} x={\frac {\varpi }{2{\sqrt {2}}}}\int _{0}^{\infty }\exp(-x^{2})\,\mathrm {d} x={\frac {\varpi {\sqrt {\pi }}}{4{\sqrt {2}}}}$

Hierbei gilt folgende Formel über den Arcussinus lemniscatus: ${\frac {1}{\sqrt {y^{4}+1}}}={\frac {\mathrm {d} }{\mathrm {d} y}}{\sqrt {2}}\cdot \mathrm {arcsl} \left({\frac {y}{\sqrt {{\sqrt {y^{4}+1}}+1}}}\right)$

Die Gammafunktionswerte der Drittel können ebenso mit Hilfe elliptischer Integrale erster und zweiter Ordnung dargestellt werden:

$\Gamma \left({\frac {1}{3}}\right)=3\cdot \Gamma \left({\frac {4}{3}}\right)={\frac {2^{7/9}}{3^{1/12}}}{\pi }^{1/3}{K[\sin({\frac {\pi }{12}})]}^{1/3}$

$\Gamma \left({\frac {2}{3}}\right)={\frac {3}{2}}\cdot \Gamma \left({\frac {5}{3}}\right)={\frac {2^{2/9}}{3^{5/12}}}{\pi }^{2/3}{K[\sin({\frac {\pi }{12}})]}^{-1/3}={\frac {2^{5/9}}{3^{5/12}}}{\pi }^{1/3}[{2{\sqrt {3}}E[\sin({\frac {\pi }{12}})]-({\sqrt {3}}+1)K[\sin({\frac {\pi }{12}})]}]^{1/3}$

Denn es gilt Folgendes:

$\Gamma \left({\frac {4}{3}}\right)^{2}=[\int _{0}^{\infty }\exp(-x^{3})\,\mathrm {d} x]^{2}=\int _{0}^{1}\int _{0}^{\infty }2x\exp(-x^{3})\exp(-x^{3}y^{3})\,\mathrm {d} x\,\mathrm {d} y=$

$=\int _{0}^{1}\int _{0}^{\infty }2x\exp[-x^{3}(y^{3}+1)]\,\mathrm {d} x\,\mathrm {d} y=\int _{0}^{1}{\frac {1}{(y^{3}+1)^{2/3}}}\mathrm {d} y\int _{0}^{\infty }2x\exp(-x^{3})\,\mathrm {d} x={\frac {2^{1/3}}{3^{3/4}}}K[\sin({\frac {\pi }{12}})]\Gamma \left({\frac {5}{3}}\right)$

Wegen der Eulerschen Formel des Ergänzungssatzes gilt: $\Gamma \left({\frac {4}{3}}\right)\Gamma \left({\frac {5}{3}}\right)={\frac {4\pi }{9{\sqrt {3}}}}$

Die Steigung der Gammafunktion an der Stelle 1 ist gleich dem Negativen der Euler-Mascheroni-Konstante $\gamma$ :

$\Gamma'(1) = -\gamma$

Die Gammafunktion hat an den Stellen $x=-n\ \left(n=0,1,2,\dotsc \right)$ Pole erster Ordnung. Aus der Funktionalgleichung erhält man für die Residuen

$\operatorname {Res} _{x=-n}\Gamma (x)={\frac {(-1)^{n}}{n!}}.$

Alternativ lassen sie sich direkt an der Formel

$\Gamma (z)=\sum _{{n=0}}^{\infty }{\frac {(-1)^{n}}{n!}}{\frac {1}{z+n}}+\int _{1}^{\infty }t^{{z-1}}e^{{-t}}{\mathrm d}t$

ablesen. Da $\Gamma$ keine Nullstellen hat, ist $1 / \Gamma$ eine ganze Funktion.

Zusammenhang mit der Riemannschen ζ-Funktion

Bernhard Riemann brachte 1859 die Gammafunktion mit der Riemannschen ζ-Funktion über die Formel

$\Gamma (s)\,\zeta (s)=\int _{0}^{\infty }{\frac {x^{{s-1}}}{{\mathrm {e}}^{x}-1}}\,{\mathrm d}x$

und die folgende Feststellung in Beziehung: Der Ausdruck $\Gamma(s/2)\,\pi^{-s/2}\,\zeta(s)$ „bleibt ungeändert, wenn in 1-s verwandelt wird“, also

$\Gamma(s/2)\,\pi^{-s/2}\,\zeta(s) = \Gamma\bigl((1-s)/2\bigr)\,\pi^{-(1-s)/2}\,\zeta(1-s).$

Näherungsweise Berechnung

Stirlingsche Formel

Näherungswerte der Gammafunktion für x>0 liefert unter anderem die Stirlingsche Formel, es gilt

$\Gamma(x) = \sqrt{2\pi}\,x^{x-1/2}\,\mathrm{e}^{-x}\,\mathrm{e}^{\mu(x)}$ mit $0 < \mu(x) < 1 / (12x).$

Rekursive Näherung

Aus der Funktionalgleichung

$\Gamma(z+1) = z \cdot \Gamma(z),$

die eine Art Periodizität beinhaltet, können aus bekannten Funktionswerten in einem Streifen der Breite 1 in $\operatorname {Re} (z)$ die Werte in jedem anderen entsprechenden Streifen rekursiv berechnet werden. Mit

$\log\Gamma(z) = \log\Gamma(z+1) - \log z$

kann man von einem Streifen auf den benachbarten mit kleinerem Realteil gelangen, und das -fach. Da es für großes |z| sehr gute Näherungen für $\log \Gamma(z)$ gibt, kann deren Genauigkeit in Bereiche übertragen werden, in denen direkte Anwendung der betreffenden Näherung nicht anzuraten wäre. Nach Rocktäschel empfiehlt sich, wie schon von Carl Friedrich Gauß bemerkt, die aus der Stirling-Formel abgeleitete asymptotische Entwicklung in

$\operatorname {Re} (z)={\frac {1}{2}}\log(2\pi )+\left(z-{\frac {1}{2}}\right)\left(\log \left(z-{\frac {1}{2}}\right)-1\right)$ .

Diese hat zwar im Nahbereich bei $z = \tfrac{1}{2}$ eine Irregularität, ist aber schon für |z| > 10 brauchbar. Mit dem Korrekturterm $-\tfrac{1}{24}\left(z-\tfrac{1}{2}\right)^{-1}$ wird ihr Fehler auf die Größenordnung $\mathcal{O}(z^{-3})$ für unbeschränkt wachsendes |z| verringert.

Die -fache Anwendung dieser Näherung führt auf

$\log \Gamma (z)\approx \operatorname {Re} (z+m)-\sum _{k=0}^{m-1}\log(z+k).$

Den komplexen Logarithmus berechnet man über die Polardarstellung von . Für die meisten Anwendungen, etwa in der Wellenausbreitung, sollte m=100 ausreichen.

Unvollständige Gammafunktion

In der Literatur wird dieser Begriff, im Hinblick auf Integrationsgrenzen und Normierung (Regularisierung), nicht einheitlich verwendet.

Häufige Notationen sind:

$\gamma (a,x)=\int _{0}^{x}t^{{a-1}}{\mathrm {e}}^{{-t}}\,{\mathrm d}t$ unvollständige Gammafunktion der oberen Grenze

$\Gamma (a,x)=\int _{x}^{\infty }t^{{a-1}}{\mathrm {e}}^{{-t}}\,{\mathrm d}t$ unvollständige Gammafunktion der unteren Grenze

$\operatorname{P}(a,x) = \frac{\gamma(a,x)}{\Gamma(a)}$ regularisierte (unvollständige) Gammafunktion der oberen Grenze

$\operatorname{Q}(a,x) = \frac{\Gamma(a,x)}{\Gamma(a)}$ regularisierte (unvollständige) Gammafunktion der unteren Grenze

Spricht man von einer regularisierten Gammafunktion, so impliziert dies schon, dass sie unvollständig ist.

$\Gamma (a,x,y)=\int _{x}^{y}t^{{a-1}}{\mathrm {e}}^{{-t}}\,{\mathrm d}t$ oder $\Gamma (a,x,y)={\frac {1}{\Gamma (a)}}\int _{x}^{y}t^{a-1}\mathrm {e} ^{-t}\,\mathrm {d} t$

steht für die verallgemeinerte unvollständige Gammafunktion.

Siehe auch

Literatur

Emil Artin: Einführung in die Theorie der Gammafunktion. B. G. Teubner, Leipzig 1931; The Gamma function. Holt, Rinehart and Winston, New York 1964 (englische Übersetzung von Michael Butler).
Friedrich Lösch, Fritz Schoblik: Die Fakultät (Gammafunktion) und verwandte Funktionen. Mit besonderer Berücksichtigung ihrer Anwendungen. B. G. Teubner, Leipzig 1951.
Konrad Königsberger: Die Gammafunktion. Kapitel 17 in Analysis 1. Springer, Berlin 1990; 6. Auflage 2003, ISBN 3-540-40371-X.

Basierend auf einem Artikel in:

Wikipedia.de